1.Кинематика прямолинейного движения материальной точки. Материальная точка. Система отсчета. Скорость и ускорение. Траектория, путь, перемещение.

Уравнение траектории. Кинематика - раздел физики, изучающий движение тел, не интересуясь причинами, обуславливающие это движение.

Механи́ческое движе́ние - это изменение положения тела в пространстве относительно других тел с течением времени. (механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением)Характеристики механического движения связаны между собой основными кинематическими уравнениями: Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размерами и вращением которого можно пренебречь. Можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки. Практически под материальной точкой понимают обладающее массой тело, размерами, формой и вращением которого можно пренебречь при решении данной задачи Система отсчета: — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. Скорость:  -векторная величина, характеризующая быстроту перемещения частицы по траектории, в который движется эта частица в каждый момент времени. -производная радиуса вектора частицы по времени. -производная от перемещения по времени. Ускорение: -векторная величина, характеризующая быстроту изменения вектора скорости. -производная от скорости по времени.

Траектория - линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. Существенно, что понятие о траектории имеряет физический смысл даже при отсутствии какого-либо по ней движения.

Путь s = f(t). Путь - длина участка траектории материальной точки, пройденного ею за определенное время.

Путь - скалярная величина, характеризующая длинну траектории движения тела. Перемещение - направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение (векторная величина)

2.Кинетатика криволинейного движения материальной точки. Тангенциальное, нормальное и полное ускорение. Формулы расчета нормального и тангенциального ускорения. Принцип относительности и суперпозиции движений. Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции v_xи v_y ее скорости на оси Ox и Oy и координаты x и  y точки в любой момент времени t определяется по формулам         Тангенциальное ускорение — направлено по касательной к траектории. Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю. Центростремительное или Нормальное ускорение — возникает при движении точки по окружности. Является составляющей вектора ускорения a. Вектор нормального ускорения всегда направлен к центру окружности. , где v – мгновенное значение скорости,   r – радиус кривизна траектории в данной точке, Полное ускорение - это корень квадатный из суммы квадратов нормально и тангенцального ускорений. Относительность движения: Положение каждого тела в пространстве всегда рассматривается относительно других тел. Тело может находиться в состоянии покоя относительно одного тела и одновременно - в состоянии движения относительно другого тела. Например, человек, сидящий в кресле летящего самолета,  находится в состоянии покоя относительно самолета,  но одновременно - в состоянии движения относительно земли.  И "виноваты" в этом разные системы отсчета!  В этом и состоит относительность движения. Относительность движения проявляется и в том, что скорость, траектория, пройденный путь и некоторые другие характеристики движения относительны,  т.е. они могут быть различны в разных системах отсчета. Т.к. движение относительно, то задачи в механике можно решать только в условиях определенных выбранной системы отсчета.

Принцип суперпозиции: Если тело выполняет разные движения в разных направлениях, то эти движения могут рассчитываться отдельно и складываться по принципу суперпозиции. Например, если в одной плоскости тело совершает вращательное движение, а по оси, перпендикулярной этой плоскости — равномерное поступательное, то вид движения — винтовая линия с постоянным шагом.

3.Кинематика вращательного движения твердого тела относительно неподвижной оси. Угловое перемещение, угловая скорость и угловое ускорение. Связь между угловыми и линейными кинематическими величинами. Уравнение зависимости угла поворота от времени.

Вращательное движение тела вокруг неподвижной направленной оси — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой хх, называемой осью вращения.

Угловое перемещение — векторная величина, характеризующая изменение угловой координаты в процессе её движения.

Угловая скорость — отношение угла поворота радиус-вектора точки к промежутку времени, за который произошел этот поворот.(направление вдоль оси вокруг которой вращается тело) Частота вращения - физическая величина, измеряемая числом полных оборотов, совершаемых точкой в единицу времени при равномерном движении в одном направлении(n) Период вращения - промежуток времени, в течение которого точка совершает полный оборот,  двигаясь по окружности (T) N – число оборотов, совершаемых телом за время t.  Угловое ускорение - величина, характеризующая изменение с те­чением времени угловой скорости тела. Связь между угловыми и линейными величинами:  связь между линейной и угловой скоростью.  связь между тангенциальным и угловым ускорением.  вязь между нормальным (центростремительным) ускорением, угловой скоростью и линейной скоростью.

При равномерном движении точки по окружности её траекторией является дуга. Точка движется с постоянной угловой скоростью  , а зависимость угла поворота точки от времени является линейной: , где   — начальное значение угла поворота. Эта же формула определяет угол поворота абсолютно твёрдого тела при его равномерном вращении вокруг неподвижной оси, то есть при вращении с постоянной угловой скоростью  . Важной характеристикой данного типа движения является линейная скорость материальной точки  Нужно помнить, что равномерное движение по окружности — движение равноускоренное. Хотя модуль линейной скорости и не меняется, но меняется направление вектора линейной скорости (из-за нормального ускорения)

4.Законы Ньютона. Формулировка первого закона и принцип его действия. Причины изменения скорости тела. Инерциальные и неинерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея. Масса, сила, импульс тела. Формулировка второго закона Ньютона и уравнение движения материальной точки в инерциальной системе отсчета. Третий закон Ньютона и принципы его действия. Инвариантность уравнения движения относительно преобразований Галилея. Первый закон Ньютона называют также законом инерции. Закон звучит так: инерциальные системы существуют. Инерциальной системой называется такая система отсчета, в которой любая материальная точка находится либо в состоянии покоя, либо в состоянии равномерного прямолинейного движения. Закон говорит о том, что инерция существует. Другая формулировка закона инерции: тело, изолированное от внешних воздействий, пребывает либо в состоянии покоя, либо в состоянии равномерного прямолинейного движения. Если на тело не воздействуют никакие силы, оно движется по инерции. Понятие инерциальной системы отсчета – научная абстракция. В реальности таких систем практически нет. Причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу. Первый закон Ньютона утверждает (которое с той или иной степенью точности можно проверить на опыте) о том, что инерциальные системы существуют в действительности. Этот закон механики ставит в особое, привилегированное положение инерциальные системы отсчета. Системы отсчета, в которых выполняется первый закон Ньютона, называют  инерциальными. Инерциальные системы отсчета – это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий илиих взаимной компенсации покоится или движется равномерно и прямолинейно. Неинерциальные системы отсчета – это системы отсчета, в которых наблюдается ускоренное движение тел при отсутствии действия на них сил со стороны других тел. Причина неинерциальности систем отсчета – ускоренное движение этих систем отсчета относительно инерциальной системы. Движение тел в неинерциальных системах отсчета: выполняется второй закон Ньютона, если формально считать, что здесь, кроме реальных сил взаимодействия, существует еще так называемые силы инерции. Принцип относительности Галилея, который утверждает то же самое, но не для всех законов природы, а только для законов классической механики, подразумевая применимостьпреобразований Галилея и оставляя открытым вопрос о применимости принципа относительности к оптике и электродинамике. Преобразования Галилея – название преобразований в классической механике, согласно которым изменяются значения физических величин при переходе между различными инерционными системами отсчета.  Преобразования Галилея позволяют описать физическое явление в инерциальной системе отсчета если известно как выглядит данное физическое явление в другой инерциальной системе отсчета.  Если оси координат в двух системах отсчета имеют одинаковые направления, а одна система движется вдоль оси y второй системы с постоянной скоростью V, то преобразование имеют вид:  Соответственно меняются компоненты скорости  Другие величины, такие как ускорение, сила, масса при преобразованиях Галилея не меняются. Соответственно, не изменяется вид уравнений Ньютона. Говорят, что уравнение Ньютона инвариантны относительно преобразований Галилея. 

Масса- физическая величина, являющаяся мерой инерционных ( инертная масса ) и гравитационных ( гравитационная масса ) свойств тела называется инертной массой этого тела. В этом смысле масса выступает как свойство тел не поддаваться изменению скорости как по величине, так и по направлению. Инертная и гравитационная массы равны друг другу. Сила тяжести пропорциональна массе тела, на которое она действует  P=mg; Если тело покоится, то вес тела равен силе тяжести, на него действующей, и в формуле (1) можно считать Р весом тела. Значит, для покоящихся тел их веса пропорциональны массам, так что для двух тел с массами m1  и m2 и весами Р1 и Р2 справедливо равенство Сила- векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры (деформируется). В каждый момент времени сила характеризуется величиной, направлением в пространстве и точкой приложения.

Сила характеризуется числовым значением,  направлением  в  пространстве и точкой приложения. Единица силы – ньютон. 1 Н = кг 5. 0м/с 52 0.

Импульс тела р – физическая величина, равная произведению массы тела на его скорость: p=mV Закон сохранения импульса – для системы, состоящей из любого числа тел, суммарный импульс системы остается постоянным, при условии, что внешние силы отсутствуют. отсюда находим: Второй Закон Ньютона: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. Обычно этот закон записывается в виде формулы: где   — ускорение тела,   — сила, приложенная к телу, а   — масса материальной точки. Или, в ином виде: Уравнение движения материальной точки в инерциальной системе отсчета: Физический смысл производной : если точка движется вдоль оси x и ее координата изменяется по закону S(t),  то мгновенная скорость точки находиться по формуле v(t)=lim t 0 tS(t+ t)−S(t)=S (t), а ускорение по формуле a(t)=lim t 0 tv(t+ t)−v(t)=v (t)=S (t) Итак:

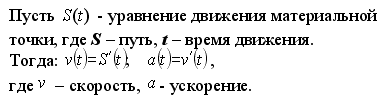
Третий закон Ньютона и принципы его действия: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно. Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону. Инвариантность уравнений движения относительно преобразований Галилея представляет собой математическую формулировку принципа относительности классической механики: законы дви жения одинаковы во всех системах координат, равномерно движущихся относительно друг друга. Первый постулат теории относительности согласуется с этим принципом и обобщает его на законы распространения света. Однако одновременное применение обоих постулатов находится в противоречии с преобразованиями Галилея. Самый факт инвариантности уравнений движения по отношению к преобразованиям Галилея называют иногда принципом относительности Галилея.

5.Силы в механике. Классификация сил в природе. Закон всемирного тяготения. Физический смысл гравитационной постоянной. Сила тяжести и вес тела. Упругие силы, закон Гука. Сила трения и сопротивления. Сложение сил. Классификация сил в природе.: Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона  можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях. Закон всемирного тяготения Силу взаимного притяжения, действующую между Солнцем, планетами, кометами, звездами и другими телами во Вселенной, Ньютон назвал силой всемирного тяготения.Сила всемирного тяготения, действующая на Луну со стороны Земли, пропорциональна массе Луны (см. формулу 9.1). Очевидно, что сила всемирного тяготения, действующая со стороны Луны на Землю, пропорциональна массе Земли. Эти силы по третьему закону Ньютона равны между собой. Следовательно, сила всемирного тяготения, действующая между Луной и Землей, пропорциональна массе Земли и массе Луны, т. е. пропорциональна произведению их масс. Распространив установленные закономерности — зависимость силы тяжести от расстояния и от масс взаимодействующих тел — на взаимодействие всех тел во Вселенной, Ньютон открыл в 1682 г. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними: Силы всемирного тяготения называют гравитационными силами, а коэффициент пропорциональности G в законе всемирного тяготения называют гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.  По современным данным она равна . Физический смысл гравитационной постоянной:  гравитационная постоянная численно равна модулю силы тяготения, действующей между двумя точечными телами массой по 1 кг каждое, находящимися на расстоянии 1 м друг от друга. Из этого утверждения следует, что гравитационная постоянная является просто коэффициентом для согласования размерностей. Сила тяжести и вес тела  Сила тяжести. Силой тяжести тела массой m называется сила притяжения его к Земле F=mg, g-ускорение свободного падения. Вследствие суточного вращения Земли и несферичности ее формы величина g различается от 9,78 м/с² на экваторе до 9,83 м/с² на полюсах. В среднем на поверхности Земли =9,8 м/с² , M и R - масса и радиус Земли. На высоте h над поверхностью Земли Вес тела: Вес представляет собой силу, с которой тело действует на горизонтальную опору или на подвес. По величине вес и сила тяжести совпадают только в том случае, если опора неподвижна. Например, вес тела, находящегося в движущемся вверх с ускорением лифте, превышает его силу тяжести. Упругие силы, закон Гука   Упругие силы Электромагнитные силы в механике проявляют себя как упругие силы и силы трения. Под действием внешних сил возникают деформации (т.е. изменение размеров и формы) тел. Если после прекращения действия внешних сил восстанавливаются прежние форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, называемого пределом упругости.При превышении этого предела деформация становится пластичной, или неупругой, т.е. первоначальные размеры и форма тела полностью не восстанавливаются. Сила упругости, действующая на тело со стороны деформированной (сжатой или растянутой) пружины, равна по величине , k- коэффициент упругости (жесткость) пружины, x - величина деформации пружины. Закон Гука Формулировка: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации. Для тонкого растяжимого стержня закон Гука имеет вид:

, здесь F — сила, которой растягивают (сжимают) стержень,   — абсолютное удлинение (сжатие) стержня, а k — коэффициент упругости (или жёсткости). Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L) явно, записав коэффициент упругости как .

Величина E называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала. Если ввести относительное удлинение и нормальное напряжение в поперечном сечении , то закон Гука для относительных величин запишется как В такой форме он справедлив для любых малых объёмов материала.Также при расчёте прямых стержней применяют запись закона Гука в относительной форме Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Сила трения и сопротивления Сила трения. При скольжении тела действующая на него сила трения , k - коэффициент трения, N - сила реакции опоры (рис. 4 ).

Сила сопротивления: Силу, которая противодействует первоначальному сдвигу предмета, называют силой трения покоя. Хотя нагляднее её называть силой сопротивления. Именно сила сопротивления является необходимым условием для изменения скорости тела, т.е. для начала движения или для начала торможения. Это как необходимость воздуха для дыхания (условие необходимое, но не достаточное). В процессе движения мы толкаем Землю, а она толкает нас.Если приложенная сила не достаточно велика, то сила сопротивления её уравновешивает. Затем сила сопротивления достигает своего максимума, и тело начинает движение, т.е.F _{сопротивления макс.} > F _{тр. скольжения}.