2.3 Классическая интерпретация эпр

Допустим, что парамагнитные свойства образца определяются магнитными моментами µ_i входящих в него частиц, например магнитных моментов неспаренных электронов парамагнитных атомов или молекул. При отсутствии внешнего магнитного поля магнитные моменты отдельных парамагнитных частиц ориентированы хаотически, поэтому суммарный магнитный момент образца равен нулю. Во внешнем магнитном поле Н₀ образец намагничивается, то есть возникает неравный нулю суммарный магнитный момент М, ориентированный по направлению поля.

Поведение магнитного момента М во внешнем магнитном поле H₀ можно уподобить движению магнитного волчка, имеющего механический момент количества движения J. Магнитный момент волчка пропорционален его механическому моменту: М = γJ (в случае электрона векторы М и J ориен­тированы в противоположные стороны, то есть γ< 0). В магнитном поле Н₀ на волчок действует вращательный момент, определяемый векторным произ­ведением [М(t) х Н₀]. Уравнение движения магнитного момента М в постоянном магнитном поле Н₀ имеет вид

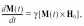
где γ— отношение магнитного момента к механическому. Из этого уравнения следует, что магнитный момент М будет прецессировать (совершать круго­вые вращения) вокруг вектора Н₀ с круговой часто­той ω_L = -γН₀. Это явление называется ларморовской прецессией (рис. 2).

Допустим теперь, что помещенный в постоянное магнитное поле Н₀ образец облучается сравнительно слабым переменным электромагнитным полем, у которого вектор магнитного поля Н₁(t) перпендикулярен постоянному магнитному полю Н₀ (Н₁﬩ Н₀ и |Н₁|«|Н₀|). Допустим также, что переменное поле Н₁(t) поляризовано по кругу, то есть вектор Н₁(t) вращается в плоскости xy с круговой частотой ( ω₁ = = 2πν₁ (рис. 2). Это значит, что теперь на магнитный момент М будет действовать дополнительный вращательный момент [М(t)xH₁(t)], создаваемый переменным магнитным полем. Если частота элект­ромагнитного излучения ( ω₁ сильно отличается от частоты ларморовской прецессии ( ω_L, то переменное поле не будет оказывать существенного влияния на прецессию вектора М. В этом случае разность фаз между векторами М(t) и Н₁(t) непосто­янна, поэтому среднее по времени значение дополнительного вращательного момента [М(t) х Н₁(t)] будет равно нулю. Однако по мере приближения частоты переменного электромагнитного поля ю ω₁ к частоте ларморовской прецессии ( ω_L влияние переменного поляН₁(t) на движение вектора М будет становиться заметнее. При совпадении частот ( ω₁ и ω_L векторы М(t) и Н₁(t)) будут вращаться синхронно. Это значит, что в условиях резонанса (ω₁ = ω_L) абсолютная величина дополнительного вращательного момента [М(t) х Н₁(t)] будет постоянна и всегда отлична от нуля. Поэтому даже слабое переменное поле Н₁(t)может существенно влиять на прецессию вектора намагниченности М(t). Под действием переменного поля Н₁(t) угол прецессии θ станет периодически изменяться: вектор намагниченности М(t) будет то приближаться к плоскости xy, то удаляться от нее (рис. 2).

Как мы отмечали выше, энергия магнитного момента М во внешнем магнитном поле зависит от его ориентации, E = - (М • Н) = -| М | • | Н | cosθ. Откло­нение вектора намагниченности М(t) от оси z (уве­личение угла прецессии θ) отвечает увеличению энергии парамагнетика, которое происходит за счет поглощения энергии переменного магнитного поля Н₁(t). Приближение вектора М(t) к оси z (уменьшение угла θ) сопровождается понижением энергии магнитного момента М, которая будет выделяться в форме электромагнитного излучения с резонансной частотой ω_рез = ω_L. Таким образом, если отвлечься от процессов магнитной релаксации, то оказывается, что в течение полупериода, когда вектор М(t) приближается по направлению к вектору внешнего магнитного поля Н₀, энергия переменного магнитного поля будет излучаться образцом, а во время следующего полупериода — поглощаться. Поэтому, казалось бы, в целом парамагнитный образец не должен поглощать энергию электромагнитного излучения. Однако спины могут без излучательно (в виде тепла) отдавать поглощаемую ими энергию решетке, в результате чего резонансное по­глощение энергии будет преобладать над излучени­ем. Так можно объяснить явление ЭПР в рамках классической (не квантовой) физики.

Заметим, что условием резонансного поглощения энергии электромагнитного излучения является не только равенство частот ω₁ и ω_L, но и совпадение направления круговой поляризации переменного поля Н₁(t) с направлением прецессии вектора намагниченности М(t) в поле Н₀. На практике пользуются линейно поляризованным электромагнитным излучением, которое всегда можно представить в виде суперпозиции двух излучений одинаковой частоты, поляризованных по кругу, но вращающихся в разные стороны. Спектрометры ЭПР устроены так, что с образцом взаимодействует только правильно поляризованная компонента.

Основой метода ЭПР является резонансное поглощение электромагнитного излучения системой неспаренных электронов при ее переходе между двумя дискретными энергетическими уровнями. Дискретные уровни энергии образуются за счет эффекта Зеемана, который описывает взаимодействие магнитного момента электрона m с внешним магнитным полем с индукцией В.

Е = <µВ> = µВcosβ (2.7)

где Е - энергия взаимодействия, <µВ> - векторное , а (µВ) скалярное произведение магнитного момента электрона и индукции внешнего магнитного поля, cosβ - косинус угла между этими двумя векторами, что позволяет считать произведение µcosβ проекцией µ на В.

Электрон, обладая собственным моментом количества движения (спином) S, имеет магнитный момент:

µ_s = g • S (2.8)

где g = µ_S /S, (g - же фактор, или фактор спектроскопического расщепления, который для свободного электрона составляет 2,0023193).

В отсутствии внешнего магнитного поля любые ориентации вектора магнитного момента электрона в пространстве равновероятны, т.е. имеют одинаковое значение энергии Е₀. Говорят, что энергетические уровни вырождены. При наложении внешнего магнитного поля с индукцией В магнитный момент электрона может иметь лишь две разрешенные ориентации, соответственно две проекции на направление внешнего поля. Они характеризуются с помощью магнитного квантового числа m и равны +1/2 и -1/2.

Энергию взаимодействия магнитного момента электрона с внешним магнитным полем с учетом (1) и (2) можно записать как:

Е = mgµ_ВB , (2.9)

где µ_В - магнетон Бора, единица электронного магнетизма. Магнетон Бора дается выражением: µ_В = е • h / 2m_е и составляет с системе СИ 9,2741 • 10^-24 Дж/Тл, если е - заряд электрона (1,6021 • 10^-19 К), а m_е - масса покоя электрона (9,1091 • 10^-31 кг).

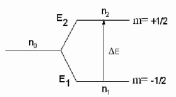
При разной ориентации магнитного момента электрона: «по полю» (m = -1/2) и «против поля» ( m = +1/2) возникают два уровня энергии Е₁ и Е₂, происходит расщепление энергетического уровня Е₀ на два с меньшей (Е₁= -1/2 gµ_ВB ) и большей (Е₂ = +1/2 gµ_ВB) энергией.

Тогда разница в энергетических уровняхΔ Е, равная Е₂ - Е₁ выразится как:

Δ Е = g|µв B, (2.10)

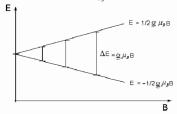
она зависит от величины магнитного момента электрона m = gтв и магнитной индукции внешнего магнитного поля В (рис.7 ).

Количество неспаренных электронов (спинов) на верхнем и нижнем энергетическом уровнях будет различным, т.е. заселенность нижнего энергетического уровня (n₁) будет больше, чем верхнего (n₂ ), поскольку любая система стремится к минимуму энергии, n₁>n₂ . Различие в заселенностях уровней можно найти из распределения частиц по энергиям Больцмана:

n₁ / n₂ ~ exp( -ΔE/kT) (2.11)

При комнатной температуре и внешнем поле 0,3 Т отношение заселенностей составляет 1,00016, т.е близко к единице. Причиной является тот факт, что ΔE<<kT( разность зеемановских уровней энергии, т.е. ΔE, составляет ~ 1 Дж/моль, что значительно меньше средней энергии теплового движения частиц ~ 2500 Дж/моль).

a)

b)

Рис. 7. Расщепление электронного уровня Е₀ во внешнем магнитном поле (а) и зависимость величины расщепления ΔE от магнитной индукции В внешнего поля (б).

Тем не менее, большая заселенность нижнего энергетического уровня является причиной появления сигнала электронного парамагнитного резонанса (ЭПР).

Если на такую систему различным образом ориентированных спинов ( m = +1/2 и m = - 1/2) направить поток электромагнитного излучения с энергией квантов hv = Δ Е, то будет происходить поглощение интенсивности излучения (I) и прибор зафиксирует сигнал. Уравнение, которое отражает ____ условия резонанса

hv = ΔE = gµ_BB (2.12)

можно считать основным уравнением электронного парамагнитного резонанса.

Достичь резонанса, можно двумя путями: менять частоту излучения v при постоянном внешнем поле (В₀ = const), или изменять индукцию поля В при постоянной частоте электромагнитного излучения (v₀ = const). Второй путь технически более простой, он и реализуется на практике.