1 билет

Общие понятия о множествах. Объединение пересечение, диаграммы Венна

Множеством - называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое \целое.  Отдельные объекты, из которых состоит множество, называются элементами множества. Множества принято обозначать большими буквами латинского алфавита, а элементы этих множеств — маленькими буквами латинского алфавита. Множества записываются в фигурных скобках { }. Множества бывают конечные и бесконечные. Множества называются конечным, если число его элементов конечно, т.е. если существует натуральное число n, являющееся числом элементов множества. А={a1, a2,a 3, ..., an}. Множество называется бесконечным, если оно содержит бесконечное число элементов. B={b1,b2,b3, ...}. Например, множество букв русского алфавита — конечное множество. Множество натуральных чисел — бесконечное множество.

2 Билет

Теоремы сложения и умножения

Теорема 1 (принцип сложения). Пусть A B =  . Тогда n(A B) = n(A) + n(B).

Следствие 2. Пусть A₁, A₂….A_l – система попарно непересекающихся конечных множеств.

Тогда n(A₁  A₂  …  A_l) = n(A₁)+n(A₂)+…+n(A_l).

Доказательство. При l=2 мы ссылаемся на теорему 1:

n(A₁  A₂) = n(A₁) + n(A₂).

Допустим, что утверждение верно при l = k, то есть

n(A₁  A₂  …  A_k) = n(A₁) + n(A₂) +…+ n(A_k).

Докажем утверждение при l = k+1.  В этом случае

 n(A₁  A₂  …  A_k  A_k+1) = n((A₁  A₂  …  A_k)   A_k+1) = n(A₁  A₂  …  A_k) + n(A_k+1). Здесь мы воспользовались базисом индукции и, применяя индуктивное предположение, получим:

n(A₁ A₂  …  A_k) + n(A_k+1) = n(A₁) +…+ n(A_k) + n(A_k+1).

 Следствие доказано.

Иногда принцип сложения, применительно к задачам комбинаторики, можно встретить в таком виде: если объект x можно получить m способами, а объект y можно получить l способами, причем множества этих способов не пересекаются, то объект x или объект y можно получить m + l способами. Таким образом, необходимо помнить, что в комбинаторике союз “или” ассоциирован с операцией сложения.

Теорема 3 (принцип умножения). Если множество A состоит из m элементов, а множество B состоит из l элементов, то n(A B) =ml.

Доказательство. Будем доказывать методом математической индукции по l. При l=1 множество B состоит из одного элемента: B={b₁}. Поэтому множество A B={(a_i, b₁)|i =1, 2,…,m} состоит из m элементов, то есть n(A B)=m · 1=m · l. Базис индукции проверен.

        Допустим, утверждение верно при l = k, то есть, если n(A) = m, n(B) = k, то n(A B) = m · k. Докажем утверждение при l = k + 1. Пусть B = {b₁, b₂ ,…, b_k , b_k+1} или B =  B^' {b_k+1}, где множество B^' = {b₁, b₂ ,…, b_k} состоит из kэлементов. По индуктивному предположению n(A  B^') = n(A) · n(B^') = m · k. С другой стороны

B = B^' {b_k+1}, поэтому (A B) = A   B^'  A      {b_k+1}, причем

A   B^'   A   {b_k+1} =  , так как B^'   {b_k+1} =  . По теореме 1 n(A B) = n(A   B^'  A   {b_k+1}) = n(A   B^') + n(A   {b_k+1})= =m · k + m · 1 = m(k +  1) = m · l. Теорема доказана.

В комбинаторном изложении принцип умножения часто формулируют так: если объект x можно сконструировать m способами, объект y можно сконструировать l способами, то объект (x, y) или (x и y) можно сконструировать m · l способами. То есть союз “и” в комбинаторики ассоциирован с операцией умножения.

3 Билет

Формула включений исключений

Формула включений-исключений (или принцип включений-исключений) — комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом. В теории вероятностей аналог принципа включений-исключений известен как формула Пуанкаре.

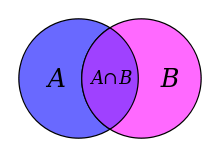
Случай двух множеств

Например, в случае двух множеств   формула включений-исключений имеет вид:

В сумме   элементы пересечения   учтены дважды, и чтобы компенсировать это мы вычитаем   из правой части формулы. Справедливость этого рассуждения видна из диаграммы Эйлера-Венна для двух множеств, приведенной на рисунке справа.

Таким же образом и в случае   множеств процесс нахождения количества элементов объединения   состоит во включении всего, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Отсюда и происходит название формулы.