III. Выборочный метод в статистике

3.1. Ошибки выборки

- дисперсия признака х в выборочной совокупности;

w – доля единиц, обладающих исследуемым признаком;

n – объём выборочной совокупности;

N – объём генеральной совокупности;

- выборочная средняя;

- генеральная средняя;

t – коэффициент доверия, который определяется в зависимости от того, с какой вероятностью надо гарантировать результаты выборочного наблюдения.

Задача 7. В случае случайного повторного отбора было установлено, что средний вес товара в выборочной совокупности, состоящей из 100 изделий, оказался равным 10 кг, при среднем квадратическом отклонении 0,6 кг. С вероятностью, равной 0,954, определить в каких пределах заключён средний вес товара в генеральной совокупности.

По условию задачи имеем: Ф_(t)=0,954,

следовательно t=2.

Последовательность расчёта

1. Определим среднюю и предельную ошибки выборки:

2. Средний вес изделия в генеральной совокупности колеблется в пределах:

Таким образом, с вероятностью 0,954 можно утверждать, что средний вес товара в генеральной совокупности колеблется в пределах от 9,88 до 10,12 кг.

3.2. Механическая выборка

Задача 8. Из 1000 таможенных работников в порядке механической выборки отобрано 100 работников в целях изучения их среднего стажа работы. Определить: 1) с вероятностью 0,954 средний стаж таможенных работников; 2) с вероятностью 0,997 долю таможенных работников со стажем свыше 20 лет и пределы генеральной совокупности.

Стаж, годы, Х	Число таможенных работников, f	Середина интервала, Хi	Xif	Xi2	Xi2f
0-5	6	2,5	15	6,25	37,5
5-10	12	7,5	90	56,25	675
10-15	18	12,5	225	156,25	2812,5
15-20	30	17,5	525	306,25	9187,5
20-25	20	22,5	450	506,25	10125
Свыше 25	14	27,5	385	756,25	10587,5
	∑f=100		∑=1690		∑=33425

Порядок расчёта

1. Рассчитываем среднюю арифметическую выборочной совокупности:

2. Рассчитываем дисперсию выборочной совокупности:

3. Определим среднюю ошибку механической выборки:

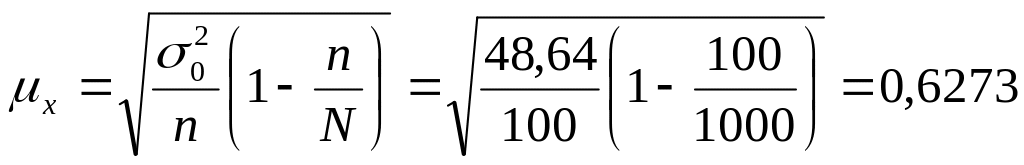
4. Предельная ошибка механической выборки:

Так как вероятность 0,954 t=2, следовательно,

5. Вычисляем пределы, в которых находится средняя арифметическая в генеральной совокупности:

, 16,9 – 1,2≤ х ≤16,9 + 1,2

15,7≤ х ≤18,1

С вероятностью 0,954 можно утверждать, что средний стаж работников в генеральной совокупности находятся в пределах от 15,7 до 18,1 года.

6. Доля таможенных работников, стаж которых свыше 20 лет, в выборочной совокупности составит:

w=m/n=34/100=0,34,

где m – число таможенных работников со стажем свыше 20 лет в выборочной совокупности;

n – число таможенных работников в выборке.

7. Определяем среднюю ошибку механической выборки для доли:

8. Предельная ошибка доли:

Так как при вероятности 0,997 t=3, следовательно,

9. Определяем пределы, в которых находится доля (число работников со стажем свыше 20 лет) в генеральной совокупности:

, 0,34 – 0,135≤ p≤ 0,34+0,135

0,205≤ p≤0,475

С вероятностью 0,997 можно утверждать, что доля таможенных работников со стажем свыше 20 лет в генеральной совокупности не менее 20,5% и не менее 47,5%.