2. Типы алгоритмов

Традиционно процесс решения задачи на компьютере складывается из таких этапов:

- постановка задачи, т.е. четкая ее формулировка с определением цели, которую необходимо достичь. Здесь выделяются начальные данные, результаты и определяется связь между начальными данными и результатами;

- создание математической модели, т.е. определения математических соотношений (формулы, уравнения и т.д.), что связывают результаты с начальными данными;

- разработка алгоритма решения задачи, т.е. построение схемы (набора инструкций) этого процесса;

• написание программы на языке программирования;

• отладка программы, т.е. поиск ошибок в программе и устранение их;

• тестирование программы, т.е. решение задачи на компьютере и анализ

полученных результатов.

В различных задачах некоторые из этапов могут отсутствовать, а некоторые этапы могут быть разделены на большее число, при этом описание алгоритма и механизм и его реализации – конечны.

Рассмотрим повторно тот же алгоритм Евклида несколько в другой интерпретации (операция вычитания, вместо деления) и более строгий способ его словесной записи.

Пример 2.1. Алгоритм Евклида (НОД).

1. Начало.

2. Ввести целые числа M и N.

3. Если M = N, то перейти на шаг 7, иначе – на шаг 4.

4. Если M < N, то перейти на шаг 5, иначе – на шаг 6.

5. Уменьшить N на значение M (N-M), перейти на шаг 3.

6. Уменьшить M на значение N (M-N), перейти на шаг 3.

7. Принять за НОД значение M.

8. Конец.

Это пример числового алгоритма, который сводит решение приведенной задачи до арифметических действий над числами. Существует другой тип алгоритмов, которые содержат указания обработки (команды) не чисел, а объектов любой природы. Это логические и эвристические алгоритмы.

Рассмотрим пример логического алгоритма.

Пример 2.2. Типовым примером логического алгоритма является алгоритм поиска пути в конечном лабиринте. Лабиринт удобно изобразить в виде графа, где вершины – это площадки лабиринта, дуги – его коридоры. Необходимо выяснить, достижима ли площадка f из начальной площадки a, если это так, то найти путь с a в f, если же нет, то вернутся в a.

Пусть человек, который ищет путь в лабиринте, имеет в своем распоряжении клубок ниток, конец которой закреплен в a, и, двигаясь по лабиринту, может разматывать клубок (Р ) или, наоборот, наматывать (Н) на него нитку.

Можно делать отметки на проходных коридорах и различать потом их: ни разу не пройденные (З – зеленные), пройденные один разу (Ж – желтые), пройденные дважды (К – красные). Метод поиска можно задать такой схемой:

1. площадка f – остановка (цель достигнута);

2. петля (П) – наматываем нитку (от площадки расходятся, по крайней мере, два желтых коридора);

3. зеленая улица (ЗУ) – разматываем нитку (от площадки выходит, по крайней мере, один зеленный коридор);

4. площадка а – остановка (начальный пункт);

5. отсутствие всех предыдущих признаков (ОП) – наматываем нитку.

Очутившись на некоторой площадке, необходимо свериться со схемой признаков в указанном порядке и сделать очередной ход относительно первого выявленного признака, не проверяя других признаков до тех пор, пока не настанет остановка. Один из возможных вариантов поиска пути в лабиринте (рис. 2.1) содержит ходы, приведенные в табл. 2.1. Если пересчитать коридоры, которые остались желтыми (ab, bc, cd, df), то получим путь от a до f.

c

a b g

h

d

f e

Рис. 2.1.

Табл. 2.1.

№ хода	Признак	Ход	Пройденный коридор	Цвет коридора после его прохождения
1	ЗУ	Р	Ab	Ж
2	ЗУ	Р	Bc	Ж
3	ЗУ	Р	Cd	Ж
4	ЗУ	Р	Dg	Ж
5	ЗУ	Р	Gh	Ж
6	ОП	Н	Hg	К
7	ОП	Н	Gd	К
8	ЗУ	Р	Db	Ж
9	П	Н	Bd	К
10	ЗУ	Р	Df	Ж

Пример 2.3. Примером логического алгоритма также является алгоритмы построения выигрышной стратегии для определенного класса игр. Выигрышная стратегия - это набор правил, следуя которым один из игроков обязательно выигрывает. Этот класс игр можно определить так:

1. Двое игроков ходят по очереди.

2. Обязательно выигрывает только один.

3. При выборе очередного хода случайность отсутствует.

4. Каждый играющий знает свои ходы и ходы противника.

Примером такой игры может служить игра “чет-нечет”. Есть шесть предметов и два игрока: А и В. Игрок может за один ход взять от 1 до 2 предметов. Проигрывает тот, кто берет последний предмет. Может ли А, который всегда начинает, “заставить” В взять последний предмет? Оказывается – да, может! Его выигрышная стратегия очень проста: первым ходом он всегда берет два предмета; если число оставшихся предметов не 0 и В взял k (k=1,2) предметов, то А должен взять 3-k предметов. (Проверьте этот факт пока экспериментально).

Первый вопрос, который здесь возникает, как представить игру? До сих пор мы имели дело лишь с числами. Нам же необходимо такое представление игры, которое бы позволило проанализировать все возможные комбинации ходов и найти характерные признаки только тех, которые ведут к победе А.

Воспользуемся для представления игры объектом, который в математике называется двоичное дерево. Двоичное дерево состоит из вершин и дуг, соединяющих вершины. У всех вершин, за исключением одной, есть только одна дуга, “заходящая” в эту вершину, и две дуги, “исходящие” из этой вершины. Единственная вершина, в которую “не заходит” ни одна дуга, называется корнем дерева; вершины, из которых “не исходит” ни одной дуги, называются листьями.

Тогда игру “чет-нечет” для шести предметов в виде дерева можно представить так, как показано на рисунке 2.2.

Здесь каждая вершина представляет состояние в игре, после очередного хода. Каждый ход представлен дугой. Число на дуге показывает, сколько всего предметов было взято в игре с учетом этого хода. Конечные вершины, из которых не исходит ни одной дуги и которые называются листьями, помечаются “+”, если выигрывает А и “-” если  - В.

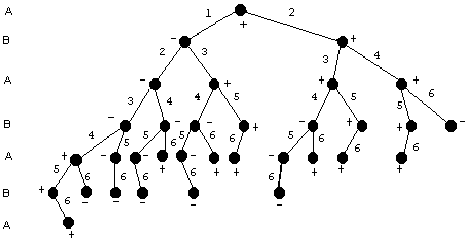
Рис.2.2. Дерево игры “чет-нечет” для шести предметов

Пометим все вершины в этом дереве “+” или “-” по следующему правилу:

1. Если ход А заканчивается хотя бы одним “+”, то помечаем вершину, с которой начинается ход А, так же “+”. В противном случае помечаем вершину, с которой начинается ход А ,“-“.

2. Если ход В заканчивается так, что обе вершины помечены “+”, то вершина, с которой начинается этот ход, так же метится “+”. В противном случае ставим “-”.

Ясно, что если в результате этой разметки корень будет помечен “+”, то есть такая последовательность ходов когда А обязательно выигрывает.

Приведем разновидность этой игры, когда есть 12 предметов и два игрока: А и В. Игрок может за один ход взять от 1 до 3 предметов. Проигрывает тот, кто берет последний предмет. Выигрышная стратегия для игрока А: первым ходом он всегда берет три предмета; если число оставшихся предметов не 0 и В взял k (k=1,2,3) предметов, то А должен взять 4-k предметов. (Проверьте этот факт экспериментально).

Под эвристическими понимаются методы, правильность которых не доказана. Иногда не удается построить контрпример, демонстрирующий ошибочность или неуниверсальность метода. Но не удается доказать математическими средствами и правильность метода. Тем не менее, практика использования эвристических методов дает положительные результаты.

    Эвристические методы разнообразны, поэтому нельзя описать какую-то общую схему разработки таких методов. Чаще всего эвристические методы применяют совместно с методами перебора для сокращения количества проверяемых вариантов: некоторые подмножества вариантов согласно выбранной эвристике считаются заведомо неприемлемыми и не проверяются. Таким образом, переборный алгоритм с эвристикой выполняется гораздо быстрее, чем алгоритм полного перебора. Платой за это является отсутствие гарантии правильности решения или гарантии того, что из всех возможных выбрано наилучшее решение.

    В качестве примеров можно привести задачи выбора наилучшего хода при игре в шахматы или раскраски вершин графа. Например, раскрасить вершины графа таким образом, чтобы смежные вершины были раскрашены в различные цвета, а количество использованных в графе красок было минимальным.