§ 3 Уравнение Эйнштейна для внешнего фотоэффекта. Работа выхода

В 1905 году А. Эйнштейн объяснил фотоэффект на основании квантовых представлений. Согласно Эйнштейну, свет не только испускается квантами в соответствии с гипотезой Планка, но распространяется в пространстве и поглощается веществом отдельными порциями - квантами с энергией E₀ = hv. Кванты электромагнитного излучения называютсяфотонами.

Уравнение Эйнштейна (закон сохранения энергии для внешнего фото­эффекта):

Энергия падающего фотона hv расходуется на вырывание электрона из металла, то есть на работу выхода А_вых, и на сообщение вылетевшему фотоэлектрону кинетической энергии  .

Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого тела в вакуум называется работой выхода.

Так как энергия Ферм к Е_F зависит от температуры и Е_F, также изменяется при изменении температуры, то, следовательно, А_вых зависит от температуры.

Кроме того, работа выхода очень чувствительна к чистоте поверхности. Нанеся на поверхность пленку (Са, Sг, Ва) на W А_вых уменьшается с 4,5 эВ для чистого W до 1,5 ÷ 2 эВ для примесного W.

Уравнение Эйнштейна позволяет объяснить вcе три закона внешнего фо­тоэффекта,        

1-й закон: каждый квант поглощается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интен­сивности (Ф) света

2-й закон: V_max ~ ν и т.к. А_вых не зависит от Ф, то и V_max не зависит от Ф

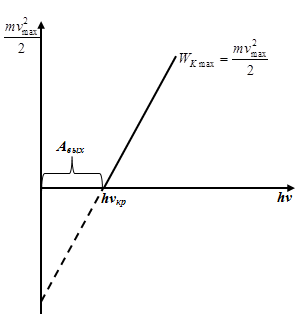
3-й закон: При уменьшении ν уменьшается V_max и при ν = ν₀  V_max = 0, следовательно, hν₀ = А_вых, следовательно,   т.е. существует минимальная частота, начиная с которой возможен внешний фотоэффект.

Фотон - элементарная частица, которая всегда (в любой среде!) движется со скоростью света с и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и нейтрон, которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

Импульс фотона р_g получим, если в общей формуле теории относительности положим массу покоя фотона m_0g = 0:

 

 Рассеяние излучения на свободных электронах

Рассмотрим движение электрона в плоской электромагнитной волне:  , распространяющейся вдоль оси  . Уравнение движения электрона:

и энергия, излучаемая таким электроном,

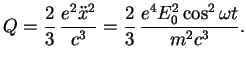
Своих источников энергии у электрона нет. Фактически он переизлучает (рассеивает) энергию падающей электромагнитной волны в других направлениях, так что

эрг с

где  эрг см  -- поток падающей энергии:

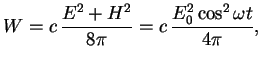
и сечение рассеяния

см

знаменитая формула Томсона. Величина

см

называется классическим радиусом электрона.

При преобладающей роли электронного рассеяния (процессы поглощения излучения несущественны) изменение интенсивности   в монохроматическом пучке фотонов, очевидно, равно

Можно ввести коэффициент ``поглощения'' при томсоновском рассеянии (хотя реально поглощения энергии и нет):

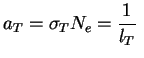см

где длина пробега

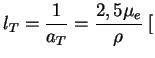см

Интегрируя уравнение для  , получаем

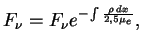
т.е.  г/см  водородной плазмы ( ) уменьшают   в   раз за счет электронного рассеяния.

Теория эффекта Комптона[править | править исходный текст]

Иллюстрация к эффекту Комптона. Излучение с длиной волны   направлено слева направо. После взаимодействия с электроном оно меняет длину волны на  , а направление на угол  относительно первоначального направления. Стрелкой указано направление движения электрона, с которым провзаимодействовал фотон.

При рассеянии фотона на покоящемся электроне частоты фотона   и   (до и после рассеяния соответственно) связаны соотношением:

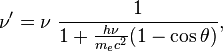
где   — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

где   — комптоновская длина волны электрона, равная   м.

Уменьшение энергии фотона в результате комптоновского рассеяния называется комптоновским сдвигом. Объяснение эффекта Комптона в рамках классической электродинамики невозможно, так как рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не меняет её частоты.

Эффект Комптона является одним из доказательств справедливости корпускулярно-волнового дуализмамикрочастиц и подтверждает существование фотонов.

Закон сохранения энергии в случае эффекта Комптона можно записать следующим образом^[1]:

где   — релятивистская масса электрона, выражаемая через его скорость   следующей формулой:

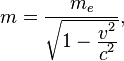
Сечение эффекта Комптона описывается формулой Клейна-Нишины.

Тормозное рентгеновское излучение

Электрон, движущийся в некоторой среде, теряет свою скорость. При этом возникает отрицательное ускорение. Согласно теории Максвелла, любое ускоренное движение заряженной частицы сопровождается электромагнитным излучением. Излучение, возникающее при торможении электрона в веществе анода, называют тормозным рентгеновским излучением.

Свойства тормозного излучения определяются следующими факторами.

1. Излучение испускается отдельными квантами, энергии которых связаны с частотой формулой (26.10)

где ν - частота, λ - длина волны.

2. Все электроны, достигающие анода, имеют одинаковую кинетическую энергию, равную работе электрического поля между анодом и катодом:

где е - заряд электрона, U - ускоряющее напряжение.

3. Кинетическая энергия электрона частично передается веществу и идет на его нагревание (Q), а частично расходуется на создание рентгеновского кванта:

4. Соотношение между Q и hv случайно.

В силу последнего свойства (4) кванты, порожденные различными электронами, имеютразличные частоты и длины волн. Поэтому спектр тормозного рентгеновского излучения является сплошным. Типичный вид спектральной плотности потока рентгеновского излучения (Φ_λ = άΦ/άλ) показан на рис. 32.2.

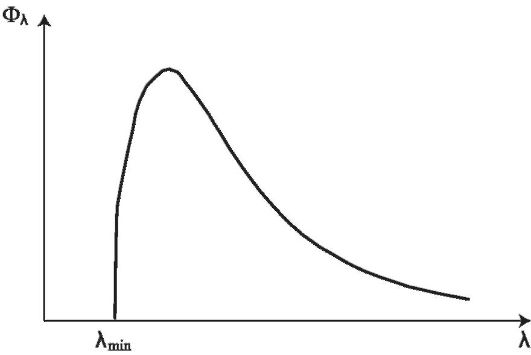Рис. 32.2. Спектр тормозного рентгеновского излучения

Со стороны длинных волн спектр ограничен длиной волны 100 нм, которая является границей рентгеновского излучения. Со стороны коротких волн спектр ограничен длиной волны λ_min. Согласно формуле (32.2) минимальной длине волны соответствует случай Q = 0 (кинетическая энергия электрона полностью переходит в энергию кванта):

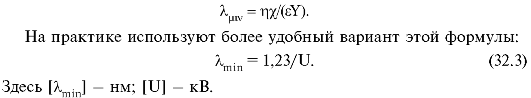Расчеты показывают, что поток (Φ) тормозного рентгеновского излучения прямо пропорционален квадрату напряжения U между

анодом и катодом, силе тока I в трубке и атомному номеру Z вещества анода:

Спектры тормозного рентгеновского излучения при различных напряжениях, различных температурах катода и различных веществах анода показаны на рис. 32.3.

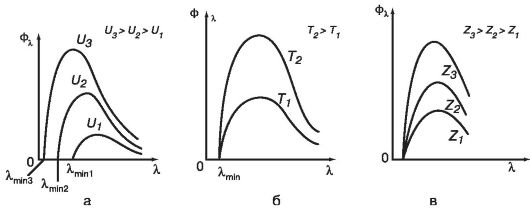Рис. 32.3. Спектр тормозного рентгеновского излучения (Φ_λ):

а - при различном напряжении U в трубке; б - при различной температуре T

катода; в - при различных веществах анода отличающихся параметром Z

При увеличении анодного напряжения значение λ_min смещается в сторону коротких длин волн. Одновременно возрастает и высота спектральной кривой (рис. 32.3, а).

При увеличении температуры катода возрастает эмиссия электронов. Соответственно увеличивается и ток I в трубке. Высота спектральной кривой увеличивается, но спектральный состав излучения не изменяется (рис. 32.3, б).

При изменении материала анода высота спектральной кривой изменяется пропорционально атомному номеру Z (рис. 32.3, в).