Методические указания и контрольные задания для студентов первого курса заочной формы обучения по направлению Психолого-педагогическое образование

2013-2014 уч.г.

1. Задайте множества перечислением элементов

,

.

Решение: делителями числа 6 являются числа 1, 2, 3, 6. Тогда натуральными числами, меньшими 7 и не являющимися делителями 6 являются 4, 5, 7. Значит, .

Рассмотрим уравнение . Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю, т.е. получим три уравнения , , . Решением первого уравнения является , это не целое число, значит, оно не принадлежит . Решением второго уравнения является , это число целое, поэтому принадлежит . У третьего уравнения два корня , , которые также целые и являются элементами . Таким образом, .

2. Для множеств А и В найдите , , , .

а) , ; б) , .

Решение: а) Объединением множеств является множество, состоящее из элементов множеств и , взятых по одному разу. Значит, . Пересечением является множество, составленное из повторяющихся элементов двух множеств, т.е. . Разностью множеств является множество, содержащее элементы множества , не принадлежащие множеству , тогда . Аналогично строим .

б) Данные числовые промежутки , нагляднее изобразить на числовой прямой, при этом, если конец промежутка принадлежит ему, то точка будет закрашенной, а если не принадлежит, то точка – пустая.

Объединением множеств является промежуток от начала первого на числовой прямой множества до конца второго . Пересечением множеств является их общая часть . Разность множеств - это часть множества , которая не принадлежит . При этом важно следить за концами промежутка. В нашем случае элемент 3 не принадлежит , значит, он входит в разность . При нахождении разности отмечаем, что концевая точка 5 принадлежит множеству , значит, этот элемент не входит в разность, т.е. .

3. Представьте множество в виде диаграммы Эйлера.

Решение: представим все этапы построения диаграммы.

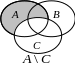
Для того, чтобы построить результирующую диаграмму Эйлера для множеств , возьмем общую часть закрашенных множеств:

4. В одной семье было много детей. Семеро из них любили капусту, шестеро - морковь, пятеро - кабачки. Четверо любили капусту и морковь, трое - капусту и кабачки, двое - морковь и кабачки. А один охотно ел и капусту, и морковь, и кабачки. Сколько детей было в семье?

Решение: решим эту задачу, используя формулу включений и исключений для трех множеств:

Введем следующие обозначения для множеств ={дети, любящие капусту}, ={дети, любящие морковь}, ={дети, любящие кабачки}. Тогда общее количество детей в семье можно представить как . Из условия задачи следует, что , , . Кроме того, , , и . Тогда, подставив найденные значения в формулу включений и исключения, получим:

.

Таким образом, в семье было 10 детей.

5. На доске написаны 3 существительных, 5 прилагательных и 4 глагола. Для составления предложения можно выбрать либо существительное и глагол, либо один глагол, либо все три части речи. Сколькими способами можно составить предложение?

Решение: существительное и глагол можно выбрать способами, один глагол можно выбрать 4-мя способами, три части речи можно выбрать . Тогда по правилу суммы, получим, что общее количество вариантов составить предложение равно .

6. Сколькими способами можно сделать трехцветный флаг с горизонтальными полосами одинаковой ширины разного цвета, если имеется материя шести различных цветов?

Решение: так полос разного цвета необходимо три, а всего имеется 6 различных цветов материи, получаем комбинаторную конструкцию размещения без повторений.

Количество таких размещений вычисляется по формуле . В данном случае , . Тогда .

7. В коробке 4 синих, 3 белых и 2 желтых фишки. Наугад из ящика вынули четыре шара. Какие из следующих событий невозможные, случайные, достоверные: А={вынуты шары одного цвета}; В={все вынутые шары желтые}; С={среди вынутых шаров есть не красные}. Ответ обоснуйте.

Решение: событие А – случайное, так как можно вынуть четыре синих шара, но можно вынуть и шары других цветов, поэтому. данное событие может произойти или не произойти.

Событие В – невозможное, так как всего имеется 2 желтых шара, поэтому среди вынутых шаров обязательно будут и шары других цветов, значит, указанное событие не произойдет никогда.

Событие С – достоверное, так как всего красных шаров три, и даже если их всех достали, то четвертый шар обязате6льнго будет не красного цвета, т.е. это событие выполнится всегда.

8. В ящике содержится 5 белых и 6 черных шаров. Из ящика вынимают два шара. Найти вероятность того, что оба шара будут белыми.

Решение: пусть событие А ={оба вынутых шара – белые}. Данное событие можно представить как комбинацию более простых событий: ={первый шар – белый}, ={второй шар – белый}, тогда .

Воспользуемся теоремой об умножении вероятностей: . Найдем каждый из множителей: , . Подставим их в формулу:

.

9. На предприятии, изготавливающем замки, первый цех производит 25% всех замков, второй цех 35%, третий 40%. Брак по каждому цеху составляет соответственно 5%, 4%, 2%. Найдите вероятность того, что случайно выбранный замок является дефектным.

Решение: обозначим через , , события, состоящие в изготовлении замка соответственно в первом, втором и третьем цехах. Вероятности этих событий равны: , , . Вероятность того, что случайно выбранный замок является дефектным, найдем по формуле полной вероятности: . Найдем условные вероятности: , , .

Тогда .