1.2. Основное уравнение продольной разнотолщинности полосы при прокатке в горизонтальных валках

В соответствии с уравнением Головина-Симса имеем

, (7.1)

где h₁ – толщина полосы, выходящей из валков; S₀ – исходный раствор ненагруженных валков; Р – сила прокатки; M_к – модуль жесткости клети.

Второй член уравнения (7.1) является упругой деформацией клети (валков, станины, нажимных винтов и гаек, подшипников, подушек и пр.).

Сила прокатки зависит от многих переменных, основными из них являются

P = f (h₀, h₁, b, ₀, ₁, _Т, R) , (7.2)

где h₀ и h₁ – толщина полосы до и после прокатки; b – ширина полосы; ₀ и ₁ – заднее и переднее удельные натяжения полосы; _Т – сопротивление деформации стали; R – радиус рабочих валков.)

Функция (7.2) нелинейна. Линеаризацию её производят путем разложения в ряд Тейлора около начальных значений переменных, пренебрегая членами выше первого порядка. Приращения давления металла на валки приближенно округляют как полные дифференциалы

. (7.3)

В качестве функции (7.2) выбирают известные зависимости для расчета силы прокатки.

Продольную разнотолщинность полосы определяют как полный дифференциал уравнения (7.1)

. (7.4)

В процессе прокатки рабочие нагрузки находятся в области линейного участка зависимости упругой деформации клети (см. рис.62). Пренебрегая изменением модуля упругости материала деталей клети в зависимости от колебания температуры и толщины масляной пленки в ПЖТ, второй член уравнения (7.4) не учитывают, и тогда

. (7.5)

При подстановке уравнения (7.3) в уравнение (7.5) получаем основное уравнение продольной разнотолщинности полосы

). (7.6)

По физическому смыслу коэффициенты у дифференциалов представляют собой передаточные коэффициенты, характеризующие влияние независимых переменных параметров процесса прокатки на разнотолщинность полосы.

Выражение в скобках представляет собой изменение силы прокатки за счет непостоянства различных параметров прокатки, кроме выходящей толщины полосы. Поэтому уравнение (7.6) можно записать в виде

.

Углы наклона ₁ и ₂ упруго-пластичной кривой полосы являются модулем жесткости полосы М_п, поэтому в окончательном виде основное уравнение продольной разнотолщинности имеет следующий вид

. (7.7)

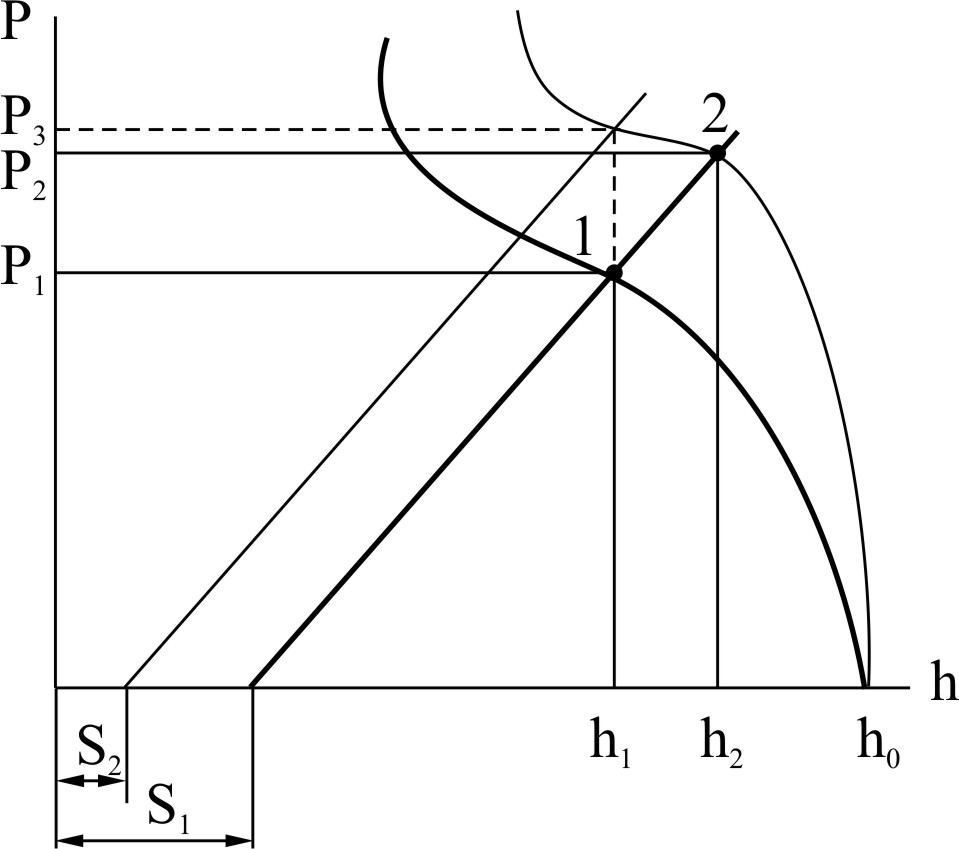
Совместное решение уравнения упругой деформации клети и кривой пластичности приведено на рис.64.

Рис.64. Схема к выводу основного уравнения продольной разнотолщинности полосы

Точка 1 характеризует толщину полосы (h₁) после прокатки. При изменении свойств полосы (например, изменение температуры прокатки) и одной и той же исходной толщине толщина полосы изменится и станет h₂ > h₁. Изменится и сила прокатки Р₂ > Р₁ . Для того, чтобы получить ту же толщину полосы, что была в первом случае, необходимо изменить раствор валков с S₁ на S₂.

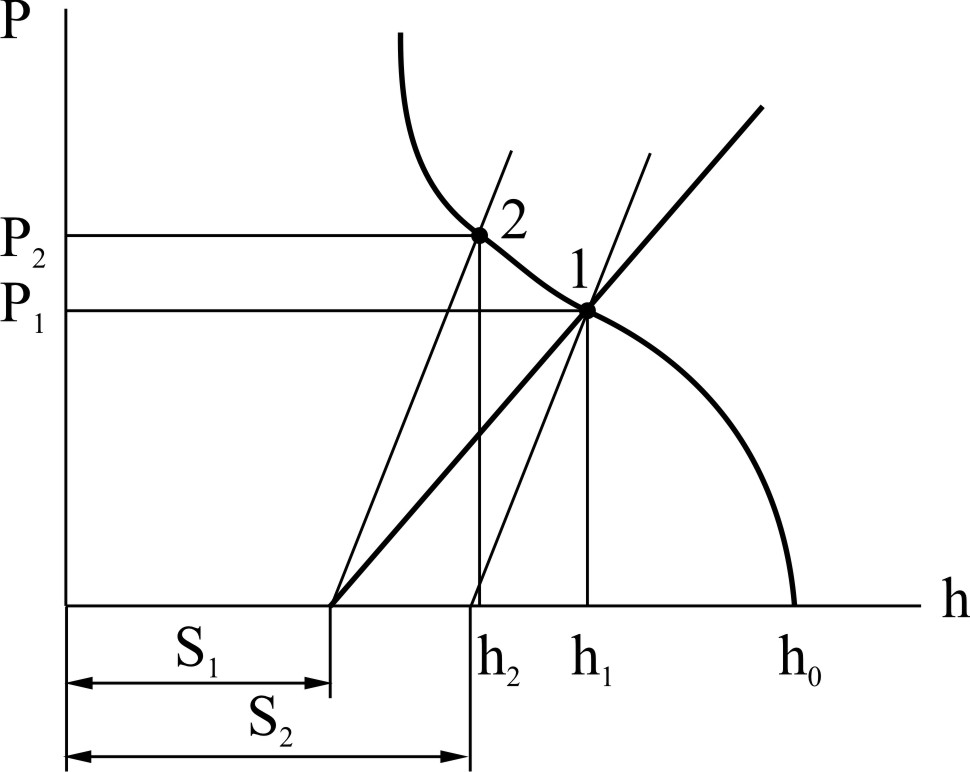
При изменении модуля жесткости клети (например, применении гидрораспора) толщина полосы уменьшится, а сила прокатки увеличится Р₂ > Р₁ (рис.65). Если же необходимо будет прокатывать прежнюю толщину полосы h₁, то придется увеличивать раствор валков до S₂ (уменьшается «пружина» клети).

Рис.65. Схема изменения толщины полосы при изменении Мк

Представленные графические решения позволяют прогнозировать получающуюся толщину полосы, а если необходимо, то и значения величины изменения раствора валков. Можно использовать методику и для анализа колебаний толщины полосы в зависимости от параметров, входящих в уравнение (7.6).

Например, для выявления степени влияния входной толщины на выходную толщину в каждой клети непрерывного стана, в уравнении (7.6) принимаем: S=0; b=0; ₀=0; ₁=0; _Т=0; R=0 и получаем

(при ).

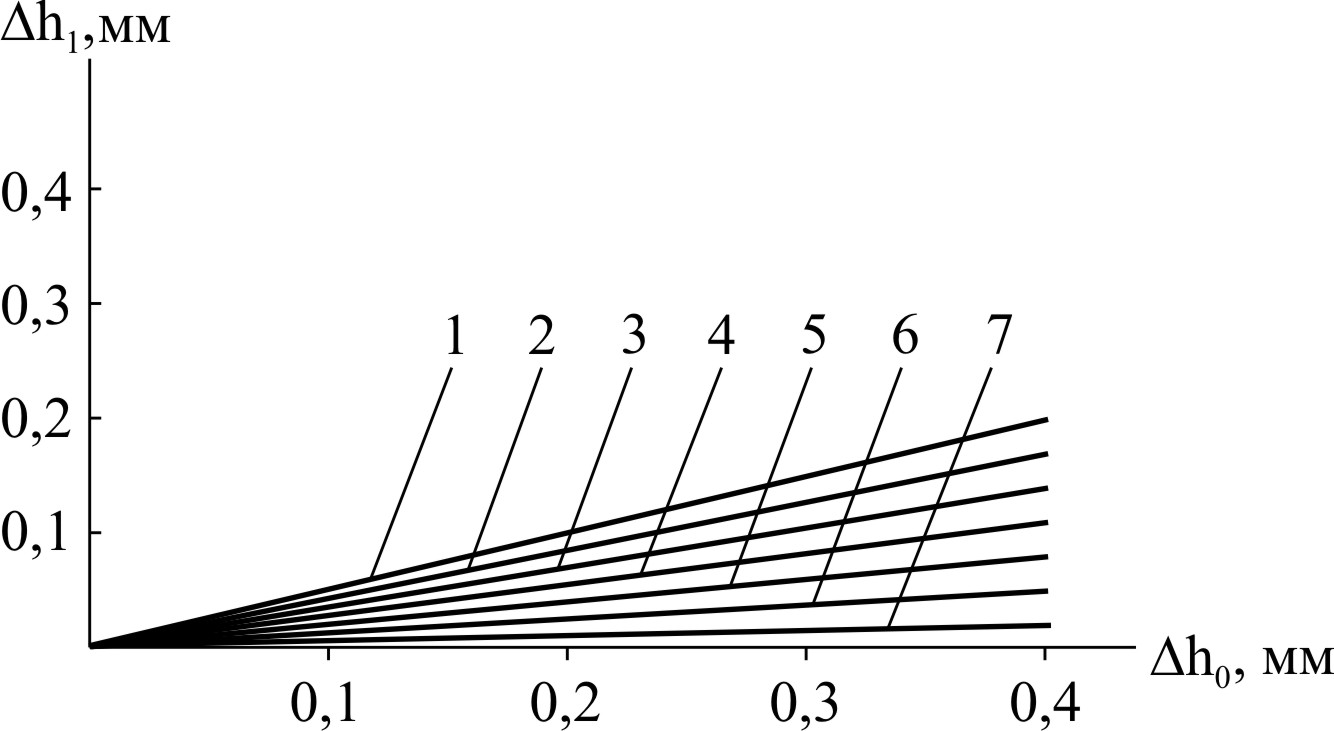
Полученные результаты удобно представить в виде графиков, один из которых показан на рис.66.

Рис.66. Зависимость h1 от h0 при прокатке полосы конечным сечением 21000 мм в каждой из клетей чистовой группы ШСГП (1-7)

Из рисунка видно, что если в первую клеть чистовой группы входит полоса с разнотолщинностью 0,4 мм, то после первой клети её разнотолщинность будет примерно 0,2 мм, в седьмой же клети при h₀ = 0,4 мм имеем h₁ = 0,02 мм.

С применением описанной методики определяют значения технологических передаточных коэффициентов для систем автоматики.