СОДЕРЖАНИЕ

ВВЕДЕНИЕ 2

1. ПОСТАНОВКА ЗАДАЧИ 4

1.1 Качественное описание исследуемой операции 4

1.2 Концептуальная модель операции 5

1.3 Математическая постановка задачи 6

2. АЛГОРИТМИЗАЦИЯ РЕШЕНИЯ ЗАДАЧИ 7

2.1 Анализ методов решения задачи 7

2.2 Выбор и описание метода 8

2.3 Конструирование алгоритма решения задачи 10

2.4 Проектирование сценария диалога 16

2.5 Описание структур данных 19

2.6 Структурная схема алгоритма сценария диалога и описание его программной реализации 21

2.7 Структурная схема функционального алгоритма решения задачи 22

3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ 24

3.1 Ручная реализация алгоритма решения задачи 24

3.2 Машинные эксперименты с разработанными данными 29

3.3 Сравнение результатов ручного и машинного расчетов 32

ЗАКЛЮЧЕНИЕ 33

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 34

ПРИЛОЖЕНИЕ А – ЛИСТИНГ ПРОГРАММЫ 35

Введение

Одной из задач принятия решений является задача оптимального резервирования элементов сложной системы.

Большая группа задач оптимизации связана с определением числа резервных элементов (подсистем) с учетом ограничивающих факторов (затрат). Подобные задачи могут быть двух видов. Задачи оптимального резервирования первого вида состоят в определении требуемого количества резервных элементов, обеспечивающих заданное значение показателя надежности системы при минимальных затратах. Задачи второго вида - определение требуемого количества резервных элементов, обеспечивающих максимум значения показателя надежности системы при величине затрат, не превышающей заданную.

Для решения перечисленных задач используют метод неопределенных множителей Лагранжа, а также методы: градиентный, перебора и динамического программирования.

Целью курсовой работы является количественное исследование, данной в задании ситуации сложной системы.

Для достижения этой цели в работе решаются следующие задачи: на основе содержательного описания исследуемой операции предлагается ее концептуальная модель и дается математическая постановка задачи; для предложенного метода решения разрабатывается его подробный алгоритм и структурная схема; для Intel-совместимой ЭВМ составляется и отлаживается программа и выполняется количественное исследование операции с помощью ручных и машинных расчетов.

1. Постановка задачи

   1. Качественное описание исследуемой операции

На предприятии необходимо выполнить разгрузочно-погрузочные работы на M складах предприятия. Время выполнения работы на каждом складе зависит от количества грузчиков 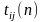- где n количество грузчиков, занятых на j-м складе при i-м варианте распределения грузчиков. На предприятии имеются грузчики в количестве N человек. Требуется сформировать бригады на каждый склад таким образом, чтобы выполнить все работы за минимальное время.

1.2. Числовые данные:

M=5, N =21

Таблица 1.- Время выполнения работы

Количество грузчиков	Склад
	№1	№2	№3	№4	№5
2	10	12	14	8	18
4	6	8	9	5	12
5	5	6	6	3	10
6	3	4	4	2	8
8	2	3	2	1	4

2. Концептуальная модель операции

Задача оптимизации формирования численности бригад сводится к минимаксной задаче оптимального распределения программных модулей между процессорами, которая формулируется следующим образом:

В результате проектирования информационной системы выделено множество программных модулей R={R₁,...,R_i,....,R_m}. Эти модули являются информационно-независимыми друг от друга и могут параллельно выполняться на многопроцессорной вычислительной системе, которая содержит D_o процессоров. Для каждого из программных модулей определены варианты их реализации, которые формально задаются переменной d_{ij ,} определяющей количество процессоров, которые могут использоваться для выполнения R_i-го программного модуля в j-м варианте. Необходимо распределить имеющиеся процессоры по программным модулям, чтобы их выполнение было закончено в кратчайшее время, т.е. следует уменьшить отрезок времени, начинающийся с момента начала выполнения работ и заканчивающийся в момент выполнения последнего модуля.

• Количество грузчиков n, занятых на j-м складе при i-м варианте распределения грузчиков соответствует количеству процессоров d_ij , которые могут использоваться для выполнения программного модуля в j-м варианте;

• Процессор D_i (по условию задачи N) ставится в соответствие складу М_j;

Наличие этих соответствий и позволяет свести на концептуальном уровне решаемую задачу к минимаксной задаче оптимального распределения программных модулей между процессорами и применить для её решения алгоритмы, разработанные для данной задачи.