Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Военно-космическая академия им. А.Ф. Можайского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

l05-08.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

1.06 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

1.3. Количество информации в сообщении. Энтропия

В это параграфе мы сформулируем основное теоретико-информационное понятие – количество информации в сообщении. Мы увидим, что информация определяется только вероятностными свойствами сообщений. Все другие их свойства, например, полезность для тех или иных действий, принадлежность тому или иному автору и др., игнорируются. Это специфика теории информации, о которой иногда забывают, что часто приводит к неправильным выводам.

Пусть { }ансамбль сообщений, }.

Определение 1.3.1. Количеством собственной информации (или собственной информацией) в сообщении называется число , определяемое соотношением

, i=1,2,…,L. (1.3.1)

Основание, по которому берётся логарифм в этом определении, влияет на единицу измерения количества информации. Наиболее часто употребляются логарифмы по основанию 2 и натуральные логарифмы. В первом случае единица измерения количества информации называется “бит”, во втором “нат” (от английских “binary digit” и “natural digit”).

Всюду ниже (если не оговорено противное) будем использовать только двоичные логарифмы и измерять количество информации в битах.

Рассмотрим основные свойства количества информации.

1. Собственная информация неотрицательна. Она равна нулю только в том случае, когда сообщение имеет вероятность 1. Такое сообщение можно рассматрить как неслучайное и известное заранее до проведения опыта. То сообщение имеет большую собственную информацию, которое имеет меньшую вероятность.

2. Расмотрим ансамбль { }.Для каждого сообщения из этого ансамбля, т. е. для каждой пары , собственная информация . Если сообщения и статистически независимы, т. е. , то

= . (1.3.2)

Это свойство называется свойством аддитивности информации.

Количество информации, определяемое соотношением (1.3.1), является действительной функцией на ансамбле { }и, следовательно представляет собой случайную величину со значениями .

Определение 1.3.2. Математическое ожидание случайной величины , определённой на ансамбле { }, называется энтропией этого ансамбля:

. (1.3.3)

Энтропия представляет собой среднее количество собственной информации в сообщениях ансамбля .

Замечание. Согласно определению 1.3.1. собственная информация принимает бесконечные значения для сообщений, вероятности которых равны нулю. Однако энтропия любого дискретного ансамбля конечна, так как выражение вида при z =0 по непрерывности доопределяется как 0.

Основанием для такого доопределения является следующее соотношение:

которое получается в результате применения правила Лопиталя для раскрытия неопределённости типа .

Пример 1.3.1. Пусть -двоичный ансамбль и , вероятности его сообщений. В этом случае энтропия является функцией одной переменной .

. (1.3.4)

Эта функция показана на рисунке 1.3.1. В точках и она не определена и в соответствии с предыдущим значением доопределяется до нуля.

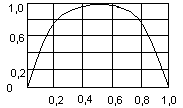
Рис. 1.3.1. Энтропия двоичного ансамбля.

Проведение энтропии как функции от может быть исследовано с помощью вычисления производной от правой части равенства (1.3.4) (см. задачу 1.3.1).

Рассмотрим теперь свойства энтропии.

1. Энтропия всякого дискретного ансамбля неотрицательна:

(1.3.5)

Равенство нулю возможно в том и только в том случае, когда существует некоторое сообщение , для которого ; при этом вероятности остальных сообщений равны нулю.

Неотрицательность следует из того, что собственная информация каждого сообщения дискретного ансамбля неотрицательна. Равенство нулю возможно только тогда, когда каждое слагаемое в (1.3.3) равно нулю, а это равносильно но условию, указанному выше.

2. Пусть L-число сообщений в ансамбле ,тогда

, (1.3.6)

причём равенство имеет место в том случае, когда все сообщения ансамбля имеют одинаковые вероятности.

Это неравенство можно доказать с помощью стандартных методов поиска условного экстремума функции нескольких переменных. Однако имеется простое доказательство, основанное на следующем неравенстве для натурального логарифма:

, (1.3.7)

где равенство имеет место только при (см. рис. 1.3.2). (Неравенство (1.3.7) может быть проверено аналитически, если заметить, что разность ln x- x+1 имеет отрицательную вторую производную и стационарную точку при x=1)

Для доказательства (1.3.6) рассмотрим разность :

Теперь используем неравенство (1.3.7). В результате получим

Отсюда следует неравенство (1.3.6). Поскольку равенство в (1.3.7) имеет место только тогда, когда аргумент логарифма равен единице, то равенство в (1.3.6) имеет место только тогда, когда =1 для всех , т. е. Когда для всех .

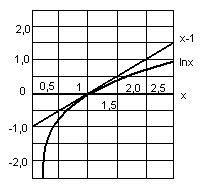
Рис. 1.3.2. К неравенству для логарифма (1.3.7)

Таким образом, энтропия принимает наименьшее значение 0 для ансамбля, в котором сообщения предопределены заранее - одно из них появляется всегда, остальные - никогда. Энтропия принимает наибольшее значение log L, когда все сообщения одинаково вероятны. Эти два свойства часто используют для того, чтобы толковать энтропию как степень или меру неопределённости (степень неопределённости знаний экспериментатора) в эксперименте с получением сообщений ансамбля. Если сообщения заранее предопределены и экспериментатор знает, какой сообщение он получит, то неопределённость и энтропия равны нулю. Если ни одно сообщение не имеет преимуществ по отношению к другим и экспериментатор с одинаковыми шансами может получить любое сообщение, то как неопределённость, так и энтропия максимальны. Такое качественное толкование энтропии полезно, но остановимся на содержательном смысле энтропии как скорости создания информации источником.

3. Пусть и - статистически независимые ансамбли (см. 1.1.4). Тогда для каждой пары сообщений и выполняется равенство (1.3.2). Усредняя левую и правую части (1.3.2) по распределению и учитывая, что есть энтропия ансамбля { }, получим

. (1.3.8)

Это свойство называется свойством аддитивности энтропии.

1.4. Условная информация. Условная энтропия

Пусть{ } – пара совместно заданных дискретных ансамблей { }и { }. Как указывалось выше, на каждом из множеств и могут определены различные условные распределения. Зафиксируем некоторое сообщение , , и рассмотрим условное распределение на . Для каждого сообщения в ансамбле { }определена собственная информация

, (1.4.1)

которая называется условной собственной информацией сообщения при фиксированном сообщении . Как и раньше, можно рассматривать как случайную величину на ансамбле { }; её математическое ожидание

(1.4.2)

называется условной энтропией ансамбля относительно сообщения .

Условную энтропию можно рассматривать как с. в. на ансамбле { }.

Определение 1.4.1. Математическое ожидание случайной величины , определённой на ансамбле { }, называется условной энтропией ансамбля относительно ансамбля :

. (1.4.3)

Замечание. Следует помнить, что условная вероятность , а следовательно, условная собственная информация и условная энтропия , определены только для тех сообщений , вероятности которых отличны от нуля. Поэтому всюду ниже мы будем считать, что указанное условие выполнено и соответствующие вероятности не равны нулю. Если в ансамбле некоторые сообщения имеют нулевые вероятности, то мы будем исключать эти сообщения из рассмотрения, переходя тем самым к ансамблю, все сообщения которого имеют ненулевые вероятности.

Мы ввели условную энтропию , рассматривая в начале условную энтропию при фиксированном сообщении как случайную величину на ансамбле , а затем находя математическое ожидание этой с. в. Можно поступить иначе и рассмотреть условную собственную информацию как действительную функцию, заданную на ансамбле{ , } и, следовательно, как с. в. на этом ансамбле. Тогда энтропия есть математическое ожидание с. в. и может быть непосредственно определена с помощью правой части формулы (1.4.3).

Теперь мы продолжим рассмотрение свойств энтропии и условной энтропии.

1. Условная энтропия не превосходит безусловной энтропии того же ансамбля:

. (1.4.4)

причём равенство имеет место в том и только в том случае, когда ансамбли и статистически независимы.

Доказательство этого неравенства приводится с помощью неравенства для логарифма (1.3.7):

. (1.4.5)

Равенство выполняется в том и только в том случае, когда = для всех , .

1. Математическое ожидание собственной информации пары сообщений

(1.4.6)

по определению представляет собой энтропию ансамбля . Используя соотношение (определение условной вероятности), можно получить, что

. (1.4.7)

Аналогично, используя соотношение , можно получить, что

. (1.4.8)

Эти свойства также называются свойствами аддитивности энтропии. В случае независимых ансамблей соотношения (1.4.7) и (1.4.8) переходят в (1.3.8).

3. Предположим, что задан ансамбль { }и на этом ансамбле определено отображение множества в множества . Это отображение определяет ансамбль { }, для которого . Пусть , - энтропии ансамблей и соответственно. Тогда

(1.4.9)

и знак равенства имеет место в том и только том случае, когда отображение обратимо, т. е. Когда каждому элементу соответствует один и только один элемент .

Для доказательства неравенства (1.4.9) заметим, что совместное распределение вероятностей на произведении множеств и задаётся следующим образом: , где для и для остальных . Другими словами, каждое сообщение ансамбля однозначно определяет сообщение ансамбля (в этом случае говорят, что ансамбль однозначно определяет ансамбль ). Тогда, как легко показать (см. задачу 1.4.1), . Из аддитивности и неотрицательности энтропии получим, что

. (1.4.10)

Таким образом, при произвольных отображениях, задаваемых функцией , при которых ансамбль переходит в некоторый другой ансамбль , энтропия не возрастает. Энтропия не изменяется тогда и только тогда, когда =0, т. е. Когда ансамбль однозначно определяет ансамбль . Другими словами, энтропия сохраняется только при необратимых преобразованиях.

4. Пусть { }- три совместно заданных ансамбля и

(1.4.11)

-условная собственная информация сообщения при фиксированной паре сообщений где

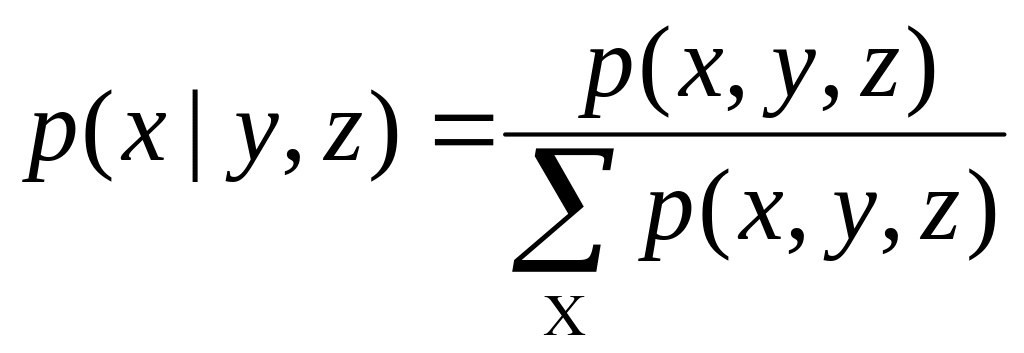. (1.4.12)

Число

(1.4.13)

Называется условной энтропией ансамбля относительно пары ансамблей .

Имеет место, следующее неравенство:

, (1.4.14)

которое доказывается таким же методом, как и неравенство (1.4.4). Равенство в (1.4.14) выполняется в том и только том случае, когда для всех ( ) , т. е. Когда при данном сообщении ансамбли и статистически независимы.

Это неравенство легко обобщается на случай n совместно заданных ансамблей. Рассмотрим ансамбль { }. Тогда для любых s и m, , имеет место следующее неравенство: