3.4. Синтез rc-двухполюсников

Требуется реализовать функцию входного сопротивления , имеющую полюсы , .

Разложение данного выражения на простые дроби по первому методу Фостера имеет вид:

.

Первые два слагаемых разложения отличны от нуля, поскольку существуют полюсы и на бесконечности, и в начале координат. Число слагаемых, стоящих под знаком суммы, равно единице, поскольку существует один полюс, отличный от нуля и бесконечности. Находим коэффициенты:

;

;

.

То есть получили . Согласно этому выражению схема реализации содержит последовательно включенные активное сопротивление Ом, конденсатор емкостью Ф и параллельные друг другу резистор сопротивлением Ом и конденсатор емкостью Ф.

С

Рис. 3.10. Схема реализации RC-двухполюсника по первому методу Фостера

хема такого двухполюсника представлена на рис. 3.10.

По второму методу Фостера реализуется функция входной проводимости, т. е. функция

.

Согласно (2.8) разложение на простые дроби имеет вид:

,

где коэффициенты , и определяются как вычеты функции в соответствующих полюсах:

.

Поскольку степень полинома знаменателя функции больше степени полинома числителя, то полюс на бесконечности отсутствует, и коэффициент . В знаменателе дроби отсутствует множитель, который можно вынести за скобку, т.е. нет полюса в начале координат. Следовательно . Полюсами функции являются два значения и . Следовательно, количество слагаемых, стоящих под знаком суммы, также равно двум. Определяем коэффициенты :

; .

В

Рис. 3.11. Схема реализации RC-двухполюсника вторым методом Фостера

итоге получаем . Такому представлению функции соответствует схема, состоящая из двух параллельных ветвей, в каждой из которых активное сопротивление и конденсатор соединены последовательно так, как это показано на рис. 3.11. Находим значения сопротивлений и емкостей:

Ом; Ом;

Ф; Ф.

Реализуем заданную функцию первым методом Кауэра, располагая слагаемые полиномов числителя и знаменателя в порядке убывания степеней, т. е.

.

Делим числитель на знаменатель:

П

Рис. 3.12. Схема реализации

RC-двухполюсника первым методом Кауэра

ервый шаг деления дает сопротивление , представляющее собой резистор сопротивлением Ом. На втором шаге деления получаем емкостную проводимость, которой соответствует значение емкости Ф. Далее вновь следует активное сопротивление величиной Ом, и на последнем шаге деления имеем емкостную проводимость , которой соответствует значение емкости Ф. Схема двухполюсника показана на рис. 3.12.

Вторым методом Кауэра реализуем заданную функцию входного сопротивления, располагая слагаемые полиномов числителя и знаменателя в порядке возрастания степеней, т. е. представив ее в виде:

.

Делим числитель на знаменатель:

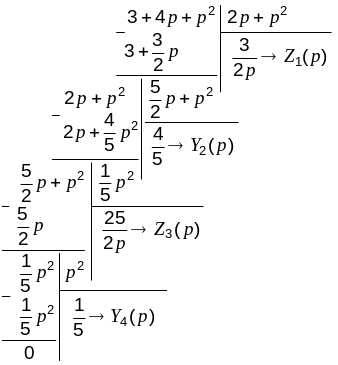
С

Рис. 3.13. Схема реализации RC-двухполюсника вторым методом Кауэра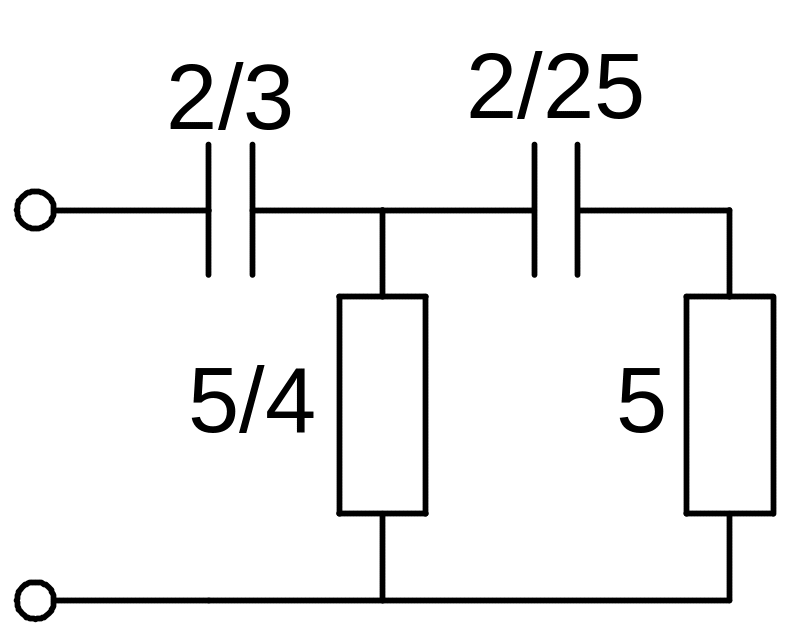

опротивление есть емкостное сопротивление, которому соответствует значение емкости Ф. Проводимость – это активная проводимость, соответствующая резистивному сопротивлению Ом. Далее вновь следует емкостное сопротивление со значением емкости Ф, и на последнем шаге деления получаем активную проводимость , определяющую резистивное сопротивление Ом.

Схема двухполюсника, синтезированная с помощью данного метода, представлена на рис. 3.13.