2.2. Синтез реактивных двухполюсников

Реактивными называются двухполюсники, схемы которых состоят только из элементов L и C. Характерными признаками двухполюсников такого вида являются:

1. нули и полюсы входной функции простые и лежат на мнимой оси взаимно чередуясь. В начале координат плоскости комплексной переменной может располагаться как нуль, так и полюс;

2. в выражении (1.1а) наибольшая (наименьшая) степень полиномов числителя и знаменателя отличаются на единицу. Это означает, что полином четный, а полином – нечетный или наоборот;

3. значения самой функции на мнимой оси (т. е. ) являются чисто мнимыми и возрастают с ростом частоты, т. е.

.

Реализация двухполюсника по первому методу Фостера подразумевает разложение функции входного сопротивления на простые дроби

. (2.1)

В этом разложении: N – число пар комплексно-сопряженных полюсов функции ; , , – постоянные действительные, положительные коэффициенты, определяемые как вычеты функции в полюсах , и соответственно и вычисляемые по формулам:

, ,

.

где – производная полинома знаменателя функции .

Сравнивая каждое из слагаемых с данными табл. 1 нетрудно заметить, что первое из них представляет собой индуктивное сопротивление (стр. 1 табл. 1), индуктивность которого , второе – емкостное сопротивление (стр. 2 по табл. 2) с емкостью , а выражение под знаком суммы – параллельное соединение индуктивности и емкости (стр. 4 по табл. 1).

Очевидно, что схема двухполюсника, реализуемого с помощью разложения (2.1), должна представлять собой последовательное соединение данных сопротивлений (рис. 2.1).

Рис. 2.1. Первая каноническая схема Фостера

Данная схема содержит индуктивность только в том случае, когда степень полинома числителя на единицу превышает степень полинома знаменателя (функция имеет полюс на бесконечности), и емкость , если в полиноме знаменателя переменная может быть вынесена за скобки как множитель.

Реализация двухполюсника по второму методу Фостера подразумевает разложение на простые дроби функции входной проводимости:

, (2.2)

где – число пар комплексно-сопряженных полюсов функции ; , , – постоянные действительные положительные коэффициенты, определяемые как вычеты функции в полюсах , и соответственно и вычисляемые по формулам:

; ;

.

В этих формулах также есть производная полинома знаменателя функции .

Сопоставив каждый член разложения (2.2) с данными табл. 1 можно сделать вывод, что первое слагаемое есть емкостная проводимость (стр. 2 табл. 1) со значением емкости , второе – индуктивная проводимость (стр. 1 табл. 1) со значением индуктивности , а дробное выражение, стоящее под знаком суммы – проводимость ветви с последовательным соединением элементов и (стр. 9 табл. 1).

Схема двухполюсника, соответствующая разложению (2.2), изображена на рис. 2.2.

Рис. 2.2. Вторая каноническая схема Фостера

Синтезируемый двухполюсник содержит емкость только в том случае, когда степень полинома числителя функции на единицу превышает степень полинома знаменателя (функция имеет полюс на бесконечности), и индуктивность , если в знаменателе переменная может быть вынесена за скобки как множитель (функция имеет полюс при ).

Синтез двухполюсников методами Кауэра производится путем представления заданной операторной входной характеристики в виде лестничной дроби с элементами типа или . Если есть функция входного сопротивления, то цепная дробь имеет вид:

(2.3)

При этом если члены полиномов числителя и знаменателя входной функции сопротивления располагаются в порядке убывания степеней переменной , то цепная дробь записывается как

, (2.3а)

которой соответствует первая каноническая схема Кауэра, изображенная на рис. 2.3.

При расположении членов полиномов числителя и знаменателя функции в порядке возрастания степеней переменной , цепная дробь будет иметь вид:

, (2.3б)

которому соответствует вторая каноническая схема Кауэра, изображенная на рис. 2.4.

Рис. 2.3. Первая каноническая схема Кауэра	Рис. 2.4. Вторая каноническая схема Кауэра

Если в качестве входной функции двухполюсника выступает функция входной проводимости , то в общем виде цепная дробь будет выглядеть следующим образом:

. (2.4)

При расположении слагаемых полиномов числителя и знаменателя по убывающим степеням переменной цепная дробь будет иметь вид:

(2.4а)

и соответственно первая каноническая схема Кауэра для этого случая изображена на рис. 2.5.

Если слагаемые полиномов числителя и знаменателя расположены по возрастающим степеням переменной , то лестничная дробь есть дробь вида:

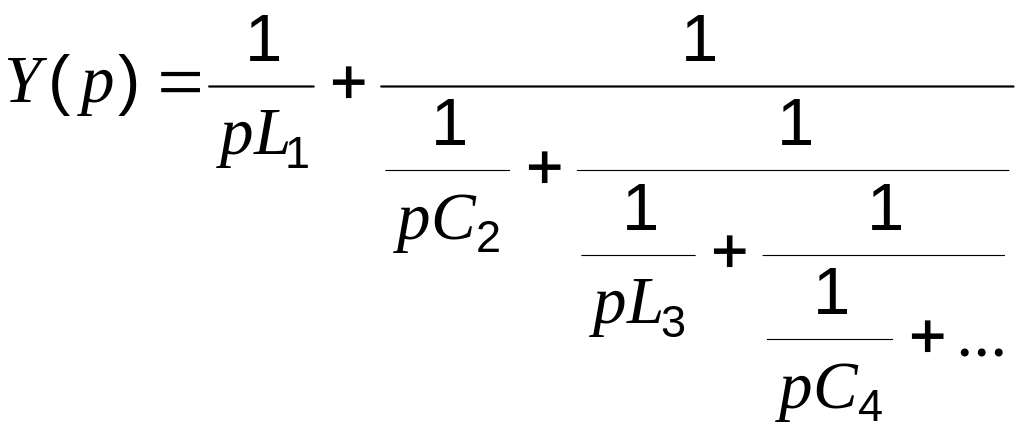. (2.4б)

На рис. 2.6 изображена соответствующая ей вторая каноническая схема Кауэра.

Рис. 2.5. Первая каноническая схема Кауэра	Рис. 2.6. Вторая каноническая схема Кауэра

Общим для всех случаев реализации реактивных двухполюсников методами Кауэра является то, что во всех схемах элементы с индексами 1 и могут отсутствовать. Первая каноническая схема Кауэра содержит элемент с индексом 1 (рис. 2.3 и 2.5) только в том случае, когда операторные входные функции (сопротивление или проводимость) имеют полюс на бесконечности. Вторая каноническая схема Кауэра содержит элемент с индексом 1 (рис. 2.4 и 2.6) только тогда, когда операторные входные функции (сопротивление или проводимость) имеют полюс в нуле. Наличие или отсутствие элементов с индексом зависит лишь от числа шагов деления полиномов числителя и знаменателя до момента получения нулевого остатка. При выполнении деления необходимо следить, чтобы численные коэффициенты при переменной оставались положительными, а степени самой переменной были равны 1 или –1. Если же в процессе деления какой-либо из коэффициентов окажется отрицательным, то на данном шаге необходимо изменить расположение слагаемых полиномов, т. е. перейти либо от убывания степеней переменной к их возрастанию, либо наоборот.