2. Расчет и построение частотных характеристик

Для наглядного представления о частотных характеристиках четырёхполюсника используют их графики, построенные по выражениям (7) и (8), общей вид которых соответствует выражению (9). При подставке в эти выражения численных значений циклической частоты   получаются комплексные числа

.

На графиках изображают отдельно частотную зависимость модуля   и аргумента   этого комплексного числа.

Поскольку модуль дроби (9) равен отношению модулей числителя и знаменателя то

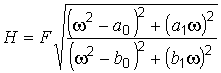                                                ,                                          (11)

где  ,   – соответственно действительные части комплексных числителя и знаменателя дроби (9);  ,   – соответственно мнимые части числителя и знаменателя дроби (9).

Аргумент частотной характеристики, записанной в виде дроби, равен разности аргументов числителя и знаменателя

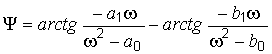                                          .                                      (12)

При вычислениях по выражению (12) без применения специальных калькуляторов и программ необходимо помнить, что при отрицательных действительных частях   и   соответствующих комплексных чисел эти комплексные числа расположены в левой части комплексной плоскости и аргумент такого числа больше   или меньше  . В этом случае при   к вычисленному значению 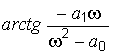  надо прибавить  ,а при   от  надо отнять  . То же относится и к  .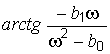

Зависимость модуля комплексного коэффициента передачи по напряжению от частоты называется амплитудно-частотной характеристикой (АЧХ) и показывает зависимость от частоты отношения амплитуд напряжений на выходе и входе четырёхполюсника. Применительно к выражению (7) АЧХ в соответствии с (11)

.

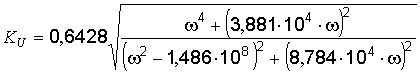Зависимость аргумента комплексного коэффициента передачи по напряжению от частоты называется фазочастотной характеристикой (ФЧХ). Она показывает сдвиг по фазе между выходным и входным напряжениями четырёхполюсника в зависимости от частоты. Для рассматриваемого четырёхполюсника по выражениям (7) и (12) ФЧХ

.

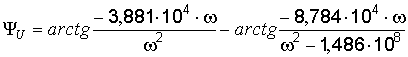астотная зависимость модуля входного сопротивления четырёхполюсника показывает отношение амплитуд входного напряжения и входного тока, т.е. полное сопротивление четырёхполюсника входному току на различных частотах. Для четырёхполюсника рис. 1 в соответствии с (8) и (11)

.

Частотная зависимость аргумента входного сопротивления четырёхполюсника показывает сдвиг по фазе между входным напряжением и входным током четырёхполюсника на разных частотах. Для рассматриваемого четырёхполюсника с учётом (8) и (12)

.

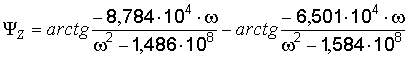Диапазон и количество частот для расчёта и построения графиков частотных характеристик студент выбирает самостоятельно исходя из того, что графики должны полно и наглядно отображать все особенности рассматриваемых характеристик. Для полноты отображения свойств частотных характеристик необходимо нижнюю   и верхнюю   границы частотного диапазона выбирать так, чтобы на этих частотах характеристика приближалась к вычисленным ранее значениям Н(0) и Н( ) и отличалась от них не более, чем на 5–10 % (рис. 4 ).

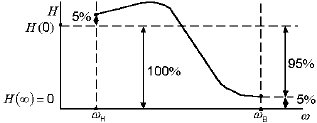
Рис. 4. Выбор границ частотного диапазона

Частотный диапазон ФЧХ можно выбрать таким же, что и у соответствующей АЧХ. Количество расчётных точек графика и их расположение на частотной оси выбирается из условия отражения графиком всех характерных особенностей частотной характеристики (экстремумы, точки перегиба).

Расчёт численных значений частотных характеристик рассматриваемого четырёхполюсника сведены в табл. 1.

Таблица 1

Частотные характеристики четырёхполюсника

, рад/с		, град	, Ом	, град
100	0.017	86.7	526.0	1.0
200	0.033	83.5	527.4	2.0
400	0.065	77.2	532.8	3.9
700	0.109	68.4	546.6	6.4
1000	0.145	60.7	564.9	8.3

2000	0.22	42.4	631.4	10.4
4000	0.267	26.5	709.5	8.0
7000	0.285	19.4	745.4	4.3
10000	0.293	17.6	754.9	1.9
13642	0.301	17.5	756.8	0
20000	0.316	19.1	751.6	-2.3
40000	0.377	23.2	716.1	-6.5
70000	0.463	23.3	662.2	-8.4
100000	0.522	20.5	626.6	-8.2
200000	0.601	12.8	581.9	-5.7
400000	0.631	6.8	565.9	-3.1
700000	0.639	3.9	561.9	-1.8
1000000	0.641	2.7	560.9	-1.3

Диапазон частот при построении графиков может быть достаточно большим, в таких случаях для оси частот применяют логарифмический масштаб. Для градуирования оси абсцисс при этом от начала координат откладывают расстояние в сантиметрах (или миллиметрах), равное  , а обозначают эту точку численным значением  . Например,   рад/с,   см. Шкалы на осях для большей наглядности графиков могут начинаться не от нулевого значения.

Графики частотных характеристик, построенные по данным табл. 1, приведены на рис. 5, рис. 6, рис. 7 и рис.8.

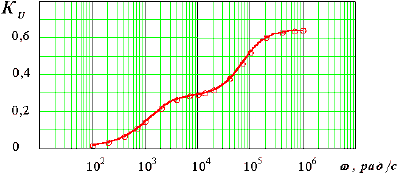
Рис. 5. АЧХ

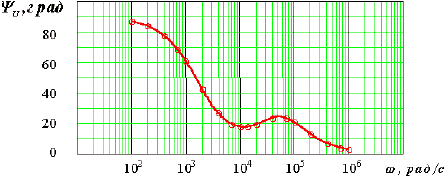
Рис. 6. ФЧХ

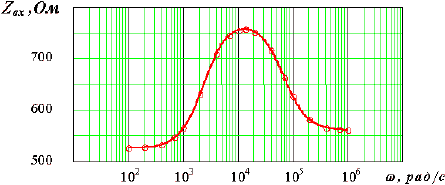
Рис. 7. Частотная характеристика модуля входного сопротивления

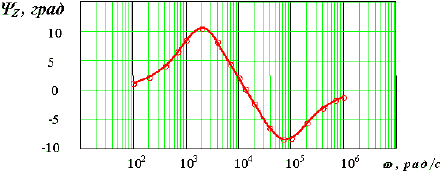
Рис. 8. Частотная характеристика аргумента входного сопротивления

Дополнительный качественный анализ частотных характеристик часто можно провести по схеме четырёхполюсника (рис. 1).

График АХЧ (рис. 5) представляет собой возрастающую функцию. Это связано с тем, что в схеме четырёхполюсника ёмкость   включена вдоль пути передачи сигнала со входа на выход. Поскольку с ростом частоты проводимость ёмкости увеличивается, то большая часть входного сигнала поступает в нагрузку  . Кроме того, в схеме четырёхполюсника индуктивность   включена поперёк направления передачи сигнала. Так как с ростом частоты сопротивление индуктивности возрастает, то меньшая доля сигнала замыкается по ней, а большая поступает в нагрузку. Таким образом, на вид АХЧ влияет не только само наличие элементов с частотно-зависимыми сопротивлениями, но и способ их включения по отношению к направлению передачи сигнала.

Показательными являются так же графики частотной характеристики входного сопротивления четырёхполюсника (рис. 7, рис. 8). На частоте   (см. табл. 1) характеристика аргумента входного сопротивления (рис. 8) пересекает ось абсцисс. Поскольку четырёхполюсник вместе с сопротивлением нагрузки   (рис. 1) можно рассматривать относительно генераторных зажимов   как пассивный двухполюсник, то очевидно, что на этой частоте в нём наступает резонанс ( , т.е. напряжение и ток на входе совпадают по фазе). В данном примере это резонанс токов, поскольку модуль входного сопротивления в окрестности резонансной частоты   имеет явно выраженный максимум (рис. 7).

Подобный анализ частотных характеристик, там где его можно провести, позволяет глубже понять электрические процессы, которые происходят в цепи при передачи по ней сигналов, занимающих тот или иной частотный диапазон.

ПРИЛОЖЕНИЕ

ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ

Линейная пассивная четырёхполюсная цепь подключена к генератору сигналов со стороны зажимов 1, 1', а со стороны зажимов 2, 2' нагружена на приемник сигналов с сопротивлением   (рис. П1).

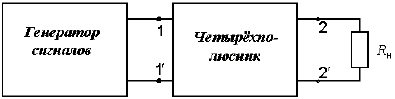
Рис. П1. Четырехполюсник с нагрузкой

Схема четырёхполюсника выбирается по последней цифре варианта из рис. П2, а остальные параметры цепи – из табл. П1, табл. П2 и табл. П3. В выбранной схеме четырёхполюсника необходимо элемент с номером “m” заменить ёмкостью, а элемент с номером “n” – индуктивностью.

Для заданной электрической цепи необходимо:

1.Определить частотную передаточную характеристику по напряжению и частотную характеристику входного сопротивления пассивного четырёхполюсника с нагрузкой  . Сделать проверку при   и  .

2. Рассчитать и построить графики амплитудно-частотной характеристики (АЧХ) и фазочастотной характеристики (ФЧХ), а так же частотные характеристики модуля и аргумента входного сопротивления.

                                          1.                                          2.

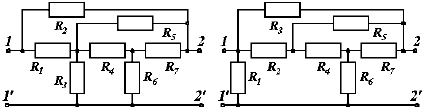
                                           3.                                          4.

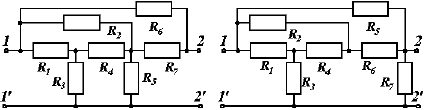
                                          5.                                            6.

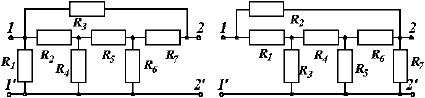
                                 7.                                            8.

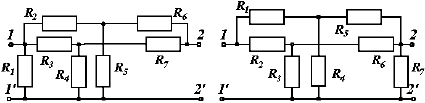
                                  9.                                           0.

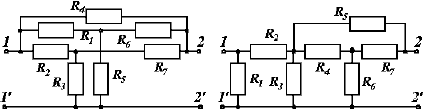
Рис. П2. Схемы четырёхполюсников

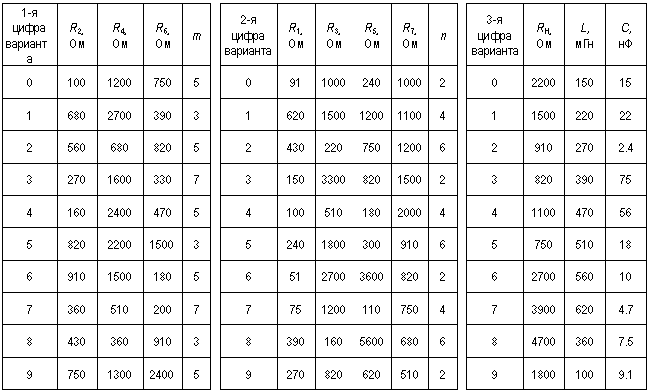
                        Таблица П1                       Таблица П2             Таблица П3

Исходные данные