31. Дайте визначення функції розподілу системи двох випадкових величин і покажіть їх властивості.

Функцією розподілу системи двох випадкових величин наз. Функцією двох аргументів F(x,y) , що дорівнює ймовірності сумісного виконання двох нерівностей Х˂х і Y˂y

Тобто F(x,y) = P(Х ˂х і Y˂y)

Властивості:

1. Якщо один з аргументів наближу до + неск, ф-ція розподілу системи наближу до ф-ції розподілу вип. величини другого аргументу

2. При наближу обох аргументів до + неск ф-ція розподілу F(x,y) наближ до одиниці

3. При наближу одного чи обох аргументів до – нес ф-ція розподілу наближу до 0

4. Ф-ція розподілу F(x,y) є зростаючою ф-цією з кожного аргументу

5. Ймовірність попадання вип. точки (x,y) в будь-який прямокутник зі сторонами, II координатним осям, обчислюэться за формулою

32. Які числові характеристики двомірної випадкової величини?

Числові характеристики є центральний та початковий моменти

Початковим моментом α_sq порядку s, q системи(Х,У) наз мате мат сподівання від добуткаХ^S на Y^q

α_sq = М[Х^S Y^q]

тральним моментом µ _sq порядку s, q системи(Х,У) наз мате мат сподівання добутку центрованих величин(Х – М_х) і (У-М_у) відповідно в s-ому і q-ому степенях

µ _sq = М[(Х – М_х)^S (У-М_у)^q]

33. Що наз кореляційним моментом та коефіцієнтом кореляції?

кореляційний момент К_ху – змішаний центральний момент першого порядкуµ₁₁

µ₁₁ = К_ху = М[(Х – М_х) (У-М_у)]

Коефіцієнт кореляції – коефіцієнт зв`язку К<sub>ху</sub> для оцінки сили зв`язку між вип. величинами системи(Х,У) , змінюється в межах від -1 до + 1

r_xy = К_ху/ õ_x õ_y

34. Приведіть формули кореляційного моменту та коефіцієнта кореляції для сист 2 дискретних вип. величин

кореляційний момент К_{ху =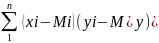} Р_xiyi

Коефіцієнт кореляції r_xy = К_ху/ õ_x õ_y

35. Що називають кореляційною матрицею системи n – випадкових величин?

кореляційною матрицею системи n – випадкових величин наз узагальнене поняття дисперсії D_x для випадкового вектораХ . Визначається за формулою

К_ху = М[(Х – М_х) (У-М_у)^т]

36.Яка матриця наз нормованою кореляційною матрицею?

нормованою кореляційною матрицею К_х наз матрицю, елементами якої є коефіцієнти кореляції

r_ij

1 r12 r1n

r12 1.. r2n

К_{х =} … ….. …..

rn1 rn2 rnn

37.Які задачі вирішує теорія похибок вимірів?

Задачі, які викликають появи похибок,неточне відображення процесів за допомогою мат.,фізичні та технічні. Наприклад, при вимірюванні ліній або кутів, та ін.

З8. Які складові комплексу умов?

об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище), а також точність пристрою,якістю візирних цілей та ін.

39.Назвіть види вимірювань.

- прямі

- безпосередні

- посередні

- непрямі

- рівноточні

- нерівноточні

40.Яка роль надлишкових вимірів?

Різниця між кількістю виконаних вимірів і кількістю необхідних вимірів r = n-k

Важливу роль , метою є отримання якісних характеристик. МОГВ дає можливість отримати як кількісні, так і якісні характеристики(вимір площу, массу вологість, температуру і т.д)

41.Назвіть види похибок вимірів

- випадкові(постійно змін КУ)

- ійовірні

- систематичні та(рулетка) поділ на змінні і постійні

- грубі (промахи)в процесі обчислень

42.Яка природа виникнення випадкових похибок?

Коли змінюється КУ, наприклад,температура або тиск.тому потрібно виконувати багато к-ть досліджень

43.Які виміри є рівноточними?

Коли вони виконані при практично не змінному КУ об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище

44. Які виміри є нерівноточними?

Коли змінюється КУ об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище

45. Що характеризує проста арифметична середина?

Показує, що при неск к-ті вимірів і відсутності систематичних похибок середнє наближ до істинного значення(сер арифм – є більш точним)Вип величини повинні мати однакові математ сподівання(М_хі = М_{х = а)j}, дисперсії не повинні перевищувати наперед відомого додатнього числаD_xi ˂C та мають бути попарнор незалежними i=‡j

При необмеженому збільшенні числа незал. Випробувань сер арифм спостережених значень вип величини, що має кінцеву дисперсію, збігається за ймовірнісю до її матем сподівання

46.Що характеризує СКП m?

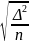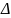Міра точнорсті (емпіричний стандарт)m = де _і = хі – Х

47.Що характеризує СКП µ?

Для виміру, вага якого р = 1, вона буде = скп одиниці ваги µ

µ =

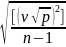
48.Які числові характеристики рівноточних вимірів Ви знаєте?

1 проста арифметична середина Х = [x]/n

2 обчислення різниці Ɛ_i = xi – x0

3 при істинному значенні Х обч величину систематичної похибки λ : λ = Х(з палочкою)-Х

4 Скп окремого виміру або сер арифм

m=

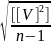
49.Що таке вага виміру і як її визначити?

Вага виміру – це величина рі = С/m, де С – пост. Коефіцієнт ваги ,близький до 1,вказує наскільки точність одного виміру більш або менш точний відносно іншого в ряду вимірів

50.Що характеризує загальне сер арифм?

Характеризує, що при неск к-ті вимірів і відсутн систематичних похибок просте сер арифм наближу до істинного значення .Це одначає, що сер арифм Х (з черточкой) буде найбільш точним, або ймовірним значенням виміряної величини

=[xp]/[p]

51.Що характеризує СКП одиниці ваги?

m_µ= µ/

нерівноточні виміри характеризують дисперсіями m_i ²або мірою відносної точності р_і

характеризує ряд для виміру якого вага р = 1

скп од ваги µ =

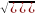
52. Як визначити, що виміри рівно точні?

Якщо вони виконані при практично не змінному КУ об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище

53. Приведіть формулу сер арифм

L (с черточкой) = L₀ + [Ɛ]/n

Або Х (с чертой)= [x]/n, де [x]- сума вимірів

54. Як обчислити систематичну похибку

Систематична похибка обчислюється за ф-лою

λ= [p_dd]/ [p_d], де p_d – вага подвійної різниці d_i

якщо не викон нерівність [/p_dd/] ≤ 0,25[/p_dd/], то необх враховувати дію систематичних похибок і обчислити різниці

d_i ’ = d_i - λ

при відомому істинному значенні Х обчислюють величину систематичної похибки λ

λ = Х (с черточкой) - Х

55. Як обчислити істинні та ймовірні похибки

Істинні похибки включають в себе як випадкові ϭ_і, так і систематичніλ_і, то при n повторних вимірах отримаємо _і = ϭ_і, + λ_і або _і = х_і – Х_і

Ймовірні похибки V_i обчислюються за формулами [pV²] = [pƐ²] - [pƐ²]/ [p]

(ті похибки, які не залежать від природи виникнення)

56. Приведіть формулу Гауса і Бесселя

Ф-ла Бесселя m= 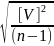V – ймов похибки

Гауса 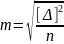, де m – cкп, – похибки

Постулат Гауса :Найбільш імовірне значення шуканої величини є сер арифм із результ повторних вимірювань

57.За яких умов застосовують формулу Гауса, а за якими Бесселя

Гауса , якщо Найбільш імовірне значення шуканої величини є сер арифм із результ повторних вимірювань

Бесселя коли шукана вип. величини Х оцінки дисперсіі буде дещо зміщена

Якщо 1 параметр – проста арифм середина, а 2 – статистична дисперсія

58.Як визначити скп сер арифм?

M = m/ , де m – скп ,n – к-ть вимірів

M_i = µ/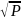 _di

59. Приведіть порядок обробки рівно точних вимірів

1. обчисл арифм середину за ф-лою

Х (с черточкой) = [x]/n

2. при відомому істинному значенні Х обчислюють величину систематичної похибки λ

λ = Х (с черточкой) - Х

3. абсолютні похибки вимірів при заданому істинному значенні Х

Δ_і = х_і - Х(і от 1 до n)

4. величини [pΔ²] та [pV²]

5. Скп окремого виміру , де m – cкп, – похибки

6. СКП сер арифм M = m/ ,

7. скп скп

m_m = m/

8.скп скп арифм середнього

m_M = m/

9. визначають довірчі інтервали для : можливого знач істинної величини, можливих значень результатів вимірів, дисперсії та стандарти сер арифм, стандарт окремих вимірів