1.Що вивчає теорія Ймомірностей?Загальні закономірності випадкових явищ незалежно від їх природи виникнення і пропонує методи кількісної оцінки впливу випадкових факторів на різні явища

2. Дайте визначення подій. Наведіть приклади.Події – це явища,які виникають при реалізації цього КУ(об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище)в результаті проведення випробування.Приклад події – поява помилки виміру вимірювання ліній або кутів, випадання двох гербів при трикратному підкиданні монети та ін.

3.Які події називають випадковими?(ті, які при неодноразовому протікання досліду щоразу протікають інакше)Випадкові події поділяються на елементарні: прості випадкові події (які повністю описуються подією однією)та складні вип. Події(склад. З 2 або більше простих подій)Наприклад, правильний або помилковий результат одного виміру лінії – проста подія, а результат при двох або більше вимірах буде складною подією

4. Що таке комплекс умов?Сукупність умов, при яких проводиться випробування: (об`єкт, суб`єкт, прилад, метод вимірювання, зовн. Середовище), а також точність пристрою,якістю візирних цілей та ін.

5.Як ви розумієте повну группу подій? Наведіть прикладиCукупність різних подій .Наприклад,У результаті підкидання кубика – такі події(А – випало парне число,В – випало число не більше від 3,С – випало число більше ніж 2) – подіїА,В.С – складають повну группу подій

6. Що називають частотою події?частотою події А Наз.відношення числа появи подіїA до числа всіх дослідівQ (Q=k/n). K – число сприятливих подій подіїА, n - число всіх подій

7.Приведіть класичне визначення ймовірностей подій. В яких межах змінюється ймовірність події?Класичне визначення ймовірності - відношення числа сприятливих випадків даної події до загального числа різнозначних випадків.визнач. за формулою:P(A)=M/N, де M – число сприятливих випадків, N - число всіх випадків. Змін. В межах від 0 до 1(0 – неможлива, 1 – достовірна)

8.Що таке принцип практичної впевненості?Практично вірогідною( впевненою) подією наз.подію, величина ймовірності якої досить близька до одиниці .Якщо ймовірність події близька до одиниці чи до нуля, то це дає можлив. Передбачити очікуваний результат.

9.При яких умовах виникає додавання і добуток складних Подій?Додавання виникає за умови такої події, коли: ми маємо справу з складними подіями, які є результатом взаємодії елемент.подій; при випробуваннях виникає хоча б одна з цих подійS=A+B+C+D+…+N)(ймовірність появи однієї з декількох несумісних подій = сумі ймов. Цих подій =1.Сума ймов. Двох протилежн. Подій = 1)Добуток події виникає за умови, якщо подія склад. З N простих подій , то виникає становище, коли вони сумісно з”являються S=A*B*C*…*N

10.Сформулюйте теорему додавання ймовірностейЯкщо події А1, А2, А3, … Аn утворюють повну группу несумісних подій, то сума Їх імовірностей = 1

11.Які події наз. Залежними і незалежними?Подія А наз.незалежною по відношенню до події В, якщо ймовірність події А не залежить від того, виникла подія В чи ні.В противному випадку подію А наз. Залежною від події В.

12. Що таке умовна і безумовна ймовірність?Умовною ймовірністю наз. Імовірність, обчислену в передбаченні того, що одна чи декілька подій уже виникли.

Умова залежності подіїА від подіїВ :Р(А/B)= P(A) , а незалежності (не дорівнює)

Ймлвірність незалежних подій наз.безумовною ймовірністю.

13.Сформулюйте теорему множення ймовірностей

Ймовірність множення двох чи декількох подій = множенню ймовірності однієї з них на умові ймовірності решти подій, розрахованих у передбаченні , що всі попередні події мали місце.

Р(А1,А2, …Аn)= Р1(А1)*Р(А2/А1)….Р(Аn/А1А2…Аn-1)

2 висновки:1 – якщо подія А не залежить від подіїВ, то і подія В не залежить від подіїА,2 – Ймовірність незалежних подій в сукупності подій дорівнює множенню ймовірностей цих подій

14.Сформулюйте теорему додавання ймовірностей для сумісних подій

Ймовірність появи хоча б однієї із двох сумісних подій = сумі ймовірностей цих подій без ймовірності їх сумісного виникнення

Р(А + В) = Р(А) + Р(В) - Р(АВ)

15.В яких задачах виникає необхідність застосування формул повної ймовірності та ймовірності гіпотез необхідність застосування формул повної ймовірності виникає тоді, коли ймовірність події А, що може виникнути разом з однією із гіпотез H1,H2,…Hn = сумі парних добутків ймовірностей кожної із цих гіпотез на відповідні їм умовні ймовірності появи А

Р(А)= сумі від і до n Р(Hі) Р(А/ Hі)

А Ймовірність гіпотез застосув. Тоді, коли є певна група несумісних подій H1,H2,…Hn , та відомі їх ймовірностіР(H1), Р(H2),… Р(Hn).тоді після дослідів з`являється подія А, умовні ймовірності якої = Р(А/ H1), Р(А/ H2),… Р(А/ Hn).

Р(Hі)/A) визнач. За теоремоютгіпотез.

Ймовірність гіпотези після випробувань = добутку ймовірності гіпотезі до випробувань на відповідному їй умовну ймовірність події, що з`явилась при проведенні досліду, поділеному на повну ймовірність цієї події

Р(Hі)/A) = (Р(Hі)* Р(А/(Hі) )/суму від 1 до n Р(Hі)/* Р(А/(Hі)

16. Приведіть формули появи k-ї події при n незалежних випробувань

Pn(k) = 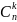* *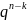 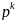, де Pn(k) – ймовірність появи події k разів при n випробуваннях

- число сполучень

Р - ймовірність появи події А в одному випробуванні

q – рівень значності події А в одному випробуванні

17. Як визначити найбільш імовірне число появи подій при повторних випробуваннях?

Якщо однакові ймовірності появи подій, то при повторних випробуваннях існує найбільш імовірне число появи події

Найбільш імовірним числом k появи події А в n незалежних випробуваннях буде число, для якого ймовірність Pn(k) перевищує чи, не менше ймовірності із решти можливих наслідків випробувань.

18. Що наз. Випадковою величиною?

Вип. Величиною наз. Таку величину, яка в результаті досліду може набути б-якого довільного значення до того заздалегідь невідомо якого саме

19.Що наз. З-ном розподілу вип.величини?

З-ном розподілу вип. величини наз. Всяке співвідношення, що встановлює зв`язок між можливими значеннями вип. Величини і відповідними ймовірностями.

З-н розподілу дискретної вип.. величини задають:

Аналітично, чисельно у вигляді таблиці та графічно

20.Дайте визначення ф-ції розподілу та назвіть її властивості.

Ф-цією розподілу (інтегральний з-н розподілу) вип. Величини Х називається задання ймовірності події виконання нерівності Х˂х, де х – деяка поточна змінна. ЇЇ визначають за ф-мулою: F(x) = P( Х˂х)

Властивості:додавання ймовірностей розповсюдж. На всі можливі знач. Вип. Ведичини, які менше х,ф-ція F(x) попаде зліва від точки х

21.Приведіть формулу та властивості щільності розподілу неперервної випадкової величини

Функцією щільності розподілу вип. Величини в т.х є граничне відношення ймовірності попадання її на елементарну ділянку від х до х+ Δх до довжини цієї ділянкиΔх, колиΔх наближ. до 0.

вказує, як часто з`являється вип. Величина Х навколо точки х при повторенні дослідів.

Графік має вигляд кривої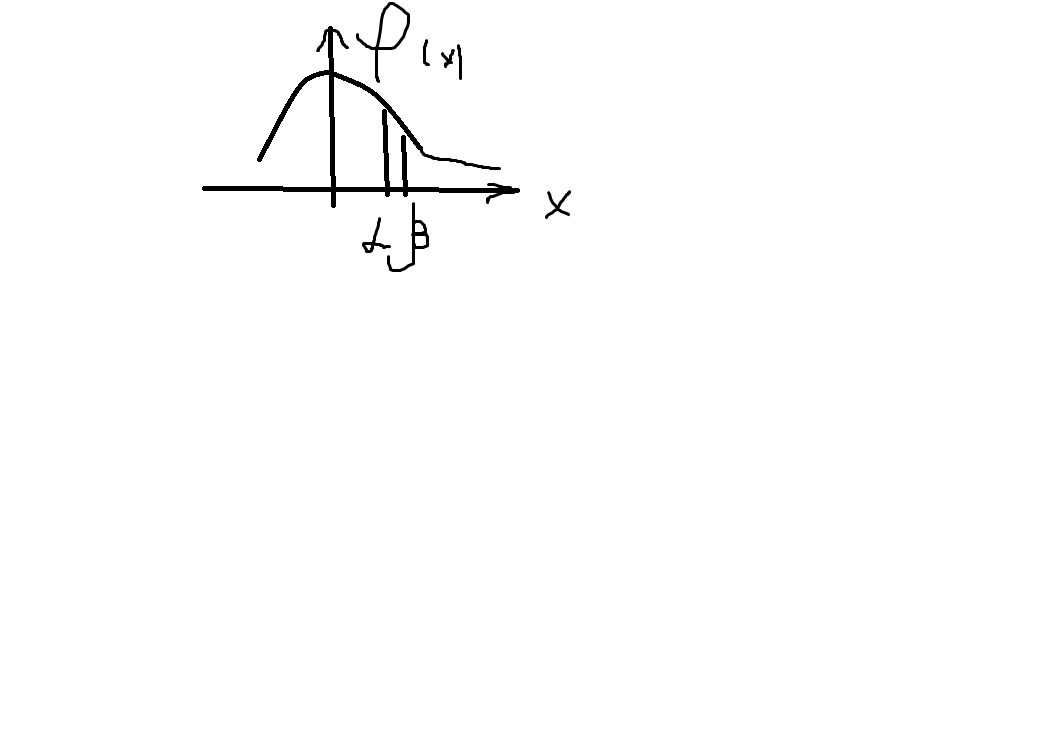

Вл-ті:1.щільність розподілу невід`ємна γ(х)˃либо = 0

2.Ф-ція розподілу вип. Величини = інтегралу від ф-ції щільності в інтервалі віх – неск. До х

3. ймовірність попадання неперервної вип. Величини Х на відрізку(α,β) = інтегралу від ф-ції щільності розподілу, взятому за кінцевими знач. Цього відрізка(ймов = площі трапеції)

4. інтеграл від – неск. До + неск. = 1