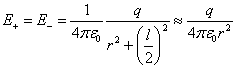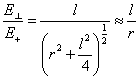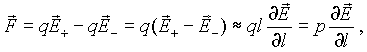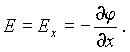Энергия заряженного конденсатора
Если на обкладках конденсатора электроемкостью С находятся электрические заряды +q и -q, то согласно формуле (20.1) напряжение между обкладками конденсатора равно
![]()
В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0.
Среднее значение напряжения в процессе разрядки равно
![]()
Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:
![]()
Следовательно, потенциальная энергия Wp конденсатора электроемкостью С, заряженного до напряжения U, равна
![]()
Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность Е поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.
Вопрос 15.
Электрическим
диполем называется
система двух одинаковых по величине,
но разноименных точечных зарядов,
расстояние между которыми l значительно
меньше расстояния до тех точек, в которых
определяется поле системы (![]() ) (рис.
1.6).
) (рис.
1.6).
Здесь ![]() называют плечо
диполя –
вектор, направленный от отрицательного
заряда к положительному и численно
равный расстоянию между зарядами.
называют плечо
диполя –
вектор, направленный от отрицательного
заряда к положительному и численно
равный расстоянию между зарядами.
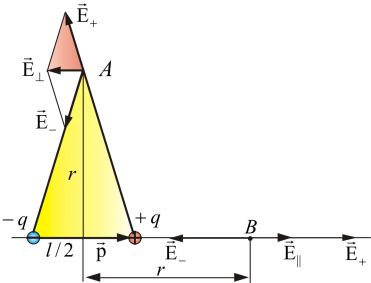 Рис.
1.6
Рис.
1.6
в точке Пример 1. Найдем Е А на прямой, проходящей через центр диполя и перпендикулярной к оси (рис. 1.6)
|
|
|
(т.к. |
(1.5.1) |
Из подобия заштрихованных треугольников можно записать:
|
|
отсюда |
( |
(1.5.2) |
Обозначим
вектор: ![]() – электрический
момент диполя (или
дипольный момент)
– произведение
положительного заряда диполя на плечо
– электрический
момент диполя (или
дипольный момент)
– произведение
положительного заряда диполя на плечо ![]() .
Направление совпадает с направлением
, т.е. от отрицательного заряда к
положительному. Тогда, учитывая
что
.
Направление совпадает с направлением
, т.е. от отрицательного заряда к
положительному. Тогда, учитывая
что ![]() получим:
получим:
|
|
или |
|
(1.5.3) |
Пример 2. На оси диполя, в точке В (рис. 1.6):
|
|
или |
( |
(1.5.4) |
Пример 3. В произвольной точке С (рис. 1.7).
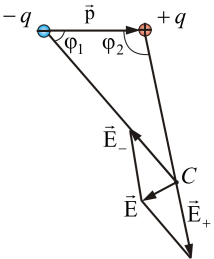 Рис.
1.7
Рис.
1.7
|
|
|
(1.5.5) |
где ![]() .
.
При ![]()
при ![]() .
.
Из приведенных примеров видно, что напряженность электрическо-го поля системы зарядов равна геометрической сумме напряженностей полей каждого из зарядов в отдельности (принцип суперпозиции).
Диполь во внешнем электрическом поле
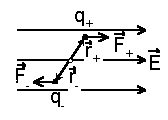
Найдем момент сил, действующих на диполь в однородном электрическом поле. Пусть положения положительного и отрицательного зарядов относительно центра диполя характеризуются векторами r+ и r- , соответственно. Тогда, в соответствии с определением момента сил, имеем
Рис. 3.4 |
Так как по определению
|
Момент сил, очевидно, равен нулю, когда векторы p и E коллинеарны, однако устойчивым положением является только такое положение, когда они еще и совпадают по направлению. В однородном поле, очевидно, F+ + F_= 0.
Если диполь находится в неоднородном внешнем электрическом поле, то равнодействующая сил, действующих на положительный и отрицательный заряды диполя оказывается не равной нулю:
|
(3.10) |
где E+ и E_ - напряженность поля в точках расположения положительного и отрицательного зарядов, соответственно, а разность E+ - E_ есть приращение вектора E на отрезке, равном длине диполя, взятом в направлении его оси. В выражение (3.10) входит так называемая производная вектора по направлению, которая в общем случае определяется довольно сложно. Рассмотрим простейший случай, когда неоднородное поле обладает симметрией относительно оси x. Пусть ось диполя также направлена вдоль оси x. Тогда сила будет иметь составляющую только вдоль оси x, равную
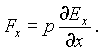
Если, например, поле убывает в направлении оси диполя, то производная в последнем выражении будет отрицательной, и диполь будет втягиваться в область более сильного поля.
Находясь во внешнем поле, диполь обладает некоторой энергией помимо энергии взаимодействия зарядов его составляющих.
Рис. 3.5 |
Пусть диполь находится в однородном электрическом поле. Направим ось x вдоль вектора E. Поскольку
то потенциальная энергия диполя будет равна |
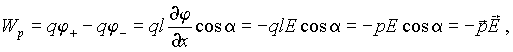
- угол между осью диполя и направлением поля.где