22. Способы задания движения точки.

Существуют 3 способа задания движения точки: естественный, координатный и векторный. Естественный способ: Если кроме траектории, на которой отмечено начало отсчета задана зависимость , то это уравнение называется законом движения точки по заданной траектории. Координатный способ: Когда траектория точки заранее неизвестна положение точки в пространстве определяется 3-мя координатами абсцисса X, ордината Y и аппликата Z (см. рис в конспекте). Функции от координат с исключением времени: ; ; . Каждая координата является функцией от времени. Эти уравнения выражают закон движения точки в прямоугольной 3хмерной система координат. В частном случае если точка движется на плоскости: ; ; ; 2-хмерное движение. Векторный способ:тДвижение задается с помощью векторов.

23. Определение скорости и ускорения точки при естественном способе задания ее движения.

Пусть за промежуток времени ∆t точка прошла путь . , значение средней скорости: ; но это значение скорости отличается от значения скорости в конкретный момент времени t. Скорость в этот момент времени: ; (см. рис в конспекте) Ускорение. Вектор , то есть ускорение точки в данный момент времени есть геометрическая сумма 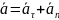; - касательное и - нормально ускорение. Вектор касательного ускорения в любой момент времени направлен по касательной поэтому называется касательным или тангенсальным ускорением. ; Вектор нормального ускорения в любо момент времени перпендикулярным касательной и равен 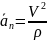. Модуль нормального ускорения – это направление угла между ускорением и скоростью находят с помощью тригонометрической функции. 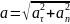; ; ; 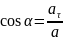. Если векторы скорости и касательного ускорения направлены в первичную сторону называется ускоренным движением. Если эти вектора направлены в разные стороны, то движение замедленно следовательно знаки разные и угол тупой.

24. Частные случаи движения точки.

1. Прямолинейное движение.

В этом случае нормальное ускорение равно нулю , то есть радиус кривизны равен ∞, и направление скорости остается неизменным. 2. Равномерное движение. 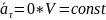; 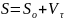- путь; . Частные случаи: Когда , - равномерное движение V=0. 3. Равномерное движение точки по окружности. Если 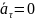, , , то получается окружность. (см. рис. В конспекте) , , если принят 4. Равнопеременное движение. Если

25. Поступательное движение. Вращательное движение. Угловая скорость и угловое ускорение

(Рисунки в конспекте) Движение твердого тела, при котором любой выбранный в теле отрезок прямой перемещается оставаясь параллельным своему первоначальному положению, называется поступательным.

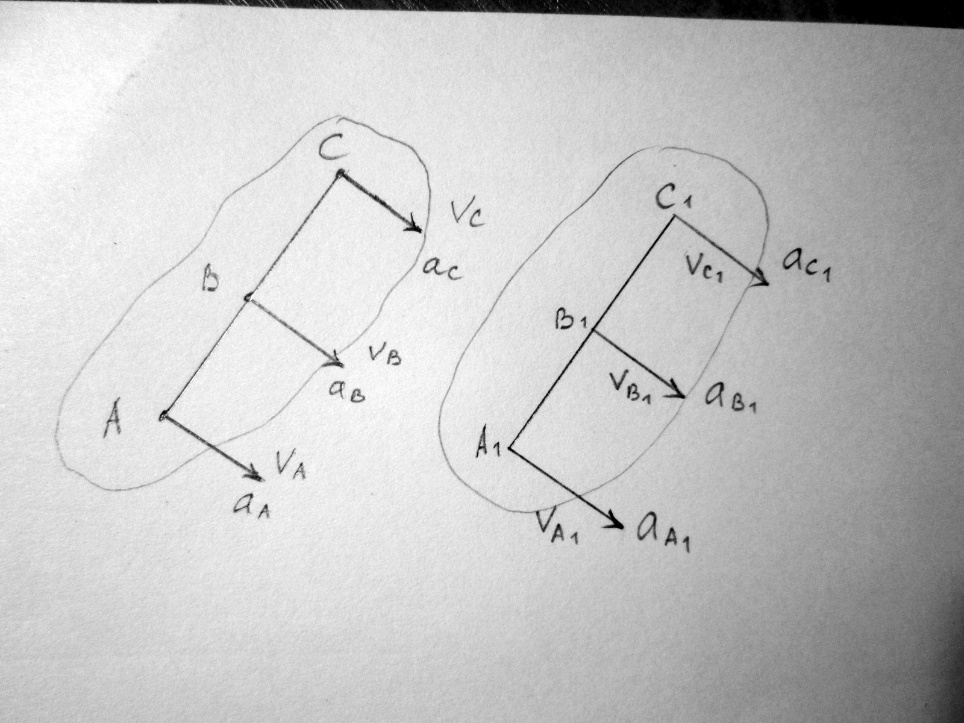V_A=V_B=V_C ;V_A1=V_B1=V_C1 ;a_A=a_B=a_C

a_A1=a_B1=a_C1

Поступательное движение твердого тела полностью характеризуется движением любой его точки.

Обычно поступательное движение тела задается движением его центра тяжести, или при поступательном движении тело можно считать материальной точкой.

Движение твердого тела, при котором все его точки перемещаются по окружностям с центрами, расположенными на перпендикулярной этим окружностям неподвижной прямой называется вращательным.

Чтобы определить положение тела в пространстве в любой момент времени, необходимо знать зависимость между углом поворота и временем, т.е. знать закон вращательного движения тела: f(t).

Угловая скорость – величина, характеризующая быстроту изменения угла поворота во времени. , рад/с=с^-1 ;

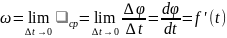
Единица измерения угловой скорости: Характеристекой быстроты изменения скорости служит угл. ускорение: , с^-2

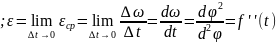
Положительным считается угол поворота, отсчитанный против хода часовой стрелки, отрицательным – по ходу.

Если векторы скорости и ускорения направлены в одну сторону, то вращательное движение называется ускоренным, если в разные – замедленным.