18. Пространственная система произвольно расположенных сил. Условие равновесия.

Это система сил произвольно раположенных в пространстве, линии действия которых не пересекаются в одной точке и не лежат в одной плоскости. Сложение пространственной системы произвольно расходящихся сил аналогично сложенного плоской системой произведения расп.сил. Если главный вектор равен нулю, то равны трём его составляющие относительно тех же осей. ∑Fix =0; ∑Fiy =0; ∑Fiz =0; Мx(Fi) = 0; Мy(Fi); Мz(Fi) = 0 Значит произвеение пространственной системы сил статически определима в том случае, когда число неизвестных не превышает шести. Если на тело действует пространство систем параллельных сил: ∑Fix =0; Мx(Fi) = 0; Му(Fi) = 0

19. Центры тяжести плоских фигур.

Центр тяжести однородной пластинки называют центром тяжести.

;

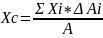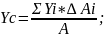
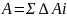
Сумма произведений или элементарных S(площадей) входящих в состав S(площади) фигуры, но это алгебраические значения их расстояния до некоторой оси называется статистическим моментом площади фигуры относительно этой оси.

;

; ;

; ;

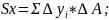
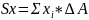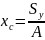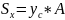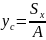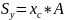Т. е. статический момент S(площади) плоской фигуры относительно оси равен площади фигуры на алгебраическое значение от расстояния от центра тяжести до этой оси.

Вспомогательные теоремы:

1. если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси;

2. если однородное тело имеет плоскую симметрию, то его сила тяжести находится в этой плоскости;

На основании этих теорем положения центра в тяжести некоторых симметричных фигур:

1. центр тяжести S круга находится в геометрическом центре;

2. центры тяжести S ромба, параллелограмма, прямоугольника и квадрата лежит на пересечении диагоналей;

3. центр тяжести правильного многоугольника находится в центре вписанного или описанного круга.

20. Определение положения центра тяжести плоской фигуры по центрам тяжести и его частей.

См. рисунок(сразу после названия темы) в конспекте. Положение плоской фигуры состоящей из 3х частей положение центров тяжести которого известно определяется по формуле: 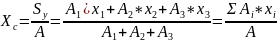; ; 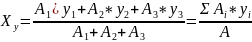Способ сложения площадей S произвольных фигур(см. рис в конспекте). 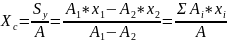; ; 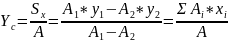Задача определения центра тяжести плоской фигуры состоящая из нескольких частей может быть представлена в виде нескольких этапов: 1.составная фигура разбивается на простейшие и вычисляются их площади. К простейшим относятся такие плоские фигуры положение центра тяжести, которых известно(прямоугольник, круг, кольцо, треугольник, и так далее) или легко определяется круговой сектор с простейшим также относительно сечения профиля стандартного проката. Стандартный прокат - уголок, тавр… 1. выбираем базовые оси координат, относительно которой с чертежами берут координаты центров тяжести каждой простейшей фигуры.

21. Основные понятия кинематики.

Раздел механики занимается изучением движения материальных тел без учета их масс и действующих на них сил называется кинематикой. Движение – это основная форма материальных тел. Покой и равновесие – это частные случаи движения. Всякое движение в том числе и механическое происходит в пространстве и во времени. Все тела состоят из материальных точек. Чтобы получить правильно о движении тела необходимо изучения движения точки. Геометрическое место положений движения точки в пространстве в рассматриваемой системе отсчета называется траекторией. По виду траектории делятся: прямолинейное; криволинейное.

См. рисунок в конспекте. При движении точка за определенный промежуток времени проходит некоторый путь L, который изменяется вдоль траектории в направлении движения: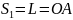 ; из рисунка, опять же см. рис. Если точка начала двигаться не из начала отсчета О, а из расположения находится на начальном расстоянии Sо, то 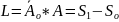; Векторная величина характеризующая в каждый данный момент времени направления и быстроту движения точки называется скорость.(см. рис. 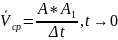конспект) Скорость точки в любой момент времени и ее движению направлена по касательной к траектории: ; Векторная величина характеризующая быстроту изменения направления и изменения числового значения скорости называется ускорение.(см. рис. В конспекте)