2.6. Преобразования как изменение систем координат
Рассмотренное преобразование множества точек, принадлежащих объекту, в некоторое другое множество точек производилось в одной и той же системе координат. Таким образом, система координат остается неизменной, а сам объект преобразуется относительно начала координат до получения желаемого результата.
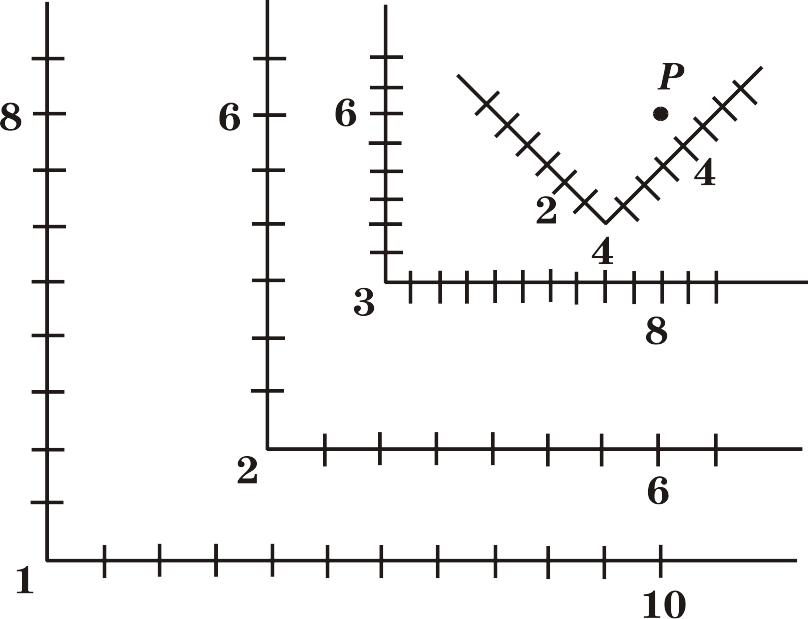
Рис. 2.11
Другим способом описания преобразования является смена систем координат. Такой подход оказывается полезным, когда желательно собрать вместе много объектов, каждый из которых описан в своей собственной локальной системе координат (ЛСК), и выразить их координаты в одной глобальной (ГСК).
Вначале рассмотрим, как положение точки, заданной в одной СК, можно описать в любой другой СК.
Точка имеет координаты:
1
СК —
;
2
СК —
;
3
СК —
;
4
СК —
.
Преобразования СК имеет вид:
1
СК — 2 СК:
;
2
СК — 3 СК:
;
3
СК — 4 СК:
.
Тогда координаты точки во 2 СК через 1 СК:
.
Обратное преобразование из 2 СК в 1 СК:
.
Причем:
.
Таким
образом, существует три способа
преобразования объектов:
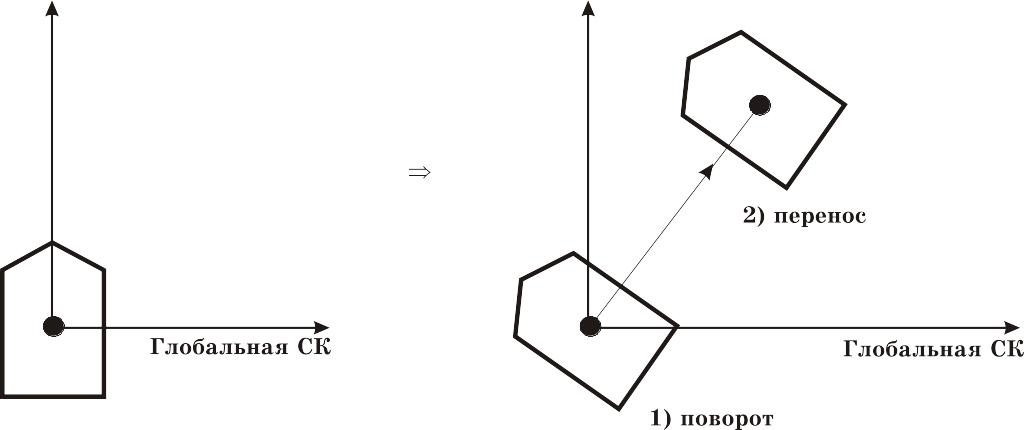
Рис. 2.12 Все объекты описаны в глобальной СК и с помощью преобразований приводятся к новым позициям в той же глобальной СК.
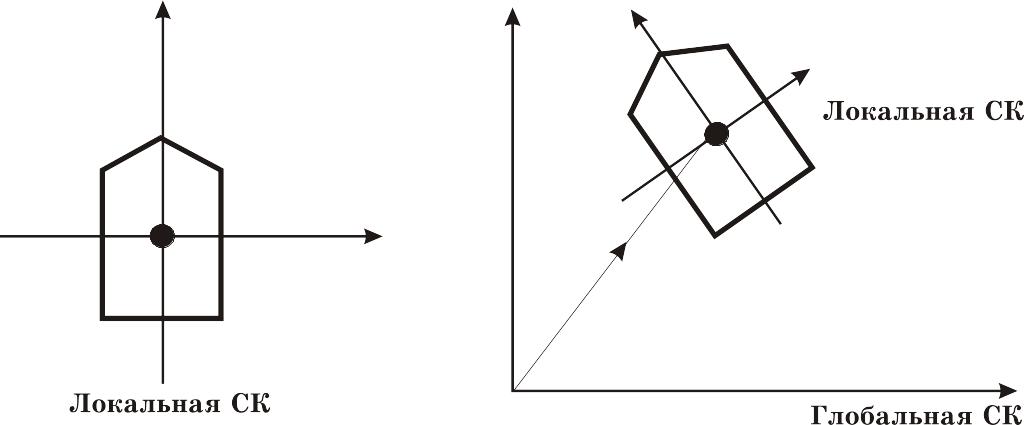
Рис. 2.13 Каждый объект задан в собственной локальной СК и затем преобразуется в глобальную СК.
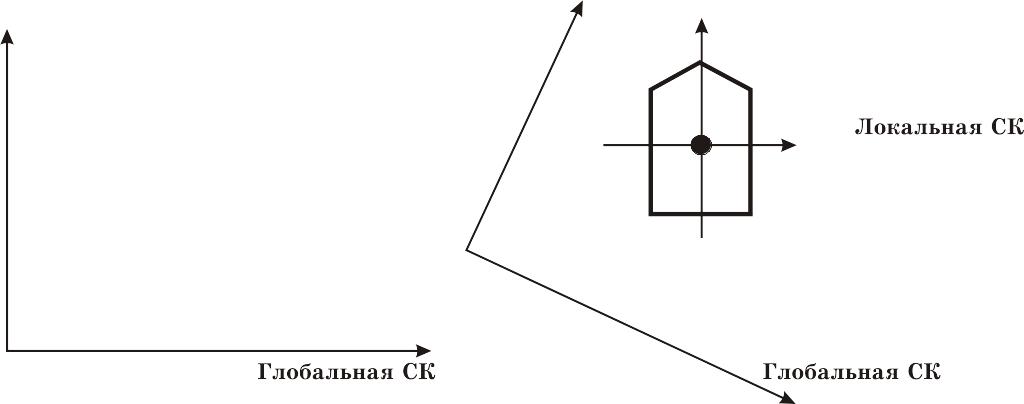
Рис. 2.14 Происходит преобразование систем координат с помощью определения новой глобальной СК относительно локальной СК.
3. Алгоритмы растровой графики
Алгоритмы развертки, применяемые при построении растрового изображения, вызывается очень часто – при каждом создании или модификации изображения. Поэтому алгоритмы должны давать не только хорошее изображение, но и делать это как можно быстрее.
Основные критерии алгоритмов:
скорость,
качество изображения.
Но обычно предпочтение отдается быстродействию.
3.1. Преобразование отрезков из векторной формы в растровую.
Главной
задачей алгоритма развертки отрезков
является вычисление координат пикселов
на двумерной растровой сетке. При решении
этой задачи будем предполагать, что
конечные т. отрезков имеют целые
координаты. Простой алгоритм заключается
в пошаговом
x,
вычислении
и высвечивании
в т.
.
Вычисление произведения
требует
и замедляет процесс разложения в растр.
Пошаговый алгоритм
Операцию
умножения можно устранить, если заметить,
что при
сводится к
,
т.е. изменение
на 1 приводит к изменению
на
(тангенс угла наклона).
Т.о.
если
,
то
,
т.е. последующие значения т. отрезка определяются, исходя из предыдущих.
Рис. 3.1
Если
,
тот шаг по
будет приводить к шагу по
.
Поэтому надо
и
поменять местами -
на 1, а
на
.
После вычисления очередной т. происходит
округление ее координат до ближайших
целых.
Алгоритм Брезенхэма
Трудности применения предыдущего метода состоят в том, что округление до целого значения требует времени, и кроме того, и должны быть вещественными числами.
Более привлекателен в этом отношении алгоритм Брезенхэма, т.к. в нем используется только целая арифметика. Вещественные переменные не используются совсем, и, значит, округление не нужно.
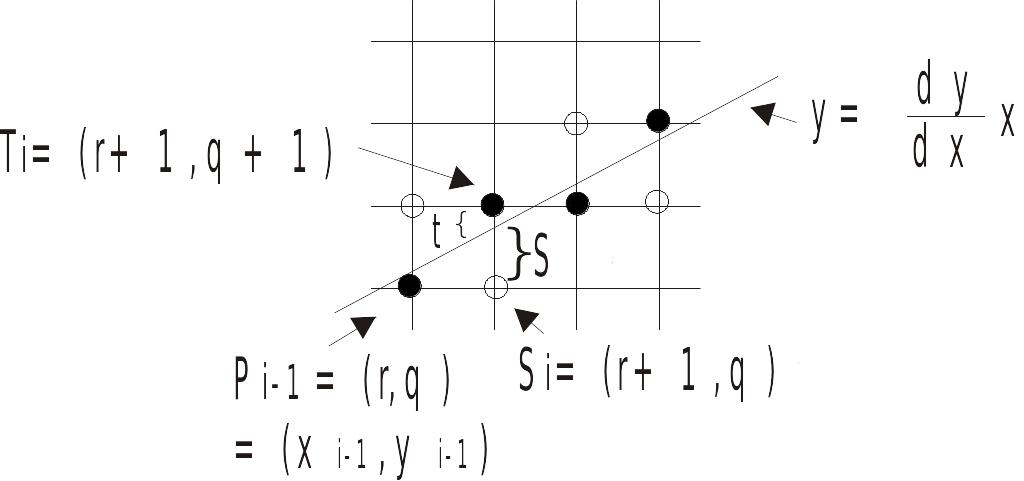
Рис. 3.2
Суть
метода: В
алгоритме используется управляющая
переменная
,
которая на каждом шаге пропорциональна
разности между
и
.
Так для т.
надо определить, какой из
будет выбран:
и
?
Если
,
то
ближе к отрезку, в противном случае
ближе будет
.
Т.е.
если
.
А теперь рассмотрим алгоритм подробнее.
Есть
отрезок
—
.
Пусть 1-я т. находится ближе к началу
координат, тогда перенесем обе точки
при помощи
так, чтобы начальная точка отрезка стала
(0,0), а конечная —
,
или
.
Уравнение
прямой будет иметь вид:
.
Обозначим
координаты после переноса т.
через
.
Тогда координаты:
Найдем разность:
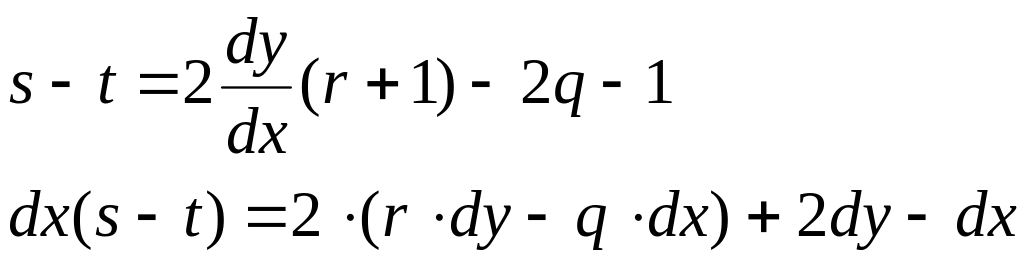
Величина
,
поэтому
можно использовать в качестве проверки
условия.
Обозначим:
,
имеем:
.
Т.к.
,
,
то
(1)
Прибавляя 1 к каждому индексу:
Вычитая
из
:
Но
(2)
Т.е.
вначале вычисляется
.
Если
,
выбирается
,
тогда
и
.
Если
,
выбирается
,
тогда
и
.
Т.о.
мы получили итерактивнй способ вычисления
по предыдущему значению
и выбора между
и
.
Начальное
значение
находят из выражения (1) при
,
:
.