2. Геометрические преобразования

2.1. Двумерные преобразования Перенос

Точки на плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса. Для каждой точки , которая перемещается в новую точку , сдвигаясь на единиц по оси и на — по оси , можно написать:

. (1)

Определим векторы-строки:

,

тогда уравнения (1):

, (2)

или кратко:

. (3)

Но объект есть множество точек. Его можно переносить, применяя уравнения (1) к каждой его точке. Но каждый отрезок состоит из бесконечного числа точек и этот процесс длился бы бесконечно долго. Удобнее все точки, принадлежащие отрезку перенести путем перемещения одних лишь крайних точек отрезка. И потом вычертить новый отрезок между ними.

Масштабирование

Т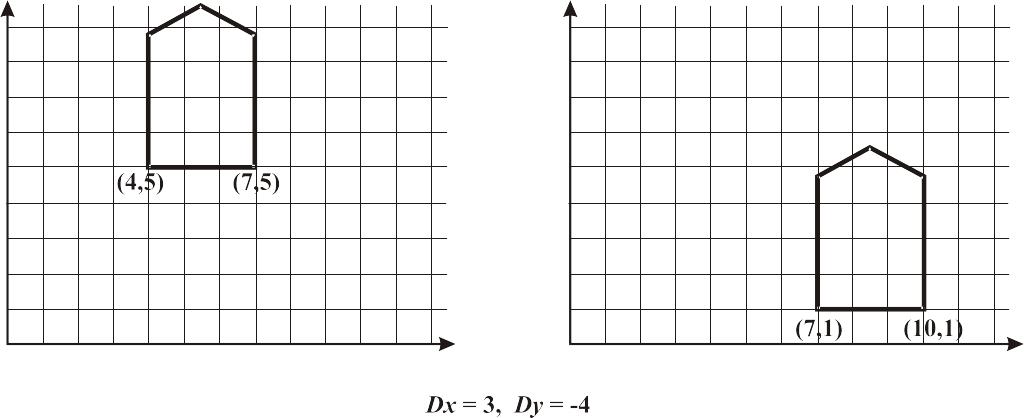 очки можно масштабировать (растянуть) в раз по оси и в — по оси .

Рис. 2.1

Получим новые точки с помощью умножения:

. (4)

Определив как:

,

можно записать в матричной форме:

(5)

или

(6)

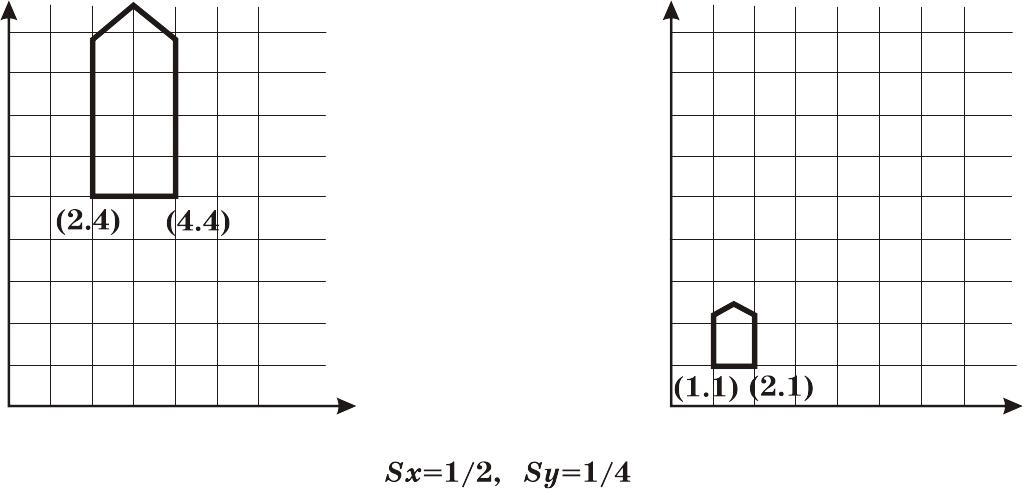
Рис. 2.2

Масштабирование производится относительно начала координат — в результате домик стал меньше и ближе к началу координат. Если бы масштабные коэффициенты были больше единицы, домик бы увеличился и отдалился бы от начала координат. Пропорции домика тоже изменились. Было применено неоднородное масштабирование, при котором . Однородное масштабирование не влияет на пропорции.

Поворот

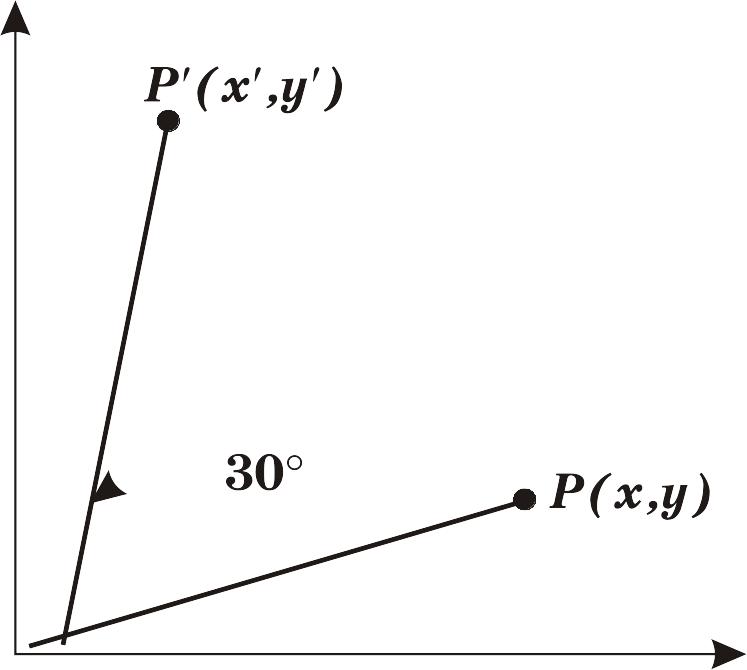Точки могут быть повернуты на угол относительно начала координат. Тогда координаты точки :

Рис. 2.3

В матричной форме:

(8)

или

(9)

где — матрица поворота.

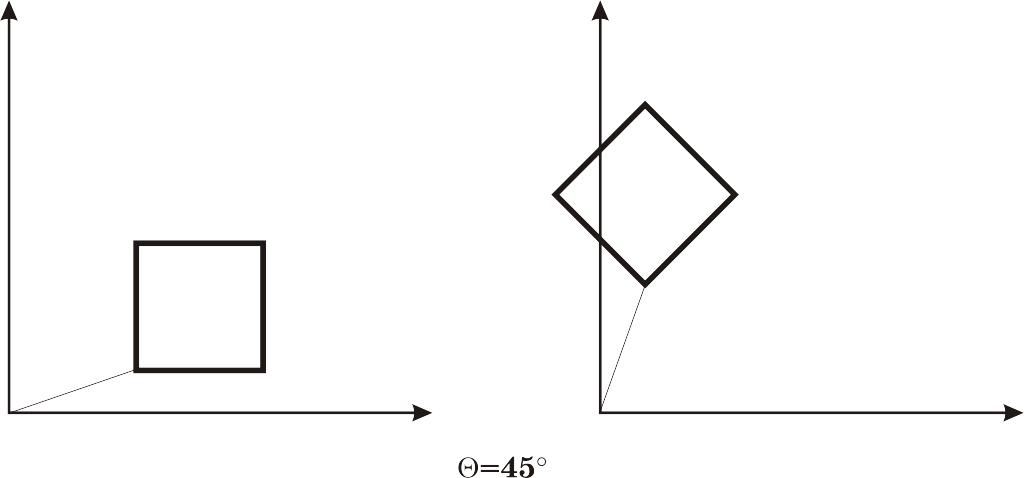
Рис. 2.4

Положительное направление — против часовой стрелки, отрицательное — по часовой стрелке.

2.2. Однородные координаты и матричное представление двумерных преобразований

Преобразования переноса, масштабирования и поворота в матричной форме имеют вид:

Перенос реализуется с помощью операции сложения, а масштабирование и поворот — операции умножения. Удобно было бы эти преобразования представить в единой форме. Рассмотрим, как это сделать.

Если мы выразим точки в однородных координатах, то все три преобразования можно реализовать с помощью операции умножения.

В однородных координатах точка записывается как , где — масштабный множитель, не равный нулю.

При этом, если точка задана в однородных координатах , то можно найти ее декартовые координаты:

Если же , то операция деления не нужна:

Перенос

Уравнение переноса (1) запишется в виде матрицы преобразования:

, (10)

или

, (11)

где

.

Перемножив, получим:

.

Докажем, что если точку перенести в на расстояние , а затем в точку на расстояние , то в результате получим перенос на расстояние .

(12)

(13)

Доказательство:

Теперь подставим (12) в (13):

.

Матричное произведение и :

то есть перенос — функция аддитивная.

Масштабирование

Уравнение масштабирования (4) в матричной форме имеет вид:

(14)

Определяя

,

имеем

. (15)

Перемножив, получим:

.

Докажем, что масштабирование — функция мультипликативная, то есть если точку промасштабировать в точку с , а потом — в точку с , то результат будет иметь вид: .

Доказательство:

(16)

(17)

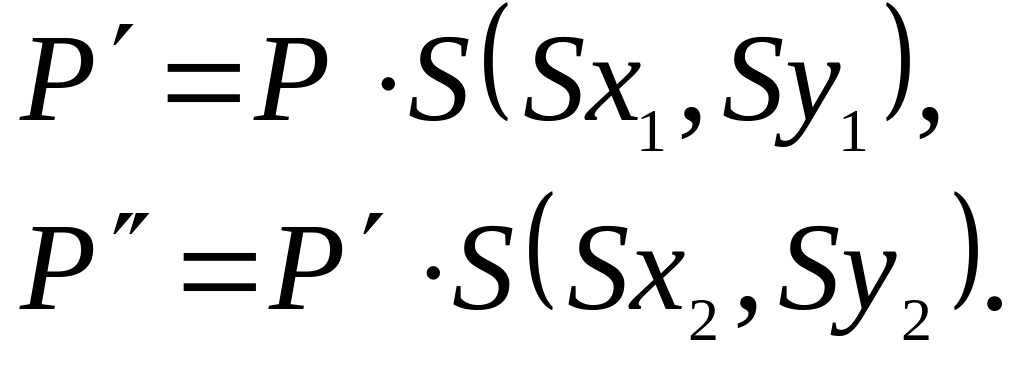
Подставляя (16) в (17):

.

Матричное произведение и :

.