13.3. Закраска полигональных сеток.

Существует 3 способа закраски объектов, заданных полигональными сетками:

Однотонная закраска

Вычисляется 1 уровень интенсивности, который используется для закраски всего многоугольника. При этом предполагается, что:

1. Источник света расположен в бесконечности ( на всей полигональной грани)

2. Наблюдатель находится в бесконечности ( на всей полигональной грани)

3. Многоугольник п.с. реальную моделируемую поверхность, а не является аппроксимацией криволинейной поверхности.

Если первое или второе условие неприемлемо, можно использовать усредненное значение , вычисленные в центре многоугольника.

Третье предположение тоже часто не выполняется, но оно оказывает большое влияние на результат: каждая из видимых граней аппроксимированной поверхности хорошо отличима от других, т.к. интенсивность каждой из этих граней отличается от интенсивности соседних граней (эффект полос Маха).

Интерполяция интенсивностей (метод Гуро)

Метод Гуро позволяет получать сглаженный объект на этапе визуализации, не внося изменения в геометрическую модель (полигональные сетки). Полосы Маха значительно уменьшаются.

Процесс закраски осуществляется в 4 этапа:

1. Вычисляются нормали к поверхностям.

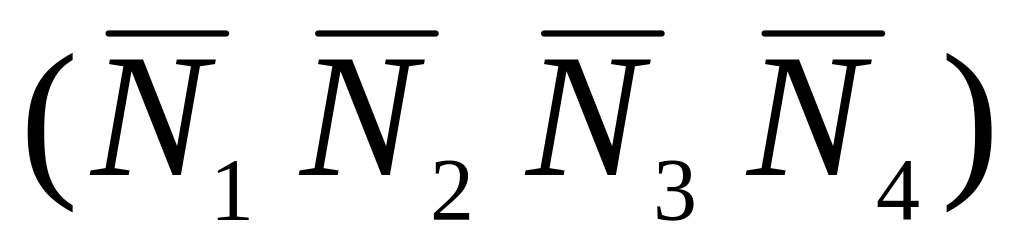
2. Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.

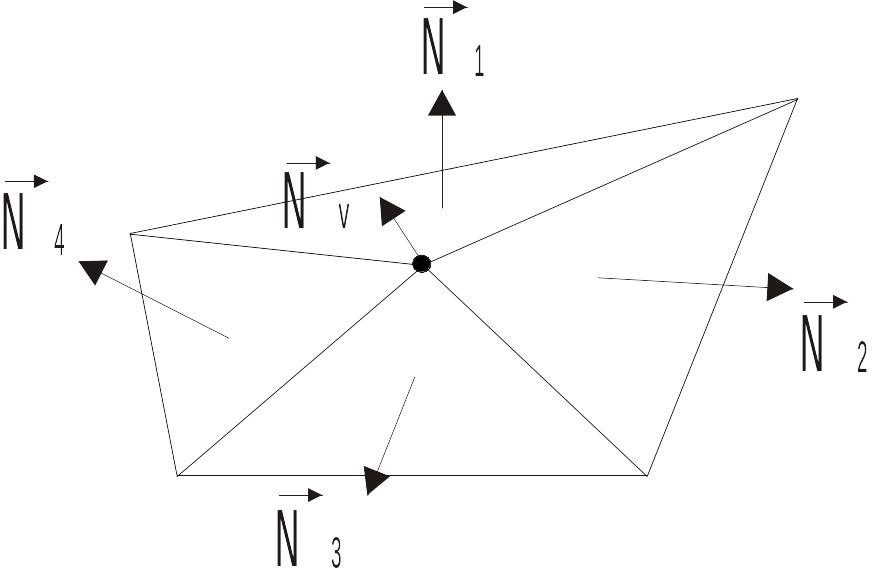
Рис. 13.12

3. Используя нормали в вершинах и применяя произвольный метод закраски, вычисляются значения в вершинах.

4. Каждый многоугольник закрашивается путем линейной интерполяции значений в вершинах сначала вдоль каждого ребра, а затем между ребрами вдоль каждой сканирующей строки:

Рис. 13.13

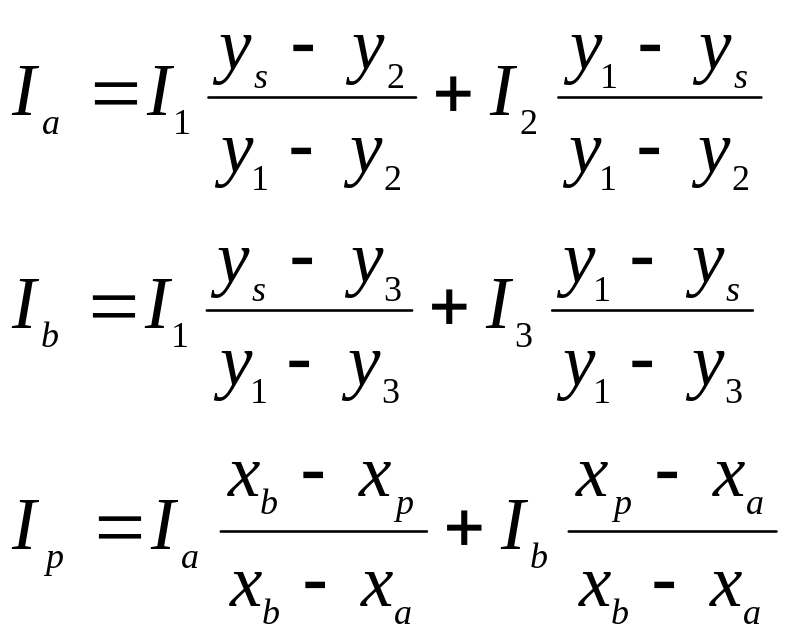
Интерполяция вдоль ребер легко объединяется с алгоритмом удаления скрытых поверхностей, построенном на принципе построчного сканирования. Для всех ребер запоминается начальное , а также изменение при каждом единичном шаге по координате y. Заполнение видимого интервала на сканирующей строке производится путем интерполяции между значениями на двух ребрах, ограничивающих интервал. Для цветных объектов отдельно интерполируется каждая из компонент цвета.

Интерполяция векторов нормали (метод Фонга)

Закраска Фонга требует больших вычислительных затрат, но она позволяет разрешить многие проблемы метода Гуро. При закраске Гуро вдоль сканирующей строки интерполируется значение , а при закраске Фонга – вектор нормали. Затем он используется в модели освещения для вычисления . При этом достигается лучшая локальная аппроксимация кривизны поверхности, и получается более реалистичное изображение. Особенно правдоподобно выглядят зеркальные блики, которые в методе Гуро сильно размываются.

Этапы закраски:

1. Вычисляются нормали к поверхностям.

2. Определяются нормали в вершинах путем усреднения нормалей по всем граням, которым принадлежит вершина.

3. Для каждой точки сканирующей строки определяется вектор нормали путем линейной интерполяции значений N (сначала в вершинах, затем - между ребрами).

4. Для каждой точки сканирующей строки вычисляется значение интенсивности .

Метод Фонга приводит к более качественным результатам, т.к. аппроксимация нормали осуществляется в каждой точке. Полосы Маха практически исчезают.