Пропускание света (прозрачность)
Поверхности могут направленно и диффузно пропускать свет. Направленное пропускание света происходит сквозь прозрачные вещества (стекло). Через них хорошо видны предметы, несмотря на то, что лучи света, как правило, преломляются, т.е. отклоняются от первоначального направления. Диффузное пропускание света происходит сквозь просвечивающиеся материалы (замерзшее стекло), в которых поверхностные неоднородности приводят к беспорядочному перемешиванию световых лучей. Поэтому очертания предмета, рассмотренного через такие материалы, размыты.
При переходе из одной среды в другую световой луч преломляется (торчащая из воды палка кажется согнутой). Преломление рассчитывается по закону Снеллиуса: падающий и преломляющий лучи лежат в одной плоскости, а углы падения и преломления определяются:
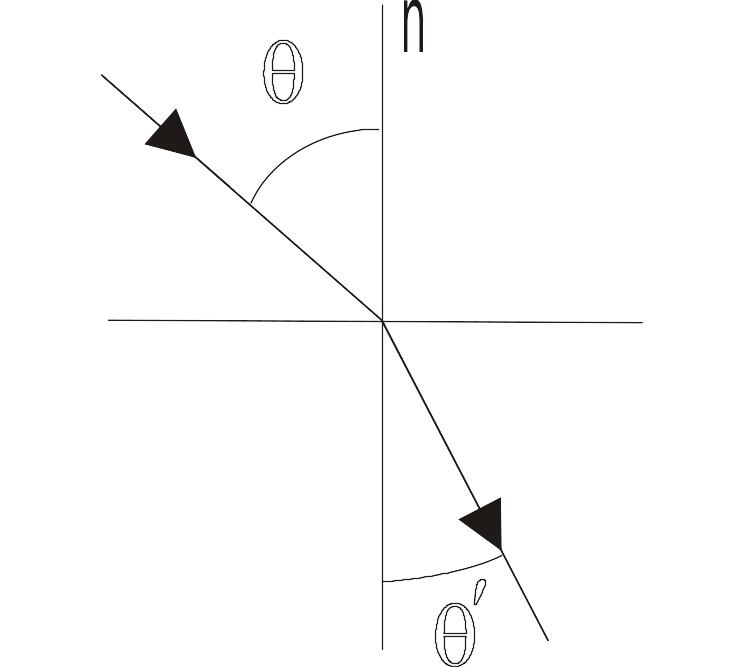
Рис. 13.9
-
показатели преломления двух сред.
Моделирование
пропускания света осуществлялось
несколькими способами. В простейшем из
них преломление не учитывалось совсем
и световые лучи пересекают поверхность
без изменения направления. Т.о. все, что
видимо на луче зрения при его прохождении
через прозрачную поверхность, геометрически
также принадлежит этому лучу. При наличии
преломления геометрический и оптический
лучи зрения не совпадают. Без учета
преломления виден предмет В, с преломлением
– А. На 1-ый взгляд достаточно знать
угловые соотношения в точках пересечения
луча с объектом. Но это не так, т.к. длина
пути луча в объекте тоже меняется,
1) не совпадают т. выхода луча из объекта;
2) меняется количество поглощенного
объектом света, поэтому исходящий луч
имеет другую интенсивность.
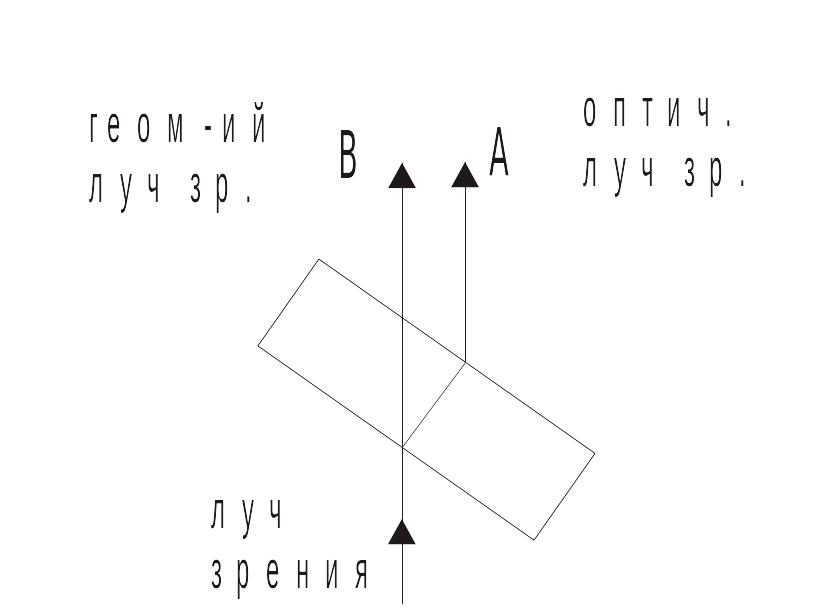
Рис. 13.10
Простое пропускание света можно встроить в любой алгоритм удаления невидимых поверхностей, кроме z – буфера, т.к. поверхности в нем обрабатываются в произвольном порядке. Если используется алгоритм построчного сканирования и передний многоугольник оказывается прозрачным, определяется ближайший из др. многоугольников, внутри которых находится сканирующая строка. Уровень закраски определяется как взвешенная сумма уровней, вычисленных для каждого из двух многоугольников:
— интенсивность
видимой поверхности,
— интенсивность
поверхности за видимой,
— коэффициент
прозрачности поверхности 1 (
полная
прозрачность
полная
непрозрачность).
Если тоже прозрачна, то алгоритм применяется рекуррентно, пока не встретится непрозрачная поверхность или фон.
При расчете общей интенсивности обычно используется направленный пропущенный свет, поскольку учет диффузного вызывает много сложностей. Поэтому моделируются только прозрачные вещества.
Общий вид модели освещения:
,
где а – рассеянный свет, d – диффузноотраженный свет, s - зеркальноотраженный свет, t – пропущенный свет.
Без освещения с рассеянным светом с рассеянным и диффузным с рассеянным, диффузным и зеркальным
Рис. 13.11
Специальные модели
Для исследования общих закономерностей отражения поверхностей сложной структуры используют специальные модели:
Модель Торрэнса-Спэрроу (фацентная модель).
Поверхность представляется в виде совокупности случайно ориентированных микроскопических зеркальных граней. Отражение от каждой микрограни определяется по формуле, затем методами геометрической оптики учитывается затенение микрограней соседними и маскирование части зеркально отраженного света соседними микрогранями. Эта модель позволяет в аналитической форме учесть длину волны и угол падения лучей.
2) Модель слоистая используется для растительности, покрытой листвой. Каждый слой образован отдельными, в общем случае не перекрывающимися площадками определенных форм и размеров и обладающими ортотропным отражением. Отражение определяется затенением отражающих площадок нижних слоев вышележащими. Получить аналитическое решение такой модели сложно, обычно используют метод Монте-Карло. Результаты моделирования показывают, что поверхности такой структуры обладают обратным отражением.
Модели, основанные на статистическом описании структуры отражающих поверхностей, сложны. Это очень ограничивает их применение в машинной графике. Обычно используют приближенные модели. Полагают, что форма индикатрисы отражения не зависит от длины волны.