4.4 Отсечение многоугольников

Ранее рассмотрено отсечение отрезков. Многоугольник можно рассмотреть как набор отрезков в том случае, если это контурное изображение. В таком случае исходная фигура может превратиться в один или более открытых многоугольников или просто стать совокупностью отдельных отрезков (рис.):

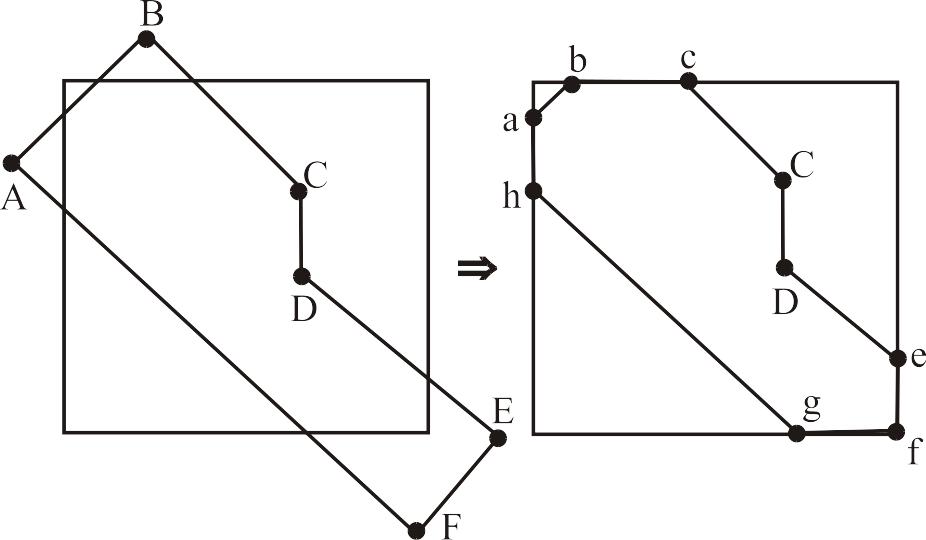
Рис. 4.7

Но если многоугольники рассматриваются как сплошные области, необходимо, чтобы замкнутость сохранялась и у результата, то есть отрезки bc, ef, fg, ha, должны быть добавлены к описанию результирующего многоугольника. Добавление ef и fg вызывает особые трудности. Много сложностей возникает и тогда, когда результат отсечения представляет собой несколько несвязанных областей.

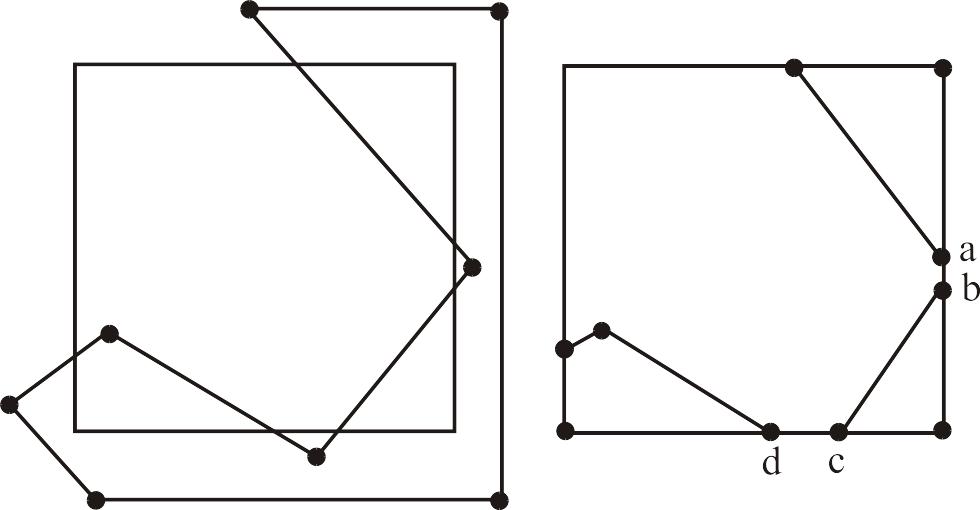
Рис. 4.8

Иногда отрезок ab и cd включается в описание результата. И если исходный многоугольник красный на синем фоне, то отрезок ab и cd тоже будут красными на синем фоне, что противоречит ожидаемому результату.

Алгоритм Сазерленда-Ходжмена для отсечения многоугольника.

В этом алгоритме исходный и каждый промежуточный многоугольник отсекаются последовательно относительно одной прямой. Исходный многоугольник задается списком вершин:

,

который порождает список его ребер:

.

Шаги алгоритма на рис.:

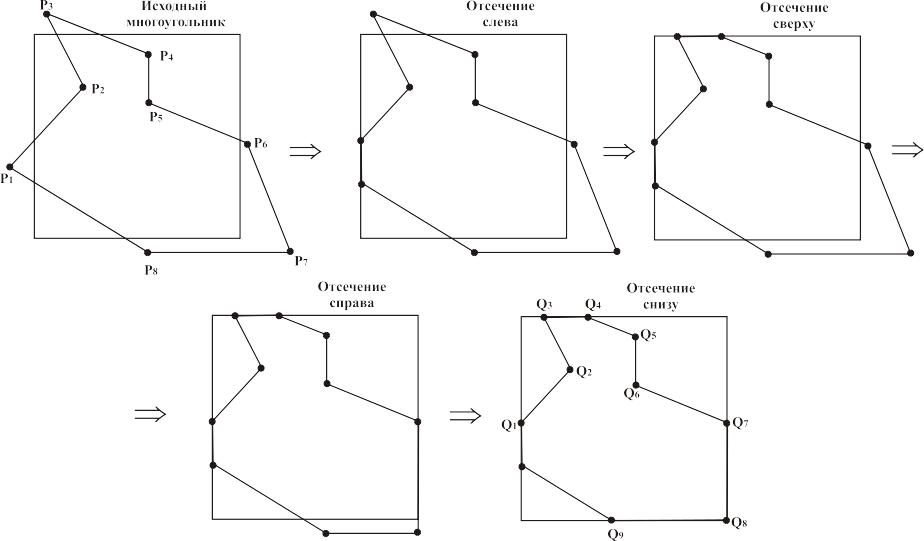
Рис. 4.9

Добавление точки Q₈ теперь стало тривиальным. Этот алгоритм может отсекать любой многоугольник (выпуклый и невыпуклый, плоский и неплоский) относительно любого окна, являющегося выпуклым многоугольником. Порядок отсечения многоугольника разными сторонами непринципиален. Результат работы алгоритма — список новых вершин многоугольника. Так как каждая сторона многоугольника отсекается независимо от других, то достаточно рассмотреть только возможные ситуации расположения одного отрезка относительно одной отсекающей плоскости.

Рассмотрим каждую точку Р из списка, за исключением первой, как конечную точку ребра, начальной точкой S которого является предыдущая Р_i-1 точка в этом списке. Возможны четыре ситуации расположения ребра и отсекающей плоскости:

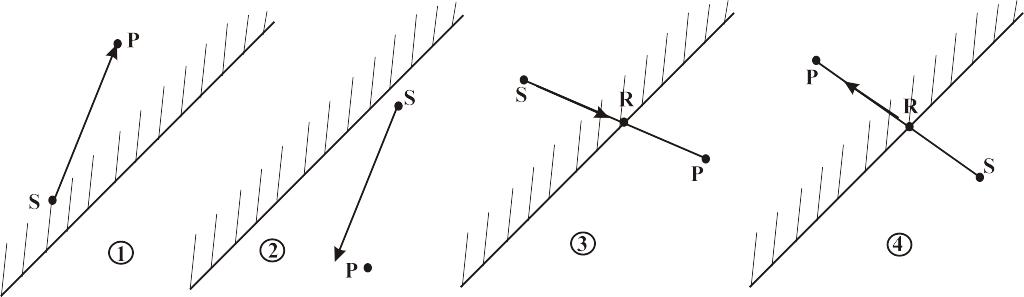
Рис. 4.10

Результатом будет занесение в список вершин результирующего усеченного многоугольника нуля, одной или двух вершин.

• Полная видимость. Результат — вершина Р (1 точка) (заносить в результат начальную точку S не надо, так как если вершины рассматриваются поочередно, то точка S уже была конечной точкой предыдущего ребра и уже попала в результат).

• Полная невидимость. Результат — 0 точек.

• Выход из области видимости. Результат — точка R (1 точка).

• Вход в область видимости. Результат — точки R, P (2 точки) (так как конечная вершина Р видима, она тоже должна попасть в результат).

Для первой вершины многоугольника надо определить только факт ее видимости. Если вершина видима, то она попадает в результат и становиться начальной точкой S. Если же вершина невидима, она тоже становится начальной точкой, но в результат не попадает.

4.5 Отсечение литер

Литеры или текст можно генерировать программно или аппаратно. Они могут состоять из отдельных отрезков (штрихов) или быть образованными точечной матрицей.

Штриховые литеры, сгенерированные программно, можно обрабатывать как любые отрезки: поворачивать, переносить, масштабировать, отсекать по любым окнам, используя рассмотренные ранее алгоритмы.

Рис. 4.11

Программно сгенерированные символы в форме точечной матрицы можно обрабатывать также. Если прямоугольная оболочка литеры пересекается с окном, то надо проверить, будет ли каждый маски символа находится внутри окна. В этом случае этот активизируется, иначе — нет.

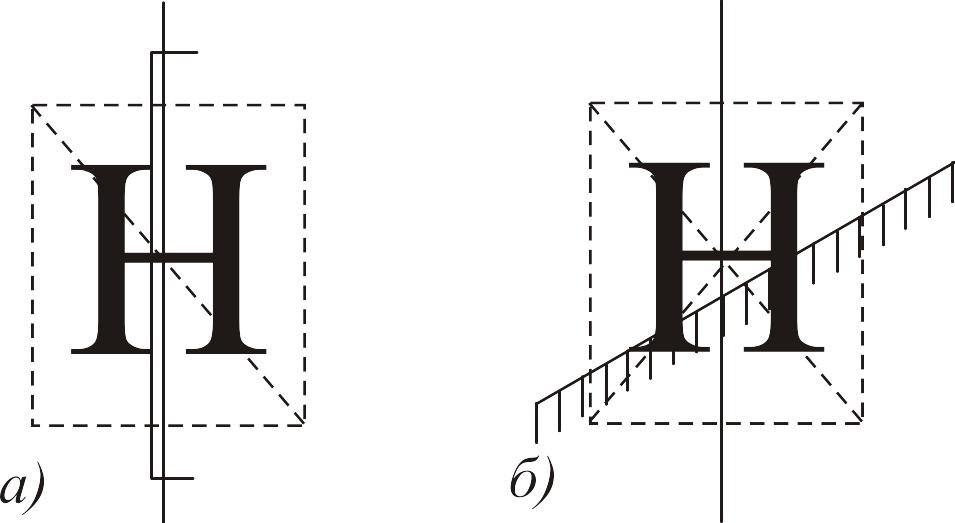
Рис.4.12

Литер складывается больше ограничений. Обычно любая не полностью видимая литера удаляется (для этого сравнивается прямоугольная оболочка литеры с границами окна). Если прямоугольная оболочка литеры ориентировано так же, как и граница окна (рис. а), то тест видимости можно провести только для одной из диагоналей оболочки. Если прямоугольная оболочка литеры ориентирована иначе, чем окно, то тесты видимости надо провести для двух диагоналей (рис. б).