4.2. Алгоритм разбиения средней точкой

В предыдущем алгоритме надо было вычислить пересечение отрезка со стороной окна. Этого можно избежать, если реализовать двоичный поиск такого пересечения путем деления отрезка его средней точкой. Алгоритм был предложен Спруллом и Сазерлендом. Программная реализация его медленнее, но аппаратная быстрее и эффективнее, так как аппаратно сложение и деление на 2 очень быстры (деление на 2 эквивалентно сдвигу побитовому вправо: 6=0110, 3=0011).

Рис. 4.4

В алгоритме используются коды концов отрезка и проверки, выявляющие полную видимость (отрезок а) и тривиальную невидимость (отрезок в). Остальные отрезки, не определяемые тривиально, разбиваются на 2 равные части. Затем те же проверки применяются к каждой из половин до тех пор, пока не будет обнаружено пересечение со стороной окна или длина разделяемого отрезка не станет пренебрежительно малой, то есть пока он не выродится в точку. После вырождения определяется видимость полученной точки. Максимальное число разбиений пропорционально точности задания координат концов отрезка.

Рассмотрим отрезок с. Хотя он невидим, он пересекает диагональную прямую окна и не может быть тривиально отвергнут. Разбиение его средней точкой 3 позволяет тривиально исключать половину 3-2, а половина 1-3 тоже пересекает диагональ окна. Делим 1-3 пополам точкой 4 и отвергаем невидимый отрезок 1-4. разбиение отрезка 3-4 продолжается до тех пор, пока не будет найдено пересечение этого отрезка с правой стороной окна. Затем исследуется обнаруженная точка и она оказывается невидимой, следовательно весь отрезок невидим.

Рассмотрим отрезок d. Он также не определяется тривиально. Разбиение его средней точкой 3 приводит к одинаковым результатам для обоих половин. Разобьем отрезок 3-2 пополам точкой 4. Отрезок 3-4 полностью видим, а отрезок 4-2 видим частично. Отрезок 3-4 можно было бы начертить, но это привело бы к неэффективному изображению видимой части отрезка (серия коротких кусков). Поэтому точка 4 запоминается как текущая видимая точка, которая наиболее удалена от точки 1. А разбиение отрезка 4-2 продолжается. Как только обнаружится видимая средняя точка, она объявляется текущей наиболее удаленной от точки 1, до тех про, пока не будет обнаружено пересечение с нижней стороной окна с заранее заданной точностью. Это пересечение и будет объявлено самой удаленной от точки 1 видимой точкой. Затем точно также обрабатывается отрезок 1-3. Наиболее удаленной от точки 2 видимой точкой будет его пересечение с левой стороной окна.

Таким образом, для отрезков, подобных d, реализуется 2 двоичных поиска двух видимых точек, наиболее удаленных от концов отрезка. Это точка пересечения отрезка со сторонами окна. Для отрезков типа е один из двух поисков не нужен.

4.3 Трехмерное отсечение отрезков

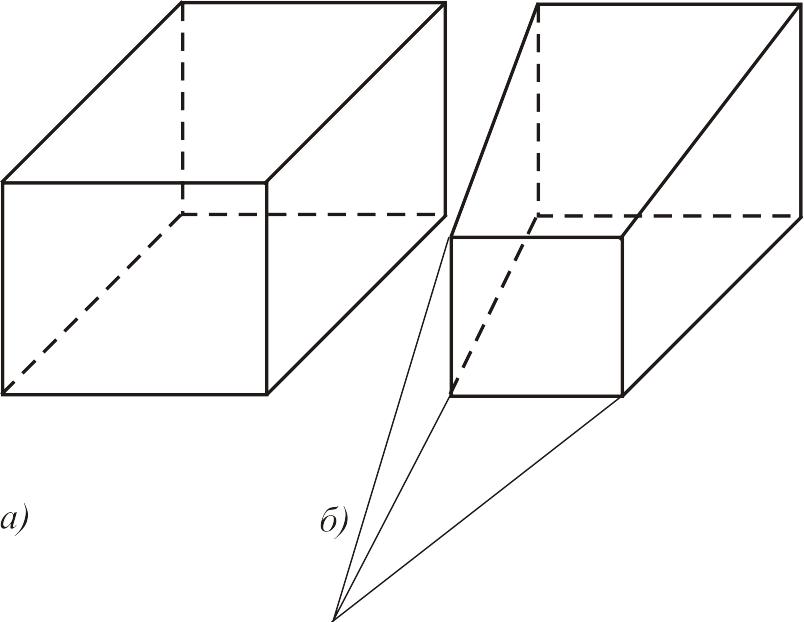
Рис. 4.5

Существуют 2 наиболее распространенные формы трехмерных отсекателей:

• Прямоугольный параллелепипед (см. рис а);

• усеченная пирамида. (см. рис б);

У каждой из них 6 граней. Для определения видимости отрезков обобщим алгоритм, используемый для двумерного случая. В трехмерном случае используется 6-битовый код: .

— если конец отрезка левее объема;

— если конец отрезка правее объема;

— если конец отрезка ниже объема;

— если конец отрезка выше объема;

— если конец отрезка ближе объема;

— если конец отрезка дальше объема.

В противном случае в соответствующие биты заносятся нули.

Далее производится анализ кодов.

• если коды обоих концов отрезка равны 0, то оба конца видимы и отрезок тоже будет полностью видим;

• если коды содержат единичный бит в одной и той же позиции, то отрезок полностью невидим.

В остальных случаях отрезок может быть частично видим или полностью невидим. Необходимо определить пересечения отрезка с гранями отсекающего объема.

Поиск точки пересечения с гранями параллелепипеда является обобщением соответствующего двумерного алгоритма.

Сложнее ситуация, когда отсекатель — усеченная пирамида.

Вид усеченной пирамиды сверху:

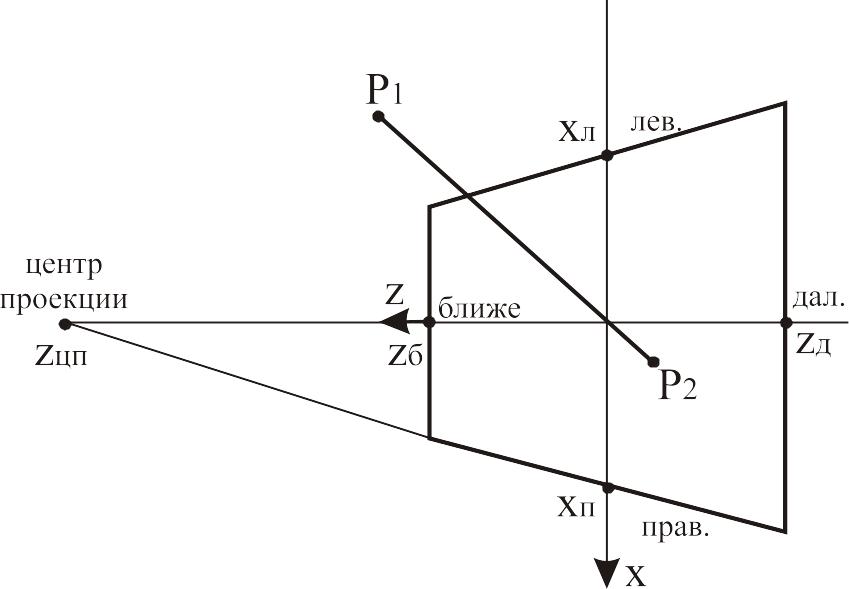
Рис. 4.6

Теперь легко найти уравнение прямой на плоскости XZ, несущей проекцию правой грани отсекателя:

,

где .

Зная это уравнение, можно определить местоположение точки: справа (вне), на, или слева (внутри) от прямой. Подстановка координат x и z точки Р в функцию правой грани, дает результат:

	>0, если Р справа от плоскости
	=0, если Р на плоскости
	<0, если Р слева от плоскости

Аналогично находятся функции для других 5 граней.

	>0, если Р справа от плоскости
	=0, если Р на плоскости
	<0, если Р слева от плоскости

	>0, если Р выше плоскости
	=0, если Р на плоскости
	<0, если Р ниже плоскости

	>0, если Р выше плоскости
	=0, если Р на плоскости
	<0, если Р ниже плоскости

	>0, если Р ближе к плоскости
	=0, если Р на плоскости
	<0, если Р дальше от плоскости
	>0, если Р ближе к плоскости
	=0, если Р на плоскости
	<0, если Р дальше от плоскости

При , формы отсекателя стремятся к прямоугольному параллелепипеду, функции стремятся к функциям прямого параллелепипеда.

Неточности могут возникнуть, если концы отрезка лежат за центром проекции, . Для этого необходимо обратить значения первых четырех битов кода.