Когерентность ребер

Принцип когерентности ребер: если ребро пересекается строкой i, то велика вероятность, что оно будет пересекаться и (i+1) – ой строкой.

,

,

Алгоритм: Создается таблица ребер (ТР), в которой все ребра сортируются по увеличению y – координаты. В ней содержатся все ребра и каждое ребро представлено в виде:

На основе ТР создается ТАР (таблица активных ребер), которая содержит только текущие ребра для каждой сканирующей строки. Они сортируются по увеличению x – координаты.

Каждое ребро представлено в виде:

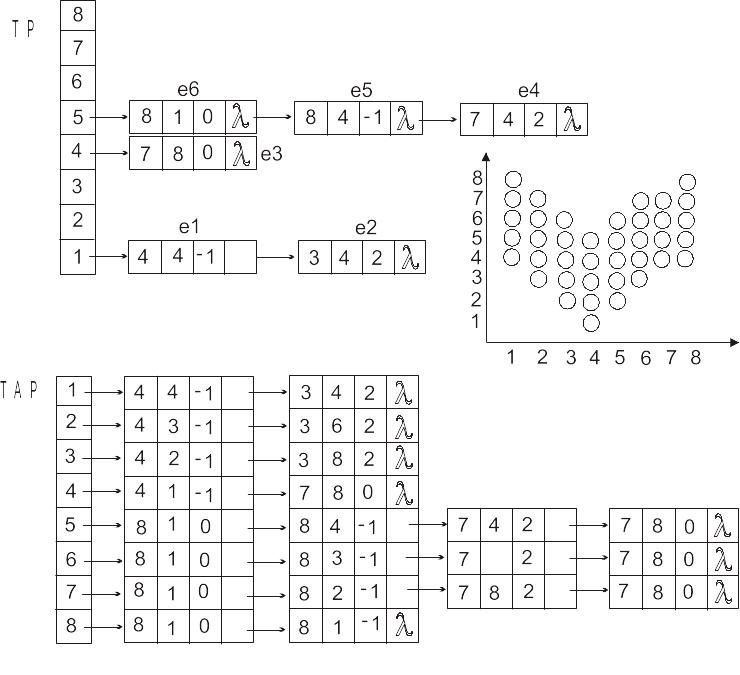
Рис. 3.26

Алгоритм создания ТАР:

1. Установить y=min – ому значению координаты y среди элементов ТР.

2. Инициализировать ТАР, сделать ее пустой.

3. Повторять шаг 3 до тех пор, пока ТАР и ТР не станут пустыми.

• Слить информацию из группы у таблицы ребер (ТР) с информацией в ТАР, сохраняя упорядочивание по x – координате.

• Занести желаемые значения в на сканирующей строке, определяемой текущим значением y, используя пары x – координат из ТАР.

• Удалить из ТАР те элементы, которые .

• Для всех элементов, содержащихся в ТАР, заменить x на .

• Т.к. на предыдущем шаге могла нарушиться упорядоченность ТАР по x, провести пересортировку ТАР.

• Увеличить y на 1 и т.о. перейти к следующей сканирующей строке.

4. Отсечение линий

4.1. Алгоритм Коэна-Сазерленда

В процессе работы с ГС пользователь формирует графические объекты произвольных размеров и сложности в СК наблюдателя. Используемые графические устройства имеют фиксированные границы (обычно прямоугольные). Иногда надо задать некоторую прямоугольную область на экране, которая определяет размеры желаемого изображения. Эта область называется областью вывода. Следовательно, попадание частей объекта за пределы области вывода может привести к определенным затруднениям. Иногда не попадающие полностью в область вывода линии просто не вычерчиваются, но это не всегда приемлемо. Поэтому приходится отсекать части отрезков прямых линий, выходящих за пределы области.

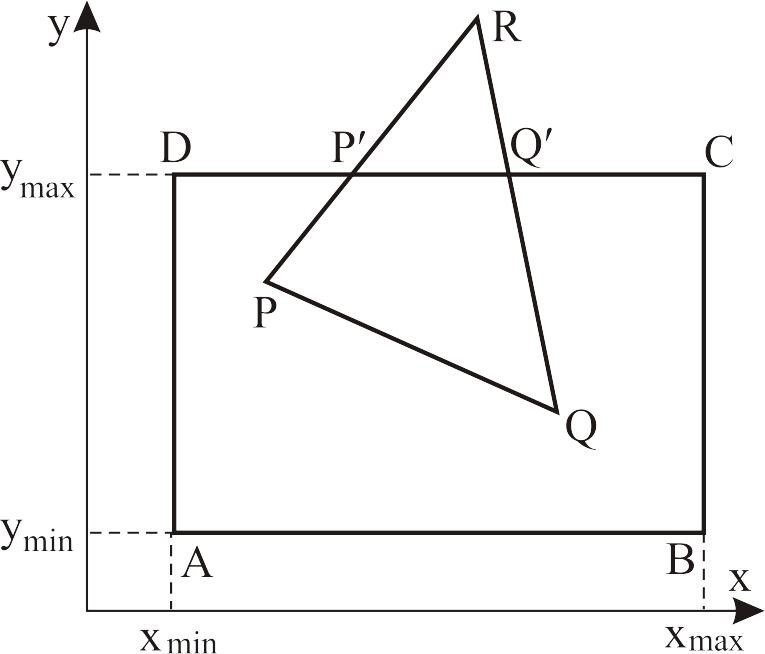
Рис. 4.1

Рассмотрим прямоугольник АВСD, который является окном (областью вывода). Все видимые отрезки прямых линий должны лежать внутри окна. Процесс отсечения должен выполнятся автоматически. Команды на вычерчивание треугольника PRQ интерпретируются как команды на вычерчивание отрезков .

Координаты точек и неизвестны. Их надо вычислить, зная координаты точек P, Q и R. Наклон отрезка PR вычисляется следующим образом:

Мы рассмотрели ситуацию, когда Р находится внутри окна, а R — удовлетворяет неравенствам:

Однако необходимо рассмотреть значительно больше ситуаций. Большое разнообразие логических операций, которые надо выполнять для решения этой задачи, делают проблему отсечения линий очень интересной с алгоритмической точки зрения. Коэн и Сазерленд разработали алгоритм для отсечения отрезков прямых линий. Его суть в том, что конечным точкам отрезка ставится в соответствие некоторый четырехбитовый код:

где может быть либо 0 либо 1. Этот код содержит информацию о положении точки Р относительно окна.

1001	0001	0101	=0,	если
1000	0000	0100	=1,	если
1010	0010	0110	=0,	если
			=1,	если
			=0,	если
			=1,	если
			=0,	если
			=1,	если

Возможны 9 из 16 битовые комбинации показаны на рисунке.

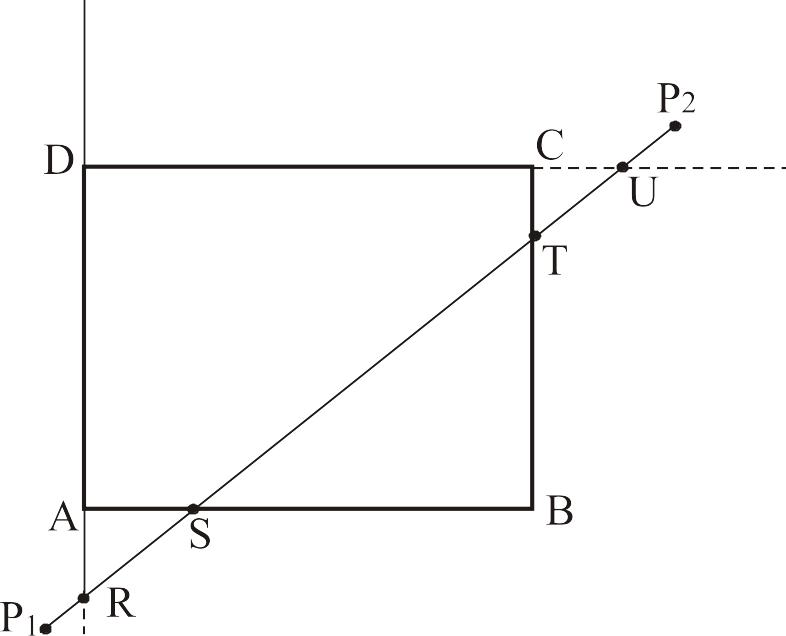
Рис. 4.2

Пусть для отрезка получены коды: .

• Если коды содержат только 0, то целиком лежит внутри окна и должен быть начерчен полностью.

• Если коды содержат единичный бит в одной и той же позиции, то отрезок целиком лежит за границами окна и не вычерчивается.

Остальные случаи рассмотрим подробнее. Если хотя бы 1 из кодов содержит единичный бит, то либо , либо перемещаются из области вне окна к одной их границ окна или к ее продолжению (точка перемещается в точку R, точка — в точку U). В последнем случае точка по-прежнему будет находится вне окна и понадобится еще одно перемещение (точка R переместиться в точку S, точка U — в точку Т). Таким образом, процесс отсечения может быть многоступенчатым, на каждом шаге расстояние между точками и уменьшатся. Процесс завершается, как только обе точки окажутся в пределах окна (код 0000). Оставшаяся часть отрезка будет вычерчена (ST),

Пример.

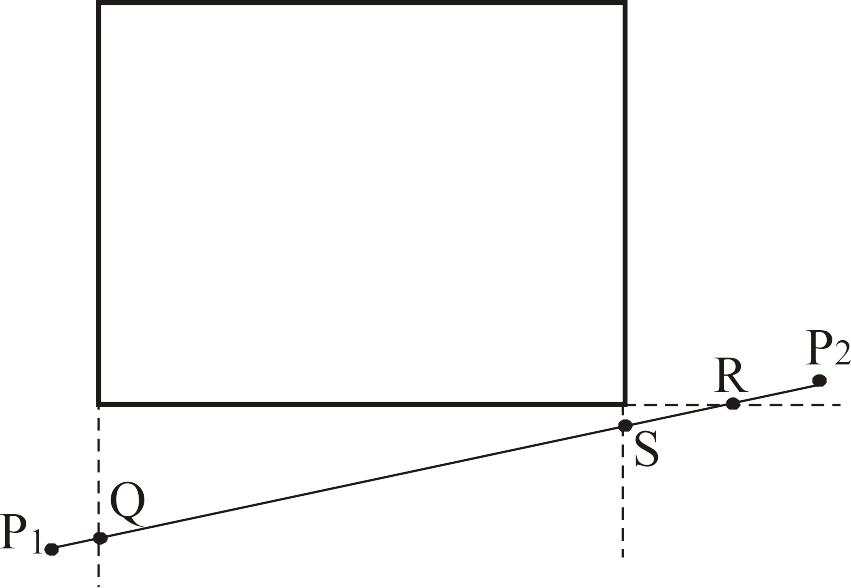
Рис. 4.3

Так как расположение отрезка не соответствует рассмотренным двум случаям, то проводится отсечение. Точка перемещается в точку Q.

Требуется дальнейшее отсечение,

,

Теперь условие соответствует случаю 2, и обе точки находятся ниже окна. Следовательно, отрезок (или его усеченный вид QR) чертить не надо.