5.4.4. Синтез цифровых систем управления с обратной связью по состоянию и динамической обратной связью по выходу

Рассмотренные выше методы синтеза с использованием обратной связи по состоянию и обратной связи по выходу применяются при проектировании цифровых систем стабилизации. Соответствующим выбором собственных значений замкнутой системы можно обеспечить заданный характер свободного движения переменных состояния. Если же проектируется система, предназначенная для отслеживания определенного входного сигнала, то обратная связь по состоянию и по выходу должна быть организована несколько иначе. Поскольку обратная связь по состоянию и по выходу не повышает порядок системы, то в общем случае нет гарантии, что выходные переменные или переменные состояния системы в установившемся режиме будут отслеживать входной сигнал.

Рассмотрим цифровую систему управления, описываемую следующими уравнениями динамики:

(5.121)

(5.122)

где х(k) – n-мерный вектор (состояние); u(k) – r-мерный вектор (вход); с(k) – р-мерный вектор (выход);  – q-мерный вектор (возмущение). Размерность матриц А, В, D, E, F и Н определяется количеством соответствующих переменных. Вектор возмущения w предполагается постоянным. В качестве компонентов вектора w могут фигурировать также входные воздействия, в соответствии с которыми должно меняться состояние системы или ее выход. Компоненты вектора w, играющие роль возмущений, в общем случае неизвестны, хотя их значения предполагаются постоянными.

Цель синтеза цифровой системы управления, описываемой уравнениями (5.121) и (5.122), можно сформулировать следующим образом: найти такое управление u(k), чтобы

(5.123)

(5.124)

Условие (5.123) эквивалентно требованию асимптотической устойчивости системы, а условие (5.124) предполагает стабилизацию выходных переменных системы. Вектор выхода с(k) не обязательно должен включать в себя только выходные переменные системы. В действительности, конструируя надлежащим образом вектор c(k), можно сформулировать большое количество задач стабилизации и слежения.

Образуем векторы приращения состояния и управления:

(5.125)

(5.126)

Тогда в соответствии с (5.125)

(5.127)

Из уравнений (5.121) и (5.122) имеем

(5.128)

(5.129)

Сформируем вектор разности между у(k + 1) и у(k):

(5.130)

где I_n – единичная матрица размерностью n  п.

Преобразуя уравнение (5.130), запишем его в виде

(5.131)

Таким образом, цель синтеза, определяемая условиями (5.123) и (5.124), эквивалентна переводу системы с уравнением (5.131) из любого начального состояния у(0) в состояние у(k)  0 при k  .

Условия управляемости. Для достижения сформулированной выше цели управления прежде всего необходимо исследовать управляемость системы, описываемой уравнением (5.131).

Обозначим:

Тогда запишем уравнение (5.131) в виде

(5.132)

Чтобы пара матриц была полностью управляемой, необходимо и достаточно обеспечить матрице

размерностью (n + p)  (n + p + r) ранг (n + p) при значениях , равных каждому из собственных значений матрицы . Итак,

(5.133)

где I_m – единичная матрица размерностью m  m. Из последнего уравнения следует, что имеет, по крайней мере, р собственных значений

 =1. Если  = 1, то (5.133) примет вид

(5.134)

Если   1, то ранг (  1)I_m равен р, и, чтобы матрица имела ранг n + p, матрица должна иметь ранг n, в предположении, что пара [A, B] управляема. Таким образом, пара матриц [ , B] будет управляемой, если:

1) управляема пара [A, B];

2) матрица 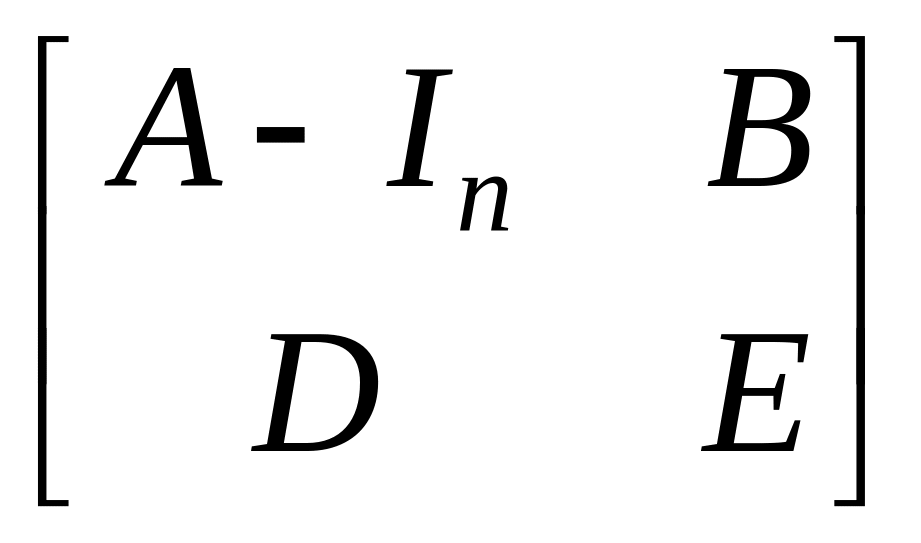имеет ранг n + p.

В результате условие управляемости системы в приращениях (5.131) выражено через матрицы коэффициентов исходной системы.

Теперь предположим, что вектор управления v(k) образуется с помощью обратной связи по состоянию, т. е.

v(k) = Gy(k) (5.135)

где G – матрица обратной связи размерностью r  (n + p), элементы которой представляют собой постоянные коэффициенты.

Учитывая выражение для v(k) и y(k), запишем (5.135) в виде

(5.136)

где матрица G₁ имеет размерность r  n, а матрица G₂  размерность r  p.

Вычисляя z-преобразование от обеих частей уравнения (5.136), после упрощений получим

(5.137)

Смысл последнего уравнения состоит в том, что управление u(k) получается в виде комбинации обратной связи по состоянию через постоянные коэффициенты и динамической обратной связи по выходу. Передаточную функцию 1/(z – 1) можно рассматривать как цифровую аппроксимацию операции интегрирования.