3.6. Качество процессов в нелинейных системах автоматического управления
3.6.1. Особенности оценки качества нелинейных систем
Для суждения о качестве нелинейных систем можно использовать те же показатели, что и в случае линейных непрерывных процессов. Правда, анализ качества процессов в нелинейных системах связан со значительно большими трудностями, чем в линейных системах.
Так же как в случае линейных систем, показатели качества можно разделить на прямые и косвенные. Прямые методы основаны на построении исследуемого процесса одним из подходящих для данной системы методом. Косвенные методы оперируют теми или иными косвенными показателями, связанными с характером процессов в системе управления.
3.6.2. Метод припасовывания для построения переходных процессов нелинейных систем
Когда характеристика нелинейного звена может быть аппроксимирована ломаной линией, то такую систему можно рассматривать, как кусочно-линейную. Кусочно-линейную систему можно описать совокупностью линейных дифференциальных уравнений, сменяющих друг друга в точках сопряжения. Переходный процесс выражен на интервалах времени решениями этих дифференциальных уравнений, причем конечные значения предыдущего решения и его производные являются начальными условиями для последующего решения.
Наиболее просто метод применяется к релейным системам. В этих системах включение и выключение реле приводит к появлению в цепях управления импульсов постоянной высоты, переменной длительности и чередующейся полярности. Эта особенность процессов в релейной системе сводится к исследованию поведения линейной части системы при воздействии на нее названных импульсов. Принцип суперпозиции позволяет при этом найти общую реакцию линейной части системы на любое число импульсов путем суммирования реакций системы на каждое воздействие. По мере роста времени число слагаемых увеличивается.
Рассмотрим пример нелинейной системы.
Рис. 3.25. Нелинейная система
Уравнение объекта
(3.126)
и уравнение регулятора
.
(3.127)
Нелинейная часть регулятора представлена на рис. 3.26.
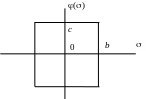
Рис. 3.26. Нелинейная характеристика регулятора
Общее уравнение замкнутой системы:
.
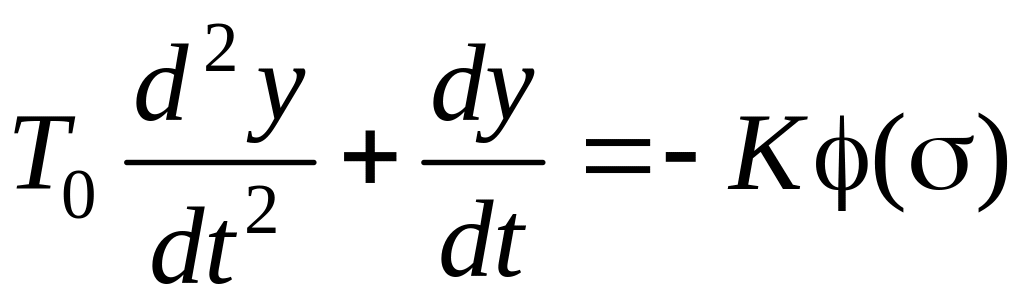(3.128)
Пусть начальное состояние выходной переменной
y(0) = b.
Пусть качественный вид переходного процесса имеет вид, изображенный на рис. 3.27.
()
y
b
b
c
c
D
B
A
t
t
0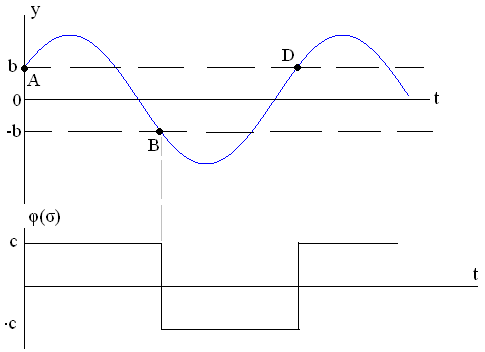
Рис. 3.27. Качественный вид переходного процесса
Можно рассмотреть отдельно участки AB и BD, отсчитывая время на каждом из них от нуля.
На участке AB уравнение системы с учетом отрицательной обратной связи и y = имеет вид
.
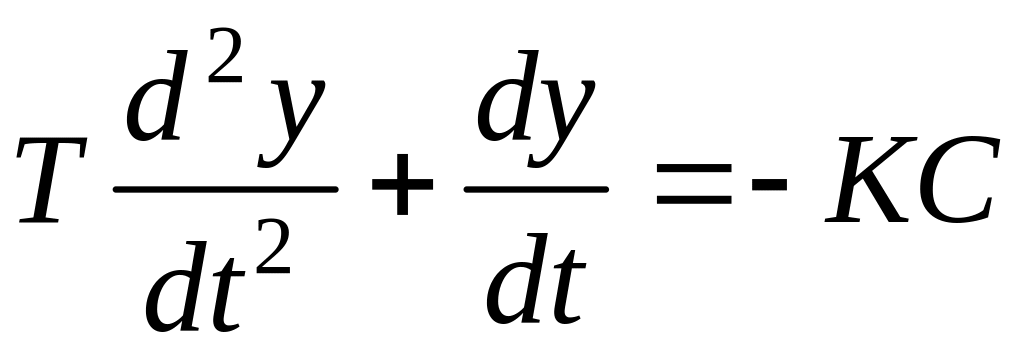(3.129)
Последовательно интегрируя уравнение (3.129), получаем:
;
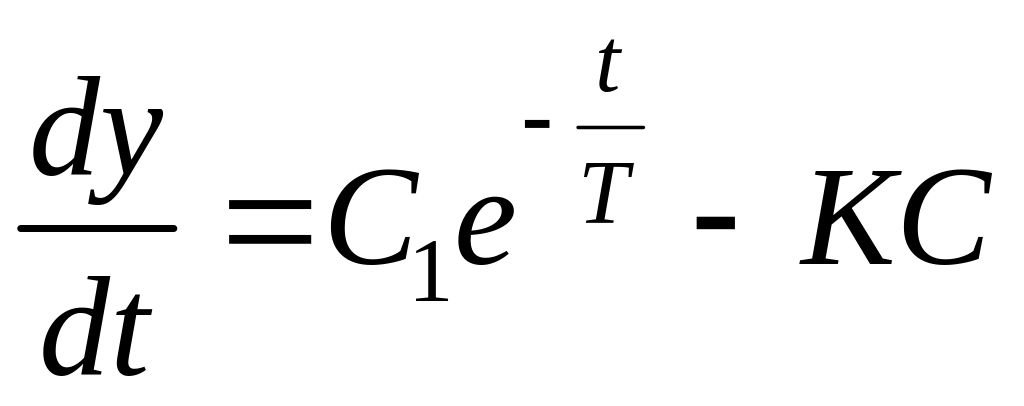(3.130)
.
(3.131)
С учетом начальных условий постоянные интегрирования равны:
.
(3.132)
На участке BD имеем модель системы:
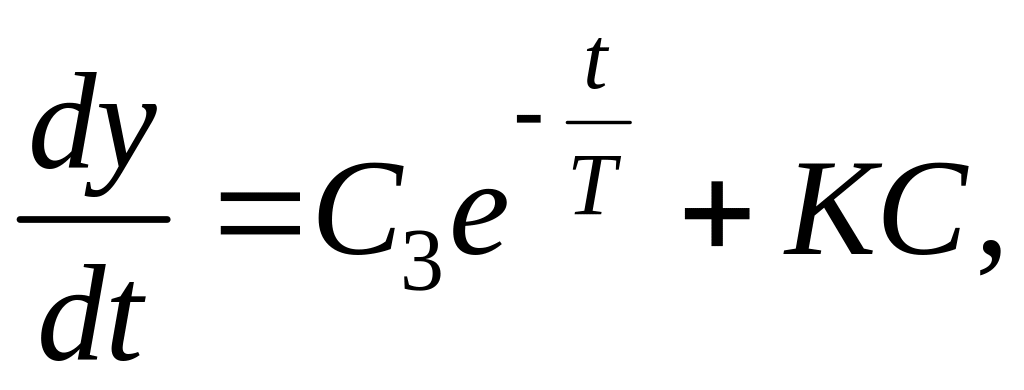
Начальные условия для участка BD можно определить из уравнения (3.130) для предыдущего участка:
(3.133)
где значение
находим из уравнения (3.131):
.
Далее приняв для участка BD начальные условия
получаем
Таким образом, последовательно находят начальные условия для каждого последующего участка переходной характеристики.