3.2.1. Исследование свойств нелинейной системы на основе метода фазовых траекторий. Для нелинейных систем второго порядка
(3.31)
определяются особые точки. Для каждой особой точки выполняется линеаризация нелинейных уравнений. На основе линеаризованных уравнений можно определить корни характеристического уравнения и на их основе выбрать соответствующий фазовый портрет. Сопрягая между собой фазовые портреты в окрестности особых точек, можно оценить свойства нелинейных систем.
Рассмотрим данный метод на основе примера:
dx2/dt = x1 + x2; dx1/dt = 3x2 x1(2 + x12). (3.32)
Найдем особые точки системы
x1 + x2 = 0; –3x2 x1(2 + x12) = 0, (3.33)
откуда получаем решения:
x1 = 0, x2 = 0; x1 = 1, x2 = 1; x1 = 1, x2 = 1. (3.34)
Определим фазовые портреты для каждой пары корней. В окрестности особой точки x1 = 0, x2 = 0 линеаризованные исходные уравнения запишем в виде:
.
(3.35)
Находим характеристическое уравнение:
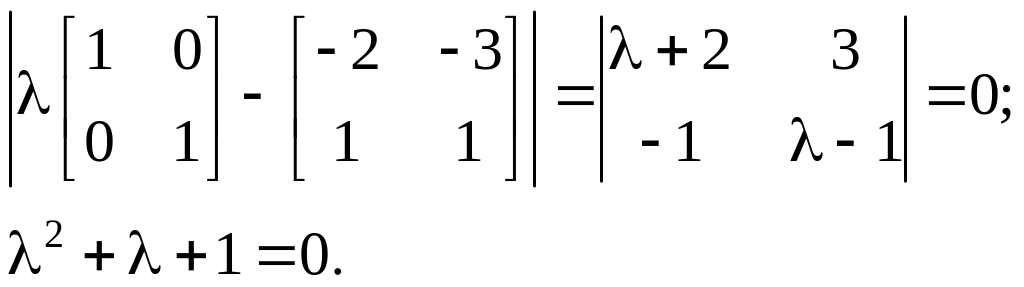(3.36)
Корням
этой
особой точки соответствует устойчивый
фокус.
В окрестности точки x1 = 1, x2 = 1 вводим малые отклонения в координатах:
.
(3.37)
Подставив в исходные уравнения новые переменные и линеаризовав уравнения, получим:
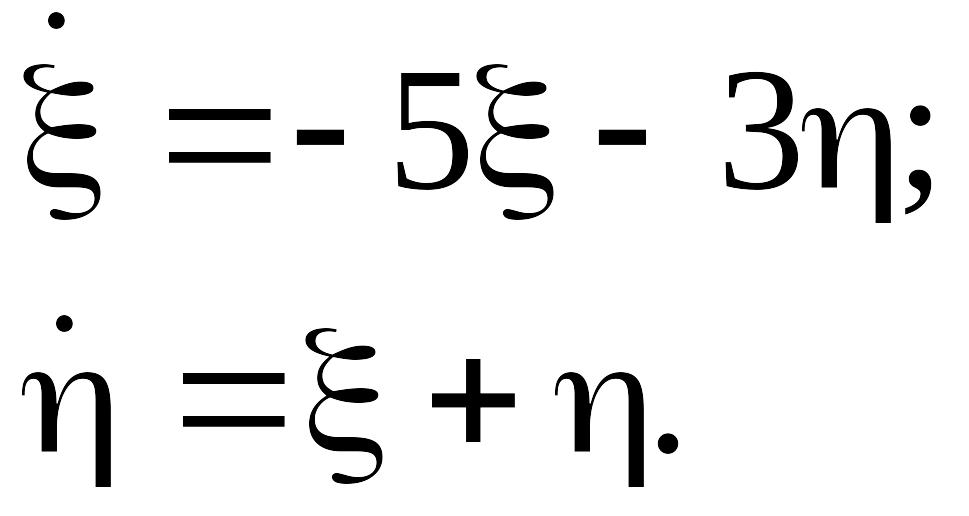
(3.38)
Характеристическое уравнение:
(
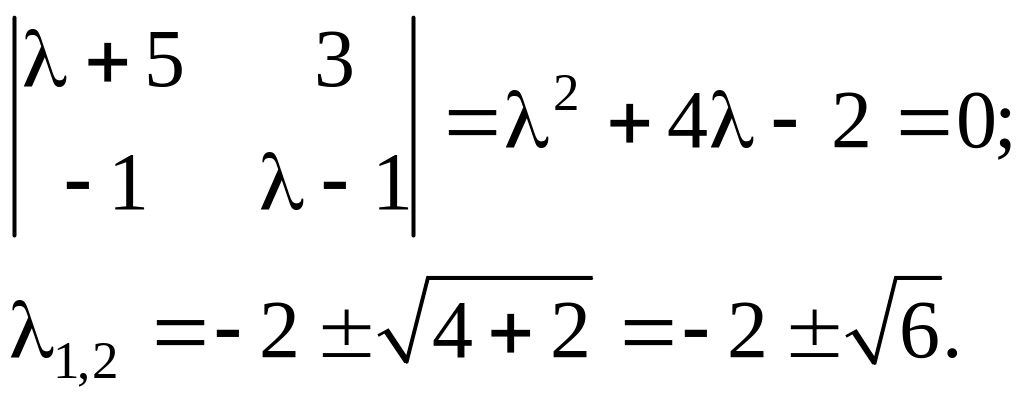3.39)
(3.40)
В окрестности особой точки x1 = 1, x2 = 1 имеем фазовый портрет типа седло.
В окрестности точки x1 = 1, x2 = 1 снова вводим малые отклонения в координатах = x1 + 1, = x2 – 1.
Подставив в исходное уравнение новые переменные и выполнив линеаризацию, получим:
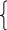
(3.41)
Получим систему уравнений, аналогичную линеаризованным уравнениям для особой точки: x1 = 1, x2 = 1. Тогда имеем фазовый портрет вида седло.
Построим полученные фазовые портреты на плоскости x1, x2, найдя асимптоты траекторий в седловых точках.
Положив = k из уравнения фазовых траекторий
,
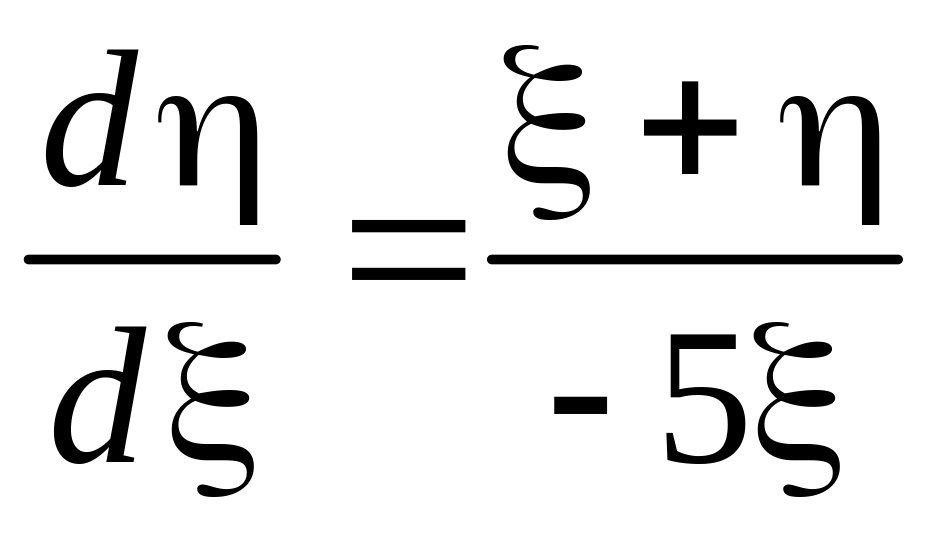(3.42)
получим:
или 3k2
6k
1 = 0.
(3.43)
Откуда находим:
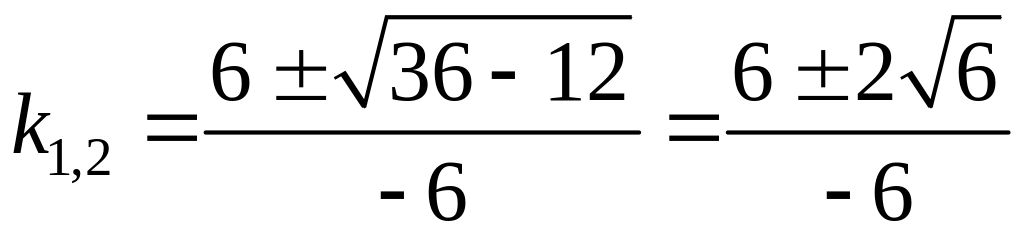(3.44)
Эти асимптоты ( = k) имеют вид отрезков прямых, между которыми существует устойчивый фокус в окрестности начала координат. За пределом малой окрестности вокруг начала координат можно считать состояние системы неустойчивым. Раздел областей устойчивой и неустойчивой работы системы называется предельным циклом.
На основе приведенного примера, показана возможность качественного анализа нелинейных систем по методу фазовой плоскости.
Анализ методом фазовой плоскости и фазового пространства в действительности применим только если заданы:
начальные условия;
скачкообразный входной сигнал;
линейно возрастающий входной сигнал.
Фактически решению поддаются только задачи с начальными условиями, а случаи ступенчатого и линейного входного воздействия приводятся к начальным условиям путем замены переменных.
Фазовый портрет может значительно меняться в зависимости от вида возмущающих функций. Тип нелинейности часто оказывает определенное влияние на особенности поведения нелинейной системы. Для системы с однозначными нелинейностями непрерывного вида можно воспользоваться теоремой: обыкновенное нелинейное дифференциальное уравнение n-го порядка, содержащее любое число однозначных непрерывных нелинейных зависимостей, является моностабильным, если линейное дифференциальное уравнение для приращений переменных в каждой точке фазового пространства является устойчивым.
Термин «моностабильный» означает, что фазовые траектории стремятся к одной или нескольким точкам устойчивого равновесия или уходят в бесконечность. Выражение «линейное дифференциальное уравнение для приращений переменных в каждой точке фазового пространства» связано с кусочно-линейной аппроксимацией однозначной нелинейной зависимости. Наиболее распространенным является насыщение, которое встречается в системах всех порядков и проявляется в разных узлах системы.
Для систем с насыщением, имеющих линейную передаточную функцию с некоторым числом полюсов, но без нулей, насыщение в прямой цепи ослабляет усиление сигнала и приводит к увеличению устойчивости. Если линейная система неустойчива, то единственным эффектом насыщения будет ограничение амплитуды колебаний. Если линейная система устойчива, то система с насыщением также будет устойчива.