
- •Глава 3. Анализ и синтез нелинейных непрерывных систем управления
- •3.1. Особенности нелинейных систем
- •3.2. Фазовое пространство и фазовая плоскость
- •3.2.1. Исследование свойств нелинейной системы на основе метода фазовых траекторий. Для нелинейных систем второго порядка
- •3.3. Устойчивость нелинейных систем
- •3.4. Метод гармонической линеаризации нелинейностей систем автоматического управления
- •3.5. Статистическая линеаризация нелинейных характеристик стохастических систем автоматического управления
- •3.6. Качество процессов в нелинейных системах автоматического управления
- •3.6.1. Особенности оценки качества нелинейных систем
- •3.6.3. Косвенная оценка качества свободных процессов в нелинейных системах
- •3.7. Синтез непрерывных нелинейных систем автоматического управления
- •Контрольные вопросы
Глава 3. Анализ и синтез нелинейных непрерывных систем управления
3.1. Особенности нелинейных систем
Линейные непрерывные системы, которые рассматривались в предыдущих разделах, являются идеализированными моделями фактических систем. Реальные автоматические системы требуют при своем рассмотрении учитывать всякого рода нелинейности. Если система содержит такие нелинейности, пренебрежение которыми может существенно исказить ее качественные свойства, то такая система требует своего математического аппарата, отличного от теории линейных систем. Для элементов, содержащих нелинейности, не выполняется принцип суперпозиции. Это в свою очередь ограничивает возможность применения преобразования Лапласа и Фурье, которые были основой для исследования линейных систем. При изучении нелинейных систем проявляются новые явления, которые не наблюдались в линейных системах. Выявление этих свойств, использование их для улучшения характеристик нелинейных систем, установление характерных особенностей нелинейных систем составляет основу теории нелинейных систем.
Особые свойства нелинейных систем широко используются в технике. На этих свойствах основано генерирование электромагнитных колебаний, выпрямление переменного тока, умножение и деление частот. По динамическим качествам нелинейные автоматические системы во многих случаях превосходят линейные системы.
В общем случае, система автоматического управления называется нелинейной, если хотя бы одно звено системы описывается нелинейным уравнением.
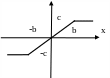
Различают статические и динамические нелинейности. Статические нелинейности характеризуются нелинейными алгебраическими зависимостями. В задачах практики часто удается все нелинейные свойства системы отнести к безинерционным звеньям, что позволяет с достаточной точностью представить систему, состоящей из ряда линейных элементов и элементарных нелинейных безинерционных звеньев, соединенных различными связями. Характеристики некоторых безинерционных нелинейностей приведены на рис. 3.1а, б, в, г, д.
 (3.1)
(3.1)
а)
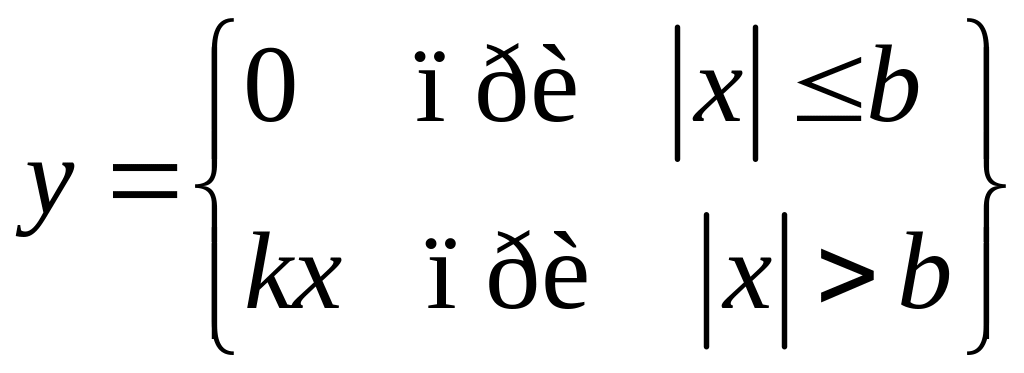 (3.2)
(3.2)
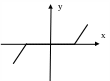
б)
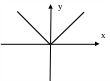
![]() (3.3)
(3.3)
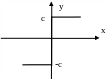
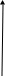
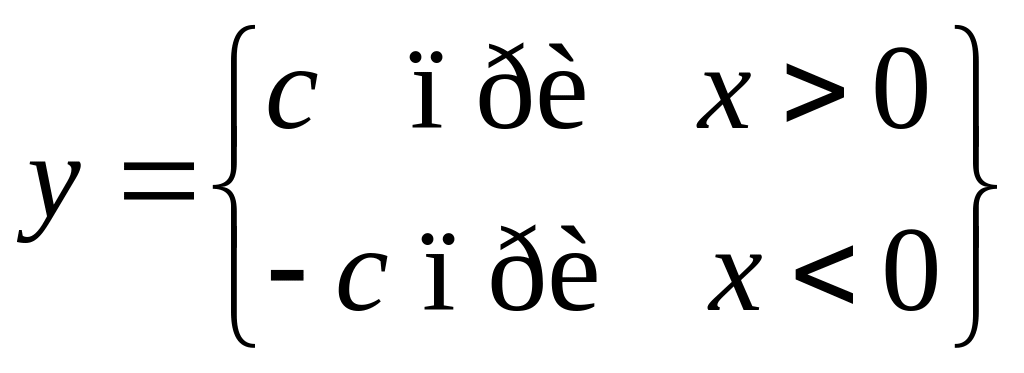 (3.4)
(3.4)
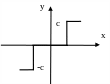
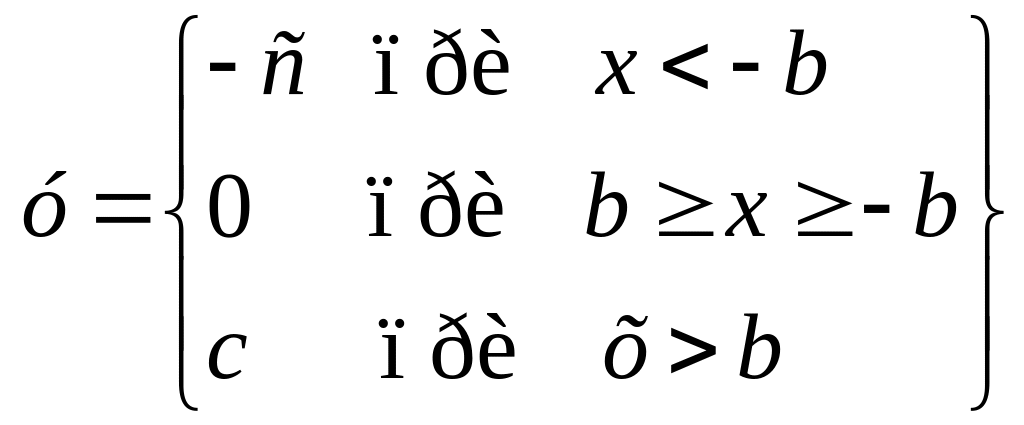 (3.5)
(3.5)
Рис. 3.1. Однозначные статические нелинейности: а – с насыщением; б – с зоной нечувствительности; в – линейные по модулю; г – идеальная релейная;
д - релейная с зоной нечувствительности.
Существуют также петлевые гистерезисные нелинейности (рис. 3.2).
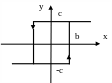
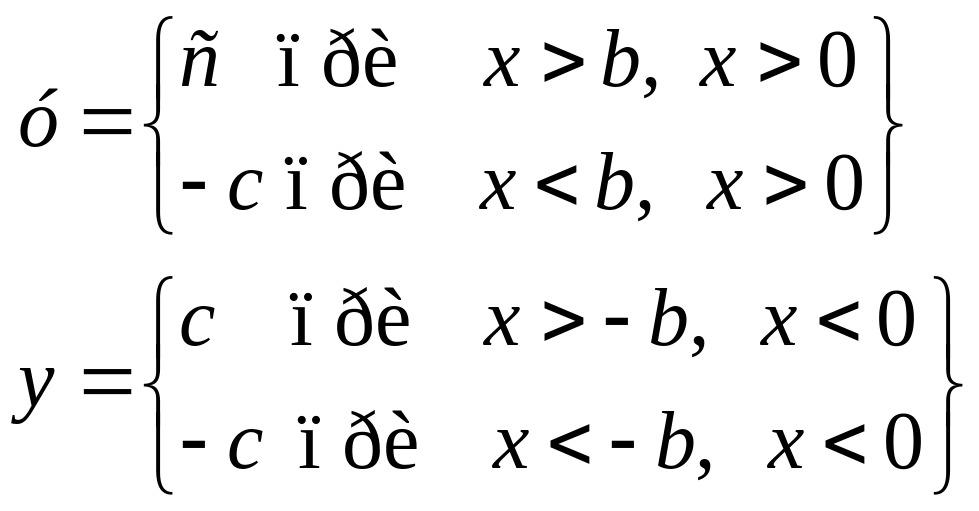 (3.6)
(3.6)
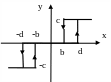
 (3.7)
(3.7)
Рис. 3.2. Петлевые гистерезисные характеристики: а – релейная; б – релейная с зоной нечувствительности.
В отдельных случаях нельзя заменить нелинейности безинерционными звеньями. Например, нелинейная сила вязкого трения характеризуется выражением
![]() .
(3.8)
.
(3.8)
Сила сухого трения в простейшем случае описывается соотношением
![]() при
при
![]() ¹
0; (3.9)
¹
0; (3.9)
С £ F £ C при = 0. (3.10)
Такого типа нелинейности получили название динамических нелинейностей.
3.1.1. Характеристики в статике. Соединение статических нелинейных звеньев
В нелинейных системах преобразование сигнала описывается в общем случае дифференциальным или интегральным нелинейным уравнением и может быть выражено некоторым оператором преобразования Ан. Если входной сигнал x(t), а выходной y(t), то
y(t) = Aн{x(t)}. (3.11)
Как отмечалось ранее, часто преобразование сигнала нелинейным звеном может быть представлено в виде последовательного воздействия линейного оператора W(p), выражающего динамические свойства звена, и нелинейного оператора φ, выражающего статическое преобразование сигнала. Такое представление соответствует эквивалентной схеме, состоящей из последовательного соединения линейного динамического и нелинейного статического звеньев.
В зависимости от последовательности действия линейного и нелинейного операторов получаются различные сигналы преобразования.
При рассмотрении статики нелинейных систем, линейные динамические звенья можно представить в виде limW(p) (при p = 0), что позволяет его объединить с нелинейным статическим звеном. При выводе эквивалентных характеристик нелинейных статических звеньев будем исходить из трех классических видов соединений: последовательного, параллельного и соединения с обратной связью.
Рассмотрим определение характеристики эквивалентного нелинейного элемента на основе отмеченных вариантов соединений двух нелинейных статических звеньев. Пусть имеем последовательное соединение (рис. 3.3).
Можно записать модель эквивалентного звена в виде
![]() . (3.12)
. (3.12)
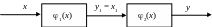
Рис. 3.3. Последовательное соединение нелинейных статических звеньев
Д
1(х)
1(2)
3
х
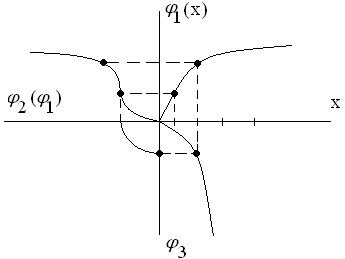
Рис. 3.4. Графическое нахождение характеристики
эквивалентного нелинейного звена
При параллельном соединении двух нелинейных звеньев имеем схему рис. 3.5
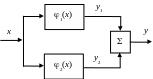
Рис. 3.5. Параллельное соединение двух нелинейных звеньев
![]() .
(3.13)
.
(3.13)
Для построения характеристики эквивалентного нелинейного звена снова используем графический метод (рис. 3.6).
у
у1
у2
у
у1
у2
х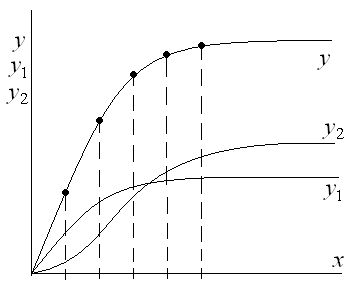
Рис. 3.6. Графическое нахождение характеристики
эквивалентного нелинейного звена
Соединение двух нелинейных звеньев по схеме с обратной связью приведено на рис. 3.7.
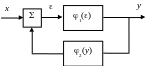
Рис. 3.7. Соединение нелинейных звеньев по схеме с обратной связью
На основании схемы имеем эквивалентную модель
![]() (3.14)
(3.14)
которая не позволяет получить удобную расчетную зависимость.
Можно попробовать получить обратную зависимость:
![]() .
(3.15)
.
(3.15)
Применительно к структурной схеме (рис. 3.7) запишем
![]() ,
(3.16)
,
(3.16)
где знак плюс соответствует отрицательной обратной связи.
Рассмотрим графическое решение для нахождения эквивалентной зависимости. Пусть нелинейные характеристики исходных звеньев имеют вид, представленный на рис. 3.8.
1(x)
2(y)
x
y
a
б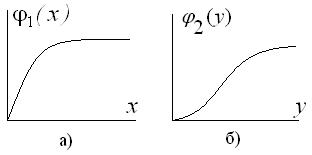
Рис. 3.8. Характеристики нелинейных звеньев.
Преобразованная характеристика первого звена показана на рис. 3.9.
y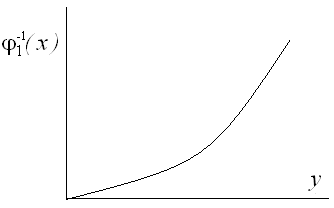
![]()
Рис. 3.9. Обратная характеристика первого нелинейного звена
Просуммировав ординаты характеристик, приведенных на рис. 3.8 и 3.9 получим зависимость, изображенную на рис. 3.10.
y
х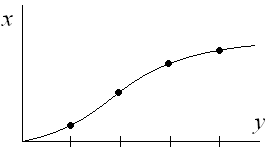
Рис. 3.10. Обобщенная обратная характеристика нелинейной системы
Аппроксимируя значения графика (рис. 3.10) можно получить эквивалентную характеристику нелинейных звеньев:
![]() .
(3.17)
.
(3.17)
