2.14. Синтез инвариантных систем

На работу всех систем автоматического управления оказывают влияние непрерывно меняющиеся внешние условия, параметры самой системы и другие факторы.

Относительно этих факторов в зависимости от рассматриваемой задачи делают различные предположения. Предположим, что каждый из непрерывно меняющихся факторов может быть представлен в виде произвольно меняющейся функции из некоторого класса допустимых функций; причем функции, входящие в этот класс, обладают одними и теми же свойствами. Очень часто их предполагают непрерывными и дифференцируемыми.

Если по условию задачи требуется, чтобы одна или несколько переменных системы не зависели от некоторого воздействия (внешнего или внутреннего), которое представляется функцией из класса допустимых воздействий, то в этом случае говорят об инвариантности выбранной переменной относительно указанного воздействия. Пусть работу системы управления описывают системой дифференциальных уравнений вида:

= f_i (t, x₁,…, x_n, v, v^’,…,vⁿ);

i =1, n,

где x₁, …, x_n – обобщенные координаты системы управления; v(t), …, vⁿ – произвольное воздействие.

Проблему инвариантности координаты х, относительно воздействия v можно сформулировать как задачу отыскания условий на функции f_i, при выполнении которых значения координаты х не зависят от v.

Нередки случаи, когда на систему автоматического управления действуют не одна, а несколько возмущающих воздействий и ставится задача независимости каких-то координат от всех этих возмущений. Такие задачи называют задачами инвариантности.

Возникновения идей инвариантности связано с работами Г. В. Щипанова, который в 1939 г. сформулировал «условия компенсации» возмущений.

Пример структурного анализа влияния возмущения на одну из координат. Пусть система описывается системой уравнений

a₁₁x₁ + a₁₂x₂ = v(t);

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = 0;

a₃₂x₂ + a₃₃x₃ = 0.

На основании приведенных уравнений можно составить структурную схему, позволяющую находить переменные х (рис. 2.15)

v(t)

x₁

1/a₁₁

x₃

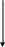
a₁₃

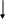
a₂₁

a₂₃

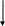
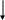
1/a₂₂

x₂

a₃₂

1/a₃₃

x₃

Рис. 2.15 Структурная схема системы

Из данной структурной схемы видно, что возмущение напрямую влияет на координату х₁. При такой структуре системы практически невозможно обеспечить инвариантность координаты х₁. Попробуем изменить порядок исходных уравнений:

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = 0;

a₃₂x₂ + a₃₃x₃ = 0;

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = v(t).

И составим новую структурную схему

x₂

a₂₂

1/a₂₂

x₁

x₃

a₂₃

a₂₃

1/a₂₂

v

1/a₁₃

a₁₁

a₃₃

a₁₂

Рис. 2.16. Преобразованная структурная схема системы

Вторая структурная схема имеет два канала для воздействий от возмущения v к переменной х₁. Наличие двух каналов позволяет организовать прохождение возмущения таким образом, чтобы суммарный эффект от возмущения сводился к нулю. Поэтому можно считать, что для обеспечения инвариантности координаты х относительно возмущения v, необходимо обеспечить прохождение возмущения к координате х, как минимум, по двум координатам.

Это условие было названо Б. Н. Петровым «принципом двухканальности».

Рассмотрим использование данного принципа для одноконтурной системы рис. 2.17.

В данной системе возмущение v доступно измерению, что позволяет искусственно создать второй канал для прохождения возмущения на выход системы.

W_v

v

g

W_p(p)

Y

W_об(p)

W_p(p)

u

Рис. 2.17. Одноконтурная система управления

Новую систему можно представить в виде рис. 2.18.

W_k(p)

v



W_p(p)

g

u

Y

W_об(p)

W_v(p)

Рис. 2.18. Структурная схема системы с компенсатором W_k(p)

На основании структурной схемы (рис. 2.18) можно записать условие компенсации возмущения v:

vW_k(p)W_p(p) = vW_v(p). (2.116)

Откуда имеем

W_k(p) = W_v(p)/W_p(p). (2.117)

При условии физической реализуемости выражения (2.117) система обеспечивает полную инвариантность выходного сигнала y от возмущения v. Системы управления такого типа получили наименование комбинированных, поскольку эти системы реализуют как принцип управления, основанный на обратной связи, так и принцип управления по возмущению.

Синтез систем с комбинированным управлением осуществляется в два этапа. На первом этапе принимается равным нулю возмущение v и осуществляется синтез регулятора W_p(p) на основе одного из рассмотренных методов. После определения структуры и параметров W_p(p) переходят ко второму этапу синтеза системы – расчету W_k(p) на основании (2. ). Если расчетная функция W_k(p) физически не реализуется, то необходимо разложить ее в ряд:

W_k(p) = C₀ + C₁p + C₂p² +… (2.118)

и ограничиться приведенными тремя составляющими. В этом случае система будет иметь лишь частичную инвариантность.