2.13. Системы с модифицированным упредителем Смита и компенсацией кратного высшего возмущения

САР с линейным упредителем Смита, подверженная неизмеряемым возмущениям f₁(t), может работать неудовлетворительно, если передаточная функция объекта (рис. 2.9, 2.12) по каналу управляющего воздействия имеет полюса около начала ординат.

Для получения желаемых переходных процессов и нулевой статической ошибки при действии неизмеряемых возмущений f₁(t) предложена модификация алгоритма Смита с прогнозом для управления многомерными системами с запаздыванием (рис. 2.13: М(p)  динамический компенсатор, ).

В этом случае передаточная функция между внутренним возмущением f₁(t) и выходом у(t) определяется выражением

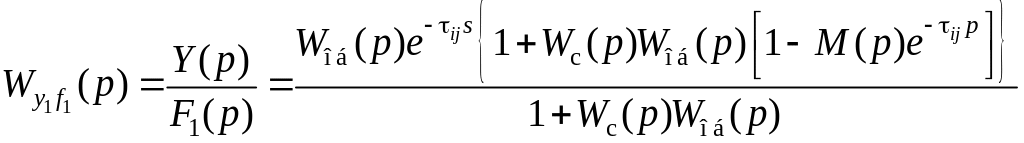
Если при этом передаточная функция регулятора W_с(p) имеет интегратор, полюса М(p) могут иметь произвольные заранее выбранные значения

для – ₁ любых полюсов W_об(p);

,

то можно получить желаемые переходные процессы в системе при следующих условиях:

1) уравнение состояния объекта

, .

, u,

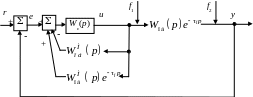
Рис. 2.12. Структурная схема САР с алгоритмом Смита

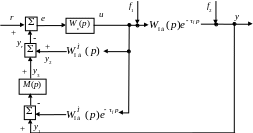
Рис. 2.13. Структурная схема модификации алгоритма Смита с прогнозом

;

;

;

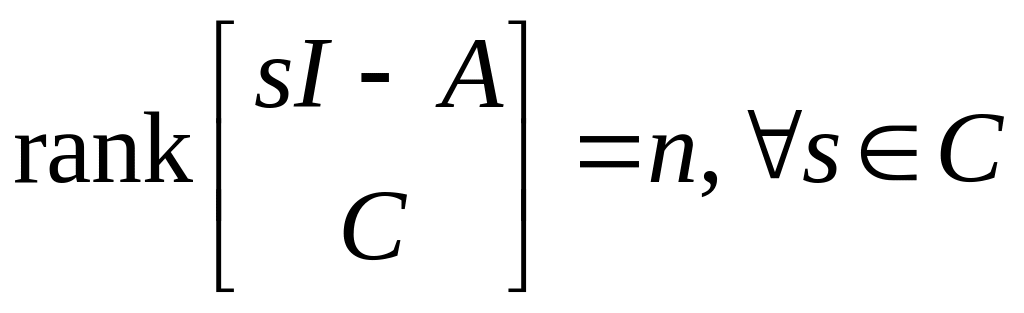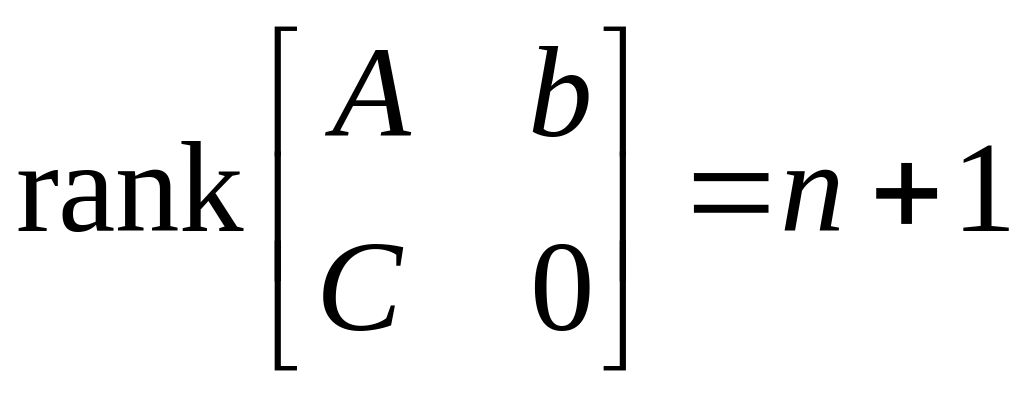2) уравнение состояния регулятора

, , .

3) динамическому компенсатору соответствует:

; , ,

где , , , ,

Вместе с тем получить желаемую реакцию системы на возмущение f₁(t) можно путем переноса точки включения стабилизирующего устройства на выход опережающего участка объекта регулирования и замены передаточной функции объекта W_об(p), используемой в упредителе Смита в качестве внутренней отрицательной обратной связи, на коэффициент усиления объекта k_ин. Однако это снижает быстродействие системы при отработке задания.

Для восстановления быстродействия системы по заданию и получения желаемых переходных процессов на возмущения f₁(t) и f₂(t) рассмотрим усовершенствованный вариант модификации алгоритма Смита с прогнозом для управления многомерными системами с запаздываниями и неизмеряемыми ступенчатыми возмущениями, реализованный в схеме, изображенной на рис. 2.14, где W_об(p) = = W_оп(p)W_ин(p), т. е. в объекте выделены опережающий и инерционный участки: W_c(p)= W_p(p).

Здесь передаточная матрица инерционного участка объекта обозначается в виде:

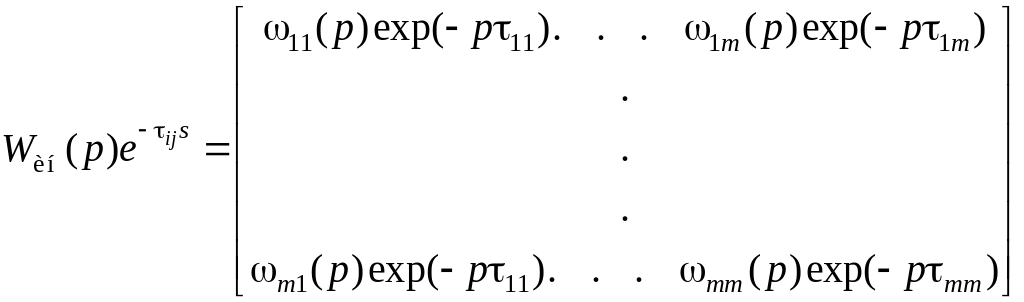
где _ij(p)exp(p_ij)  передаточная функция между j-м входом и i-м выходом;

модель инерционного участка без запаздываний определяется матрицей

,

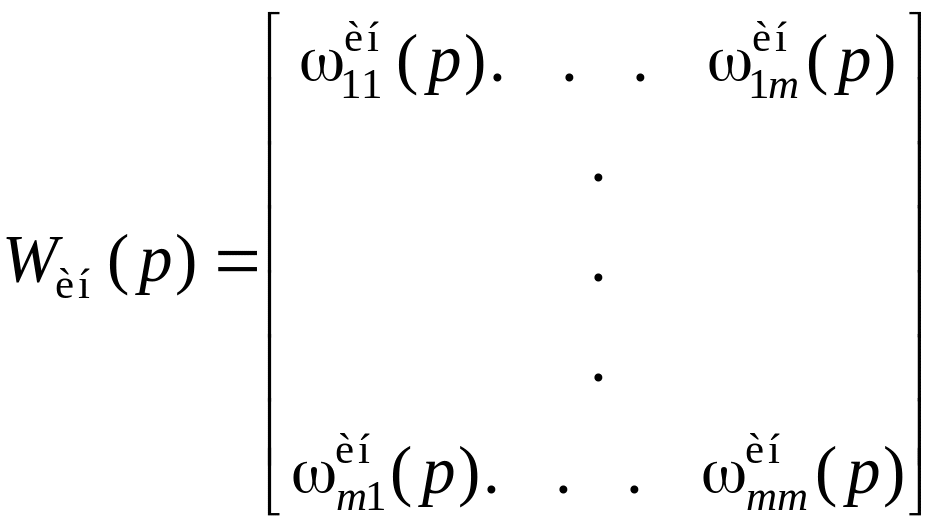а матрица модели опережающего участка имеет вид

.

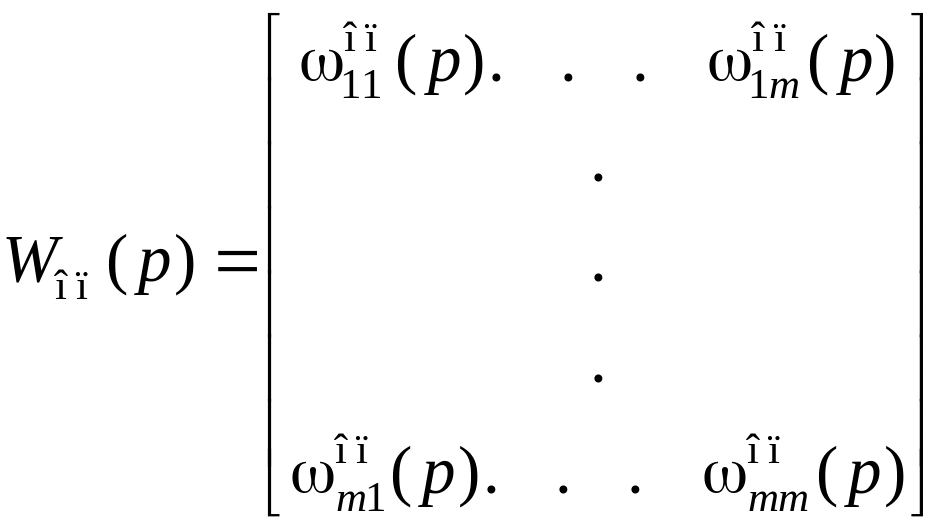При этом выход Y(p) связан с возмущением F₂(p) выражением

,

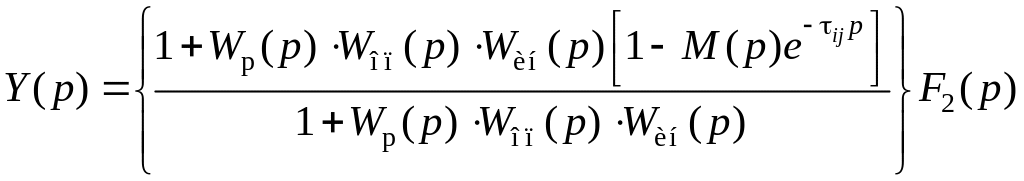где M(p) = 1 + W_kf2(p).

Здесь матрица компенсатора внешнего возмущения F₂(p) имеет вид

,

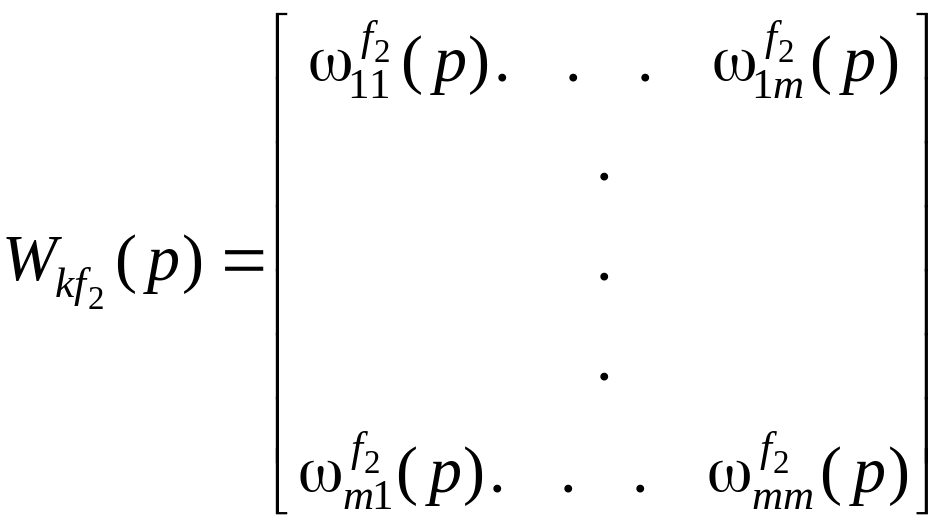а матрица корректора задания равна

.

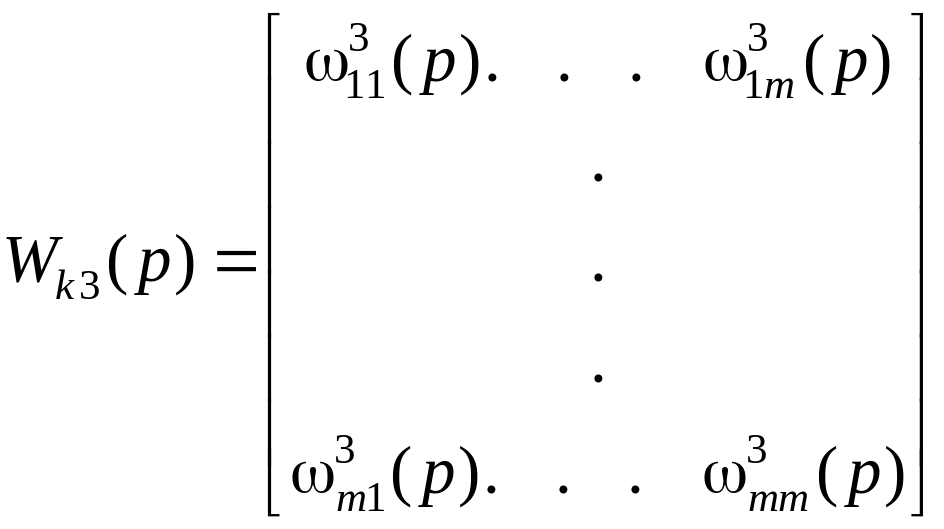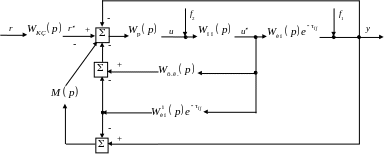
Рис. 2.14. Структурная схема усовершенствованной модификации алгоритма Смита с прогнозом

За условие автономности принимаем условие диагональности матрицы [I + W_р(p)W_ин(p)W_оп(p)], обращение в нуль внедиагональных элементов которой устраняет влияние связей между подсистемами. В скалярной форме условия равенства нулю внедиагональных элементов имеют вид:

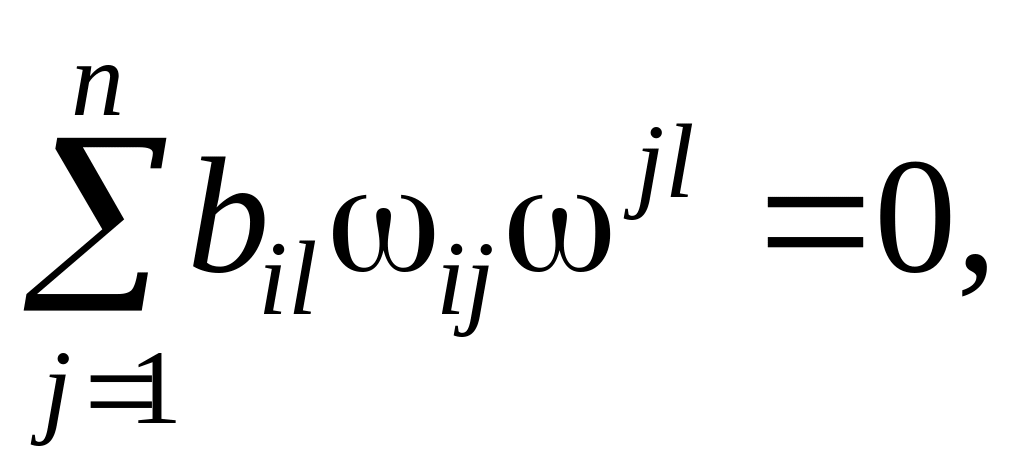i, ,

где

Обозначив через алгебраическое дополнение элемента

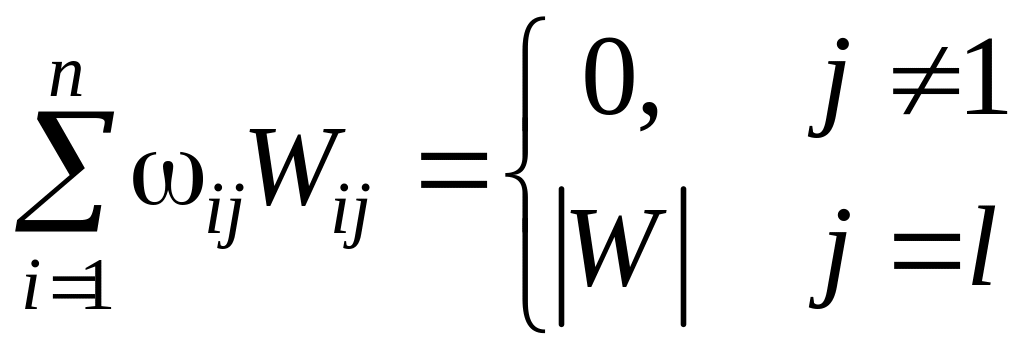
определителя |W|, с учетом известного соотношения при I = l получим /5/:

.

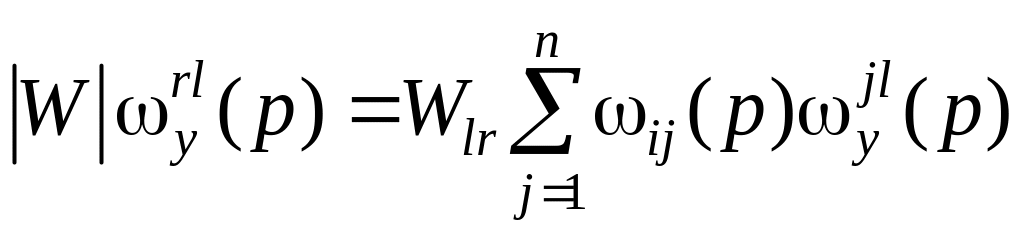В частности при r = l имеем

.

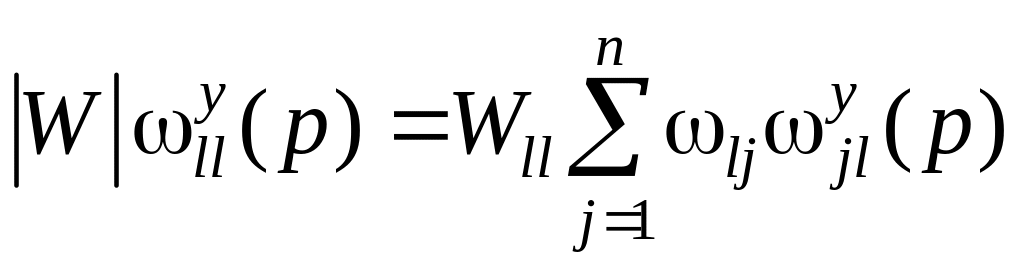Отсюда окончательно получаем выражение внедиагональных элементов матрицы условного регулятора W_y(p) = W_p(p)W_оп(p) через диагональные элементы

.

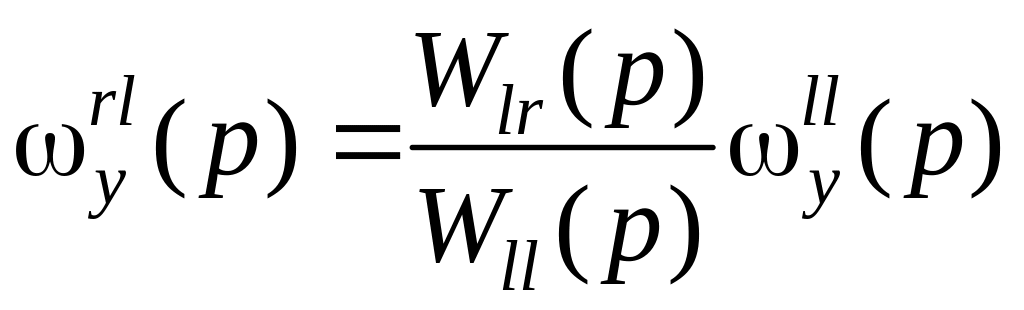Так как выбор диагональных элементов матрицы регулятора при этом произволен, имеется возможность обеспечить помимо автономности ряд других условий. Если при этом М(p) имеет заданные полюса в левой полуплоскости, а регулятор содержит в алгоритме регулирования интегратор, то связь выхода системы с возмущением f₂ определяется только корнями

и полюсами M(p). Это позволяет получить желаемые переходные характеристики в системе при основных возмущениях.

Пусть уравнение состояния модели инерционного участка имеет вид

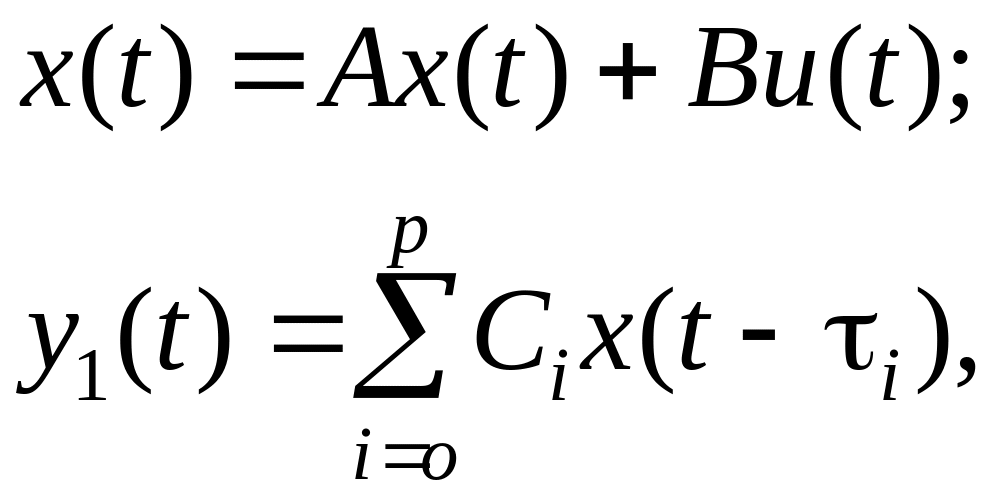
где p  целое положительное число;

x  (n  l)-мерная переменная состояния;

u  (m  1)-мерный вход;

y₁  m  1  мерный выход;

A, B и C_i  постоянные матрицы соответствующих размерностей;

_i  запаздывания, соответствующие условию 0 = ₀ < ₁ < … < _p.

При этом: система (А, В)  управляема;

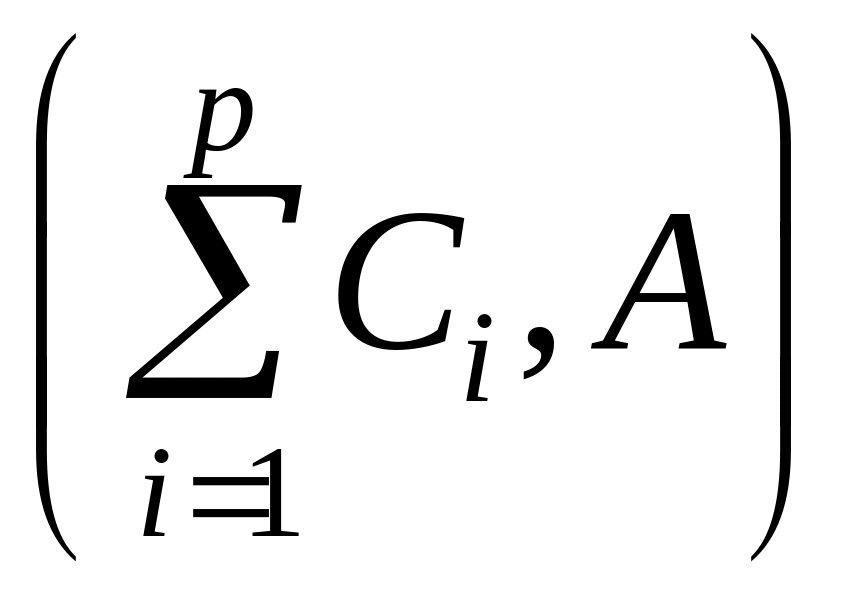– наблюдаема;

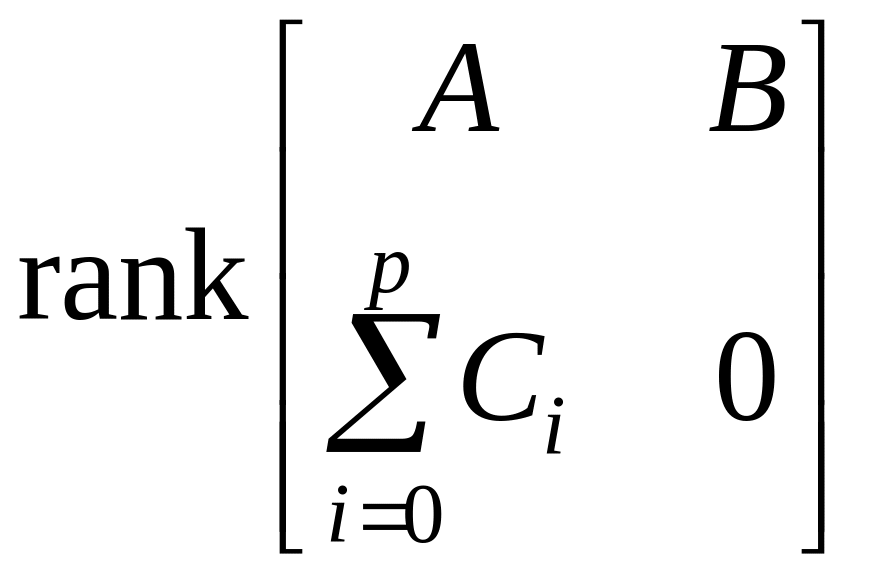
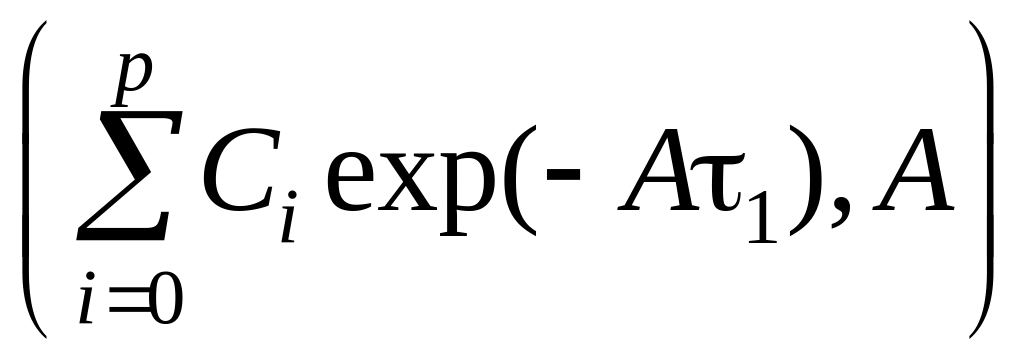– наблюдаема;

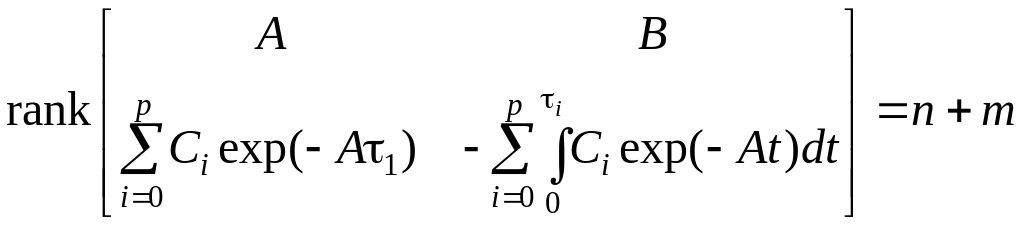
Если W_ин(p) соответствует:

; ,

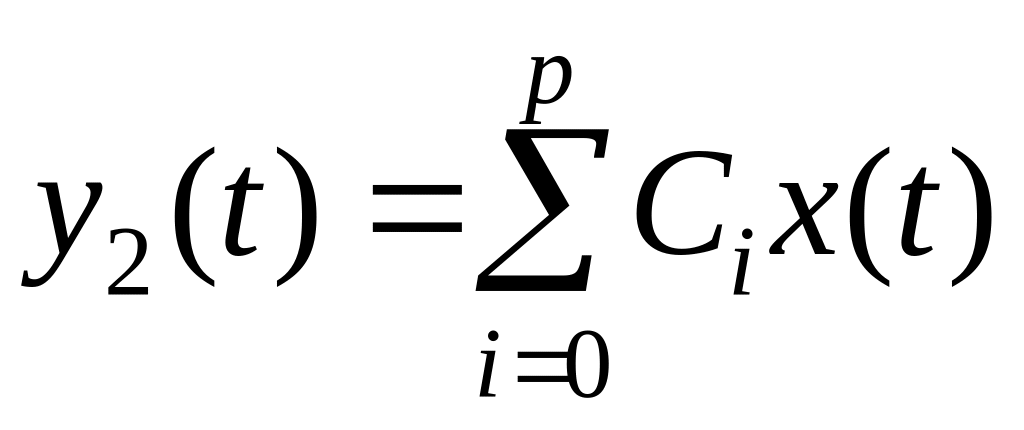а вектор компенсатора М(p) представить в виде

где , , , , то динамический компенсатор, устраняющий влияние возмущений, будет соответствовать уравнению .

Вместе с тем следует отметить, что реализация компенсатора полной автономности и инвариантности по f₂ оказывается чаще всего нереализуемой. В связи с этим представляют интерес методы, позволяющие получить частичную автономность и инвариантность, при которых желаемые показатели качества достигаются приближенно.