2.9. Синтез систем автоматического управления объектами с доминирующей величиной запаздывания

2.9.1. Системы с упредителем Смита. Если объект управления содержит запаздывание большой величины и отсутствует возможность разделения объекта на отдельные составляющие, то в этом случае предлагается специальная структура систем, например, с использованием упредителя Смита (рис. 2.8).

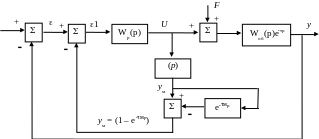
Рис. 2.8. Структурная схема системы с упредителем Смита

Система содержит искусственно созданные элементы модели объекта W_oб^м(p), e^-τмp Принимаем, что

W_oб^м(p) = W_oб(p) и τ_м = τ. (2.68)

За счет внутреннего искусственного контура достигается «предсказание» будущего поведения системы, что и определяет термин «упредитель Смита».

Оценим влияние упредителя на характеристики системы без конкретизации структуры регулятора W_p(р).

На основе схемы можно записать систему уравнений:

ε = g  y;

ε₁ = ε  y_м ;

u = W_pε; (2.69) y_м = ;

y = W_oбe^-τp(u + F).

Исключая промежуточные переменные, получим:

Y(р) = +

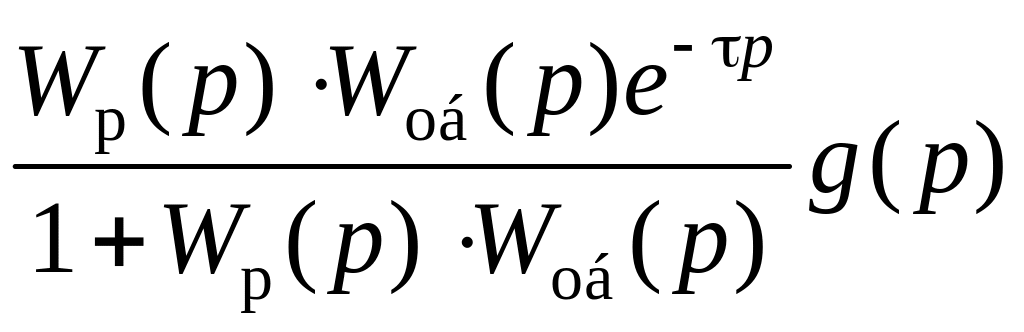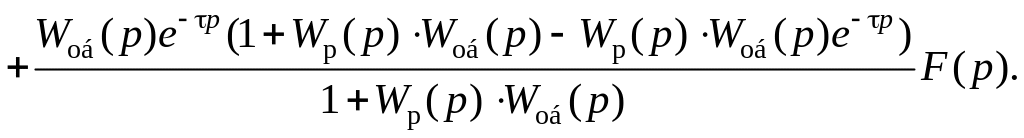(2.70)

Если система работает в диапазоне частот, где

,

то уравнение (2.70) можно приближенно записать

. (2.71)

Из уравнения (2.71) можно записать, что выходной сигнал формируется за минимальное время, определяемое физическими ограничениями объекта, связанными с e^p.

Выбор структуры и расчет параметров настройки регулятора можно выполнить на основе расчетной части системы, выделенной из рис. 2.9

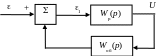
Рис. 2.9. Расчетная часть системы с упредителем Смита

Для данной схемы можно использовать П-, ПИ- или ПИД-регулятор в зависимости от требования к точности работы системы и условия:

. (2.72)

2.10. Синтез систем управления многомерными объектами

Многомерный объект управления (рис. 2.10) содержит m управляющих каналов и n выходов.

u₁

Y₁

W_об(p)

u_m

Y_n

Рис. 2.10. Многомерный объект управления

В отличие от одноканальных систем, многомерным системам присуще такое свойство, как взаимосвязанность каналов. Учет взаимосвязанности каналов является одним из важнейших требований при синтезе систем управления такими объектами. Для этого воспользуемся методом Бристоля, который заключается в построении специальной матрицы

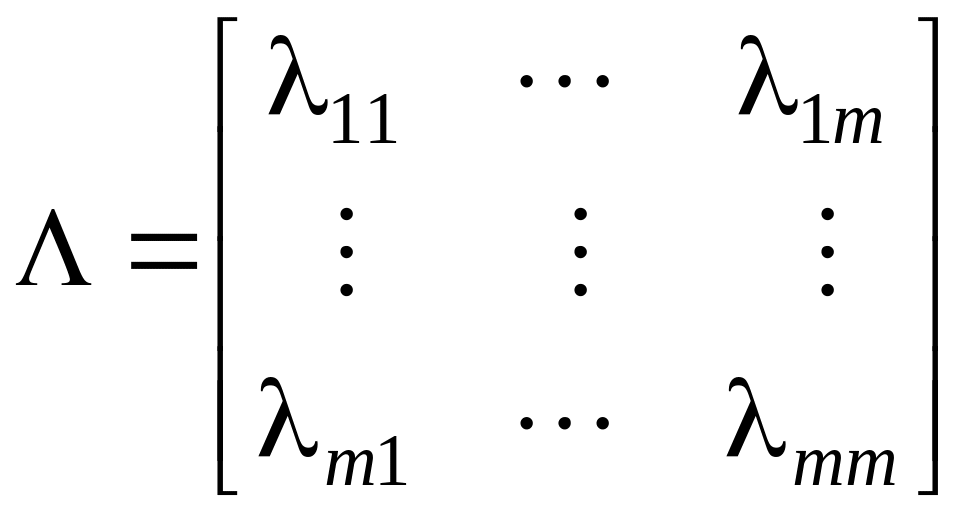, (2.73)

элементы которой в статике соответствуют соотношению _{I j} = = (dy_i/du_j)/(dy_i/du_j) (все контуры разомкнуты/все контуры, кроме u_с, замкнуты), где y_i – установившееся значение i-го выхода; u_j – управление.

Необходимо определить коэффициенты передаточной матрицы

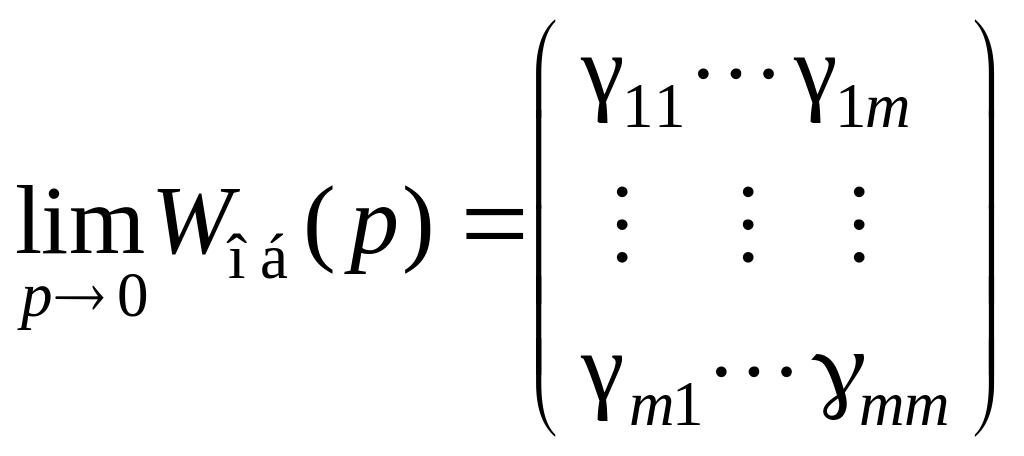. (2.74)

Затем нужно найти элементы матрицы

[W₀^T(0)]^1. (2.75)

Элементы матрицы  находятся из выражения

_ij = [W(0)]_ij[W^T(0)]_ij^1 (2.76)

путем перемножения элементов с одинаковыми индексами.

Анализ матрицы  показывает, что система имеет слабую связанность, если диагональные элементы близки к единице, а недиагональные существенно меньше (близки к нулю).

Один из первых методов синтеза систем был основан на компенсации или развязывании перекрестных связей объекта и получил название автономного регулирования.

Автономное регулирование обеспечивает раздельное управление выходами объекта за счет включения в состав системы компенсатора, например, между регулятором и объектом. Будем рассматривать последовательную цепь из компенсатора и объекта, как новый расширенный объект. Можно потребовать, чтобы каналы расширенного объекта были не связаны между собой.

Передаточная матрица расширенного объекта равна

W_об(p)  W_k(p) = (р), (2.77)

где W_k(p), (p) – передаточные матрицы соответственно компенсатора и расширенного объекта.

В качестве элементов передаточной матрицы расширенного объекта принимаются диагональные элементы передаточной матрицы исходного объекта:

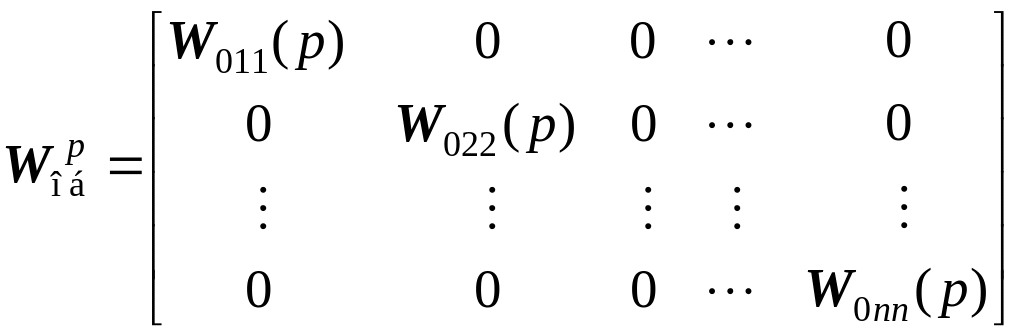(2.78)

или в виде

(p) = diagW_oб(p). (2.79)

Тогда можно найти передаточную матрицу компенсатора

W_k(p) = (p)diagW_об(p). (2.80)

Полученные математическим путем результаты требуют их оценки из условий физической реализуемости.

При невозможности полной реализации компенсатора ограничиваются частично реализуемым компенсатором на основе использования ограниченного числа членов разложения передаточных функций в ряд.