2.7. Синтез систем управления с апериодической реакцией (минимальным перерегулированием) и желаемым временем переходного процесса

К системам с апериодической реакцией относятся такие, у которых перерегулирование находится в диапазоне 0,12%, установившаяся ошибка равна нулю и высокое быстродействие. Рассмотренный метод применим для синтеза систем управления, имеющих замкнутую передаточную функцию вида

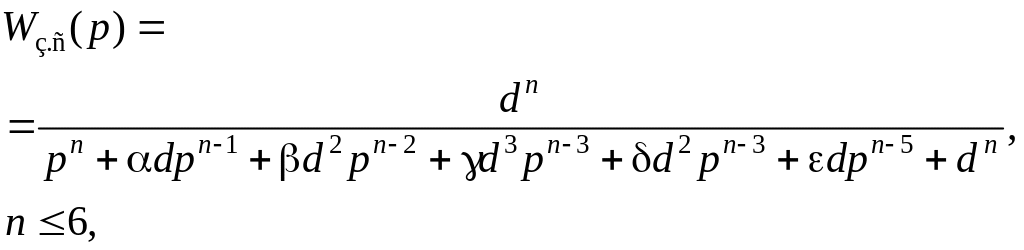(2.36)

где d, α, β, γ, δ, ε  коэффициенты.

Выражение (2.36) можно нормировать, введя обозначение и записать

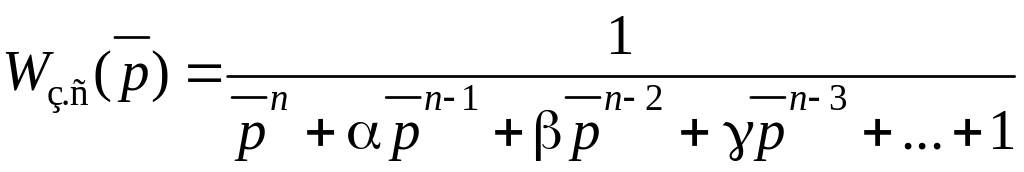. (2.37)

Нормированное время переходного процесса определяется по соотношению

, (2.38)

где t_р.ж  желаемое время переходного процесса системы.

Коэффициенты и характеристики переходного процесса нормированной системы с апериодической реакцией приведены в табл. 2.2.

Таблица 2.2

Коэффициенты и параметры переходной характеристики системы

Порядок системы	Коэффициенты знаменателя передаточной функции системы					Перерегули-рование, %	Нормированное время переходного процесса
	α	β	γ	δ	ε
2	1,82					0,10	4,82
3	1,90	2,20				1,65	4,04
4	2,20	3,50	2,80			0,89	4,81
5	2,70	4,90	5,40	3,40		1,29	5,43
6	3,15	6,50	8,70	7,55	4,05	1,63	6,04

При условии, что замкнутая система состоит из регулятора и объекта управления с единичной отрицательной обратной связью по выходу, записывается передаточная функция регулятора

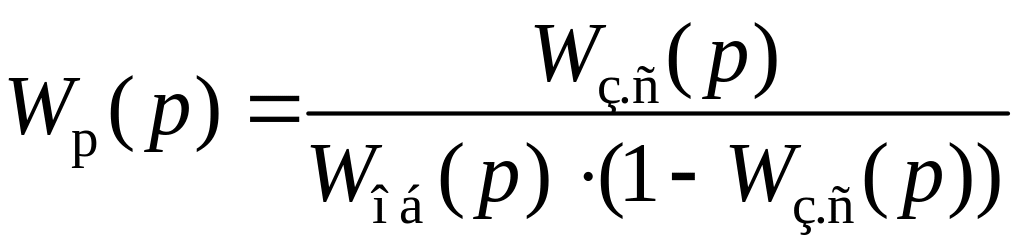. (2.39)

Размерность передаточной функции W_з.с выбирается равной или большей размерности передаточной функции объекта, что позволит обеспечить физическую реализуемость регулятора. Зная порядок системы и желаемое время переходного процесса, можно на основе таблицы определить модель W_з.с (p).

В качестве примера рассмотрим синтез системы управления, которая обеспечивала бы t_р.ж = 120 с с объектом управления вида

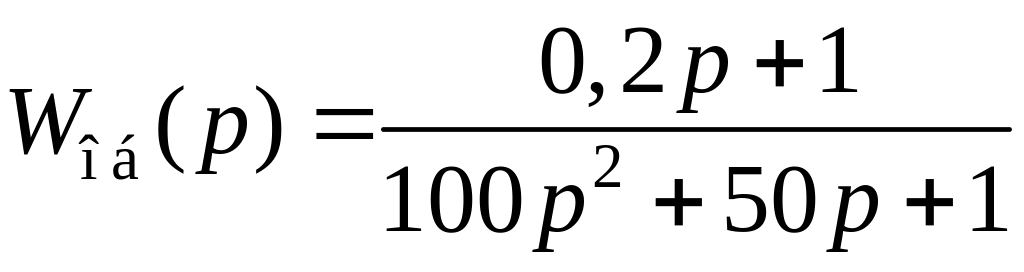. (2.40)

Выберем порядок системы равным порядку объекта, т. е. n = 2.

На основании табл. 2.2 и формул (2.38) находим коэффициенты для передаточной функции замкнутой системы

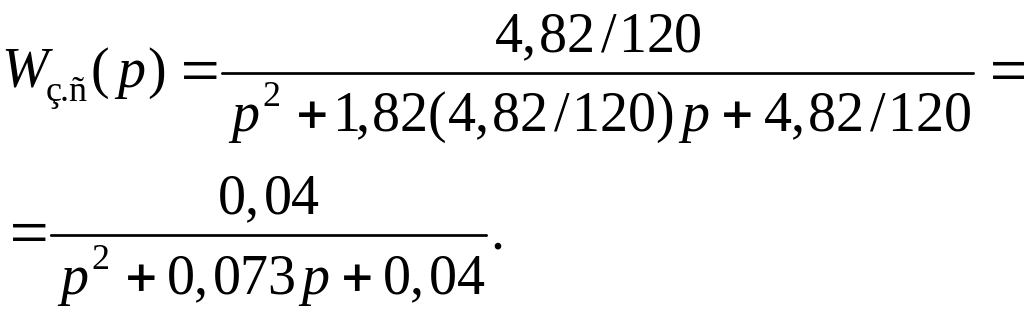. (2.41)

Передаточная функция регулятора, согласно (2.39), равна

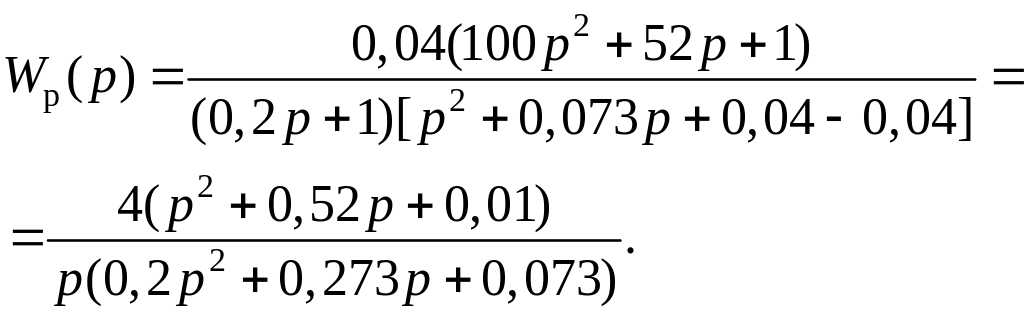(2.42)

Если разложить данное выражение в ряд и ограничиться положительными составляющими, то получим W_p(p) ≈ 12,74 + 0,548∙1/p + + 5,62p, которая соответствует типовому ПИД-регулятору.

2.8. Синтез двухконтурных систем автоматического регулирования

2.8.1. Синтез каскадных систем автоматического регулирования. Для объектов данного класса характерна возможность декомпозиции объекта на два последовательных звена с измерением сигналов после каждого звена. Наиболее эффективна работа таких систем, когда инерционность первого звена объекта хотя бы на порядок была меньше инерционности второго звена.

Структура двухконтурной системы такого класса приведена на рис. 2.2.

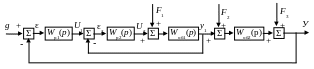
Рис. 2.2. Структура каскадной системы управления

Обычно вторичный регулятор W_p2(p) является пропорциональным. Он улучшает характеристики части объекта W_об1(p), которая обычно не содержит запаздывания.

Внутренний контур можно рассчитывать как одноконтурную систему, исходя из требований высокого быстродействия, например, исходя из желаемого времени переходного процесса по координате y₁. Затем внутренний контур сворачивается до эквивалентного звена, которое присоединяется последовательно к W_об2(p)e^p.

Далее, с учётом технологических требований к системе, выбираем один из рассмотренных ранее методов синтеза.

2.8.2. Синтез систем автоматического регулирования с дифференцированием промежуточного сигнала. Широкое распространение в теплоэнергетике получили также каскадные системы автоматического регулирования (КСАР).

Произведем декомпозицию двухконтурной системы автоматического регулирования на две одноконтурные и рассмотрим внутренний быстродействующий контур со стабилизирующим регулятором. Структура и параметры динамической настройки последнего можно определить в зависимости от выбранного критерия качества и вида возмущения любым из известных способов по передаточной функции опережающего участка.

Пусть расчетная модель опережающего участка в относительных единицах имеет вид

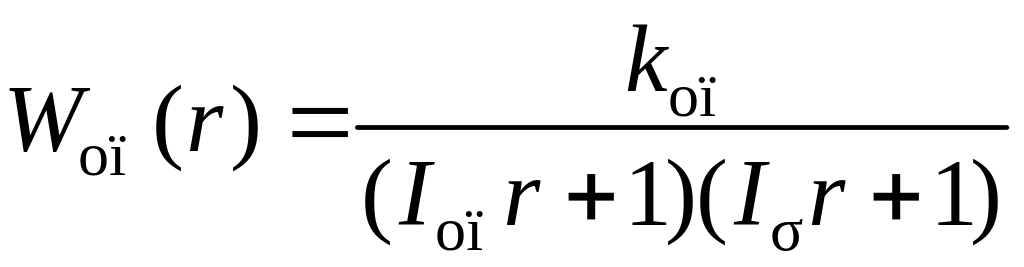, (2.42)

где ; ; .

Обозначив через – заданное относительное время разгона экстремали оптимального переходного процесса по промежуточной регулируемой величине у₁(t), найдем оптимальную структуру и динамические настройки стабилизирующего регулятора W_p1(r). В соответствии с данными табл. 2.3 оптимальным регулятором будет ПИД-алгоритм регулирования, параметры динамической настройки которого можно определить по следующим соотношениям:

(2.43)

где K_р1 – относительный коэффициент усиления регулятора; I_u1I_1 – соответственно относительные постоянные времени интегрирования и дифференцирования ПИД-регулятора.

Покажем, что в частном случае при замене ПИД-регулятора ПИ-алгоритмом регулирования, параметры динамической настройки которого определяют по формулам (2.18) при I_1 = 0 и выборе T_зд1 = 2, качество регулирования в системе по задающему воздействию будет определяться передаточной функцией

,

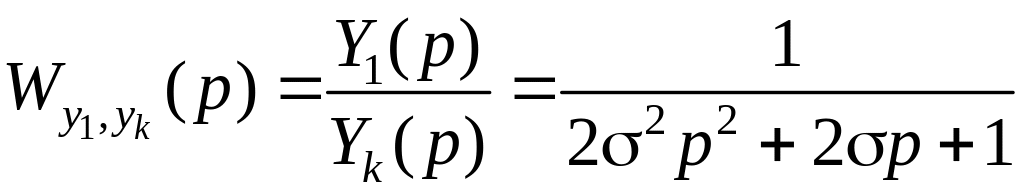которому соответствуют следующие прямые показатели оптимального переходного процесса

 = 4,3%; t_p1 = 4,7; t_п = 8,4,

где  – максимальное перерегулирование; t_p1 – время первого достижения функцией нового заданного значения; t_п – полное время регулирования, т. е. время вхождения регулируемой величины в область значений, отличающихся не более чем на ±2% от величины скачка задающего возмущения. Так как при этом переходный процесс в системе регулирования представляет собой колебательное звено, то оптимальному отклику системы при y_3(t) = 1(t) соответствует коэффициент затухания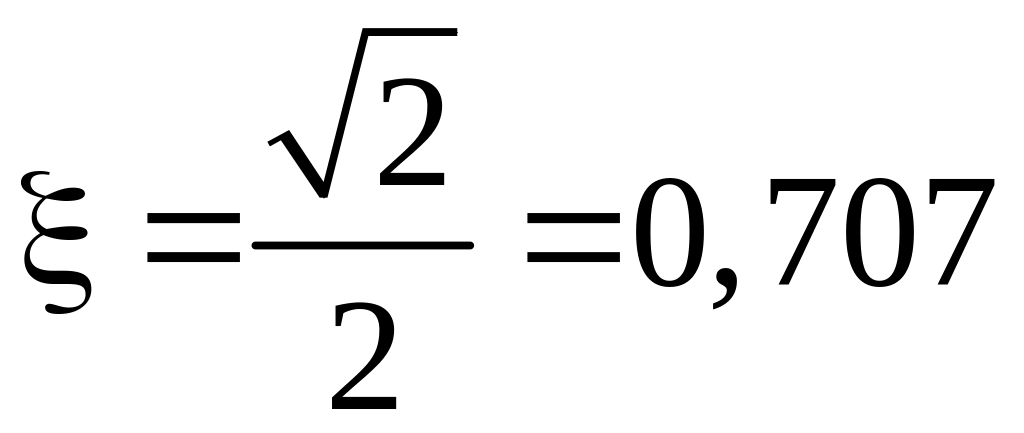 обеспечивающий в соответствии с графиком, приведенным на рис. 2.3, минимальное время регулирования. Причем при других значениях коэффициента демпфирования  основные показатели качества переходной характеристики у₁(t) однозначно определяются по графикам, приведенным на рис. 2.3 (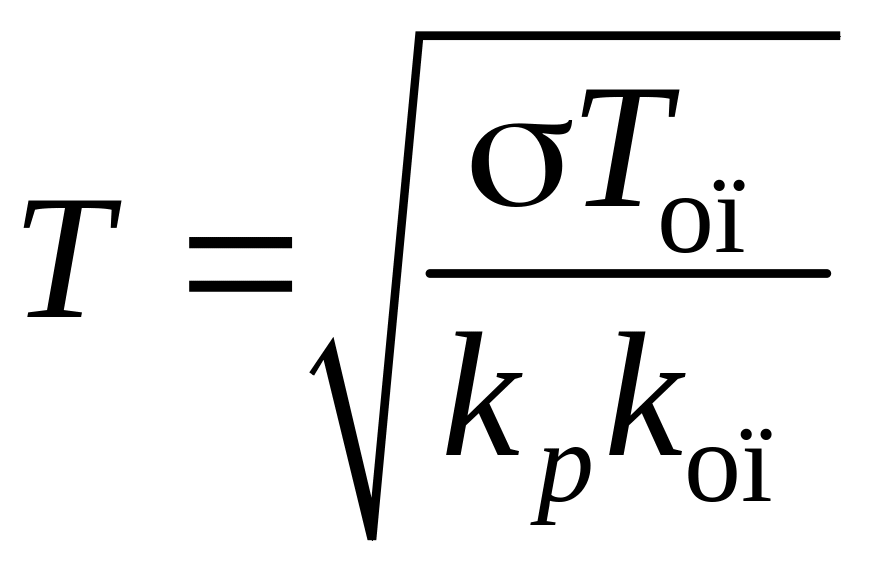 – эквивалентная постоянная времени колебательного звена; М – показатель колебательности; – относительное время полного регулирования).

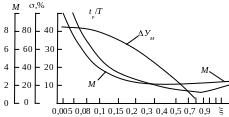
Рис. 2.3. Зависимость максимального перерегулирования , относительного времени регулирования t_p /T и показателя колебательности системы М

от коэффициента демпфирования

Если при этом через М_у1 обозначить заданное значение показателя колебательности промежуточной регулируемой величины y₁, то относительный коэффициент усиления ПИ-регулятора можно определить:

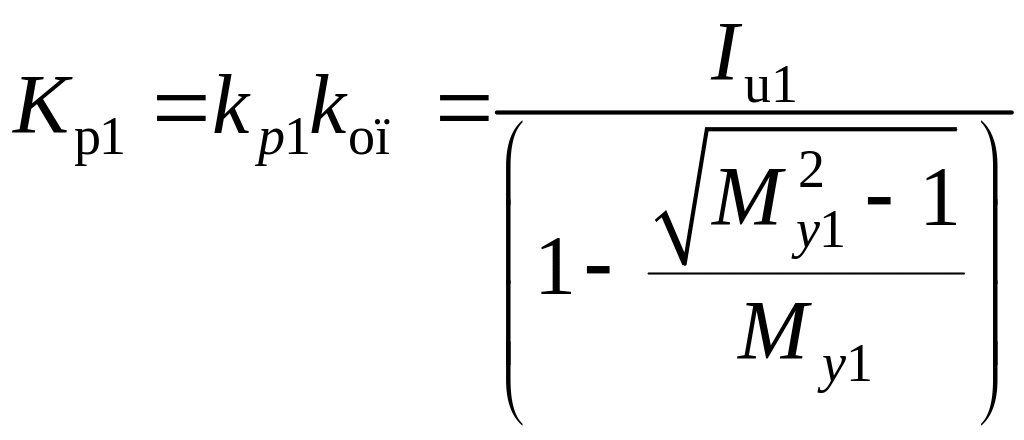; (2.44)

где .

Таблица 2.3

Оптимальные значения параметров динамической настройки КСАР при замене внутреннего контура эквивалентной передаточной функцией

Структура регуляторов	Передаточные функции:		Соотношения между параметрами регулятора и объекта	Условные обозначения
	регулятора	модели участка объекта
1	2	3	4	5
1. СР: 1.1. ПИД1			; ;	; ;
1.2. ПИ1			;
1.3. ПИ1

Продолжение табл. 2.3

1	2	3	4	5
1.4. ПИ1
2. КР: 2.1. ПИДД2		; ;	; ;

Окончание табл. 2.3

1	2	3	4	5
2.2. ПИД2			;	; ; ;
2.3. ПИ2			;

Формулы (2.20) и (2.18) оптимальной динамической настройки ПИ- и ПИД-регуляторов и объекта с передаточной функцией (2.42) путем замены p на r применимы для опережающих участков объектов с запаздыванием:

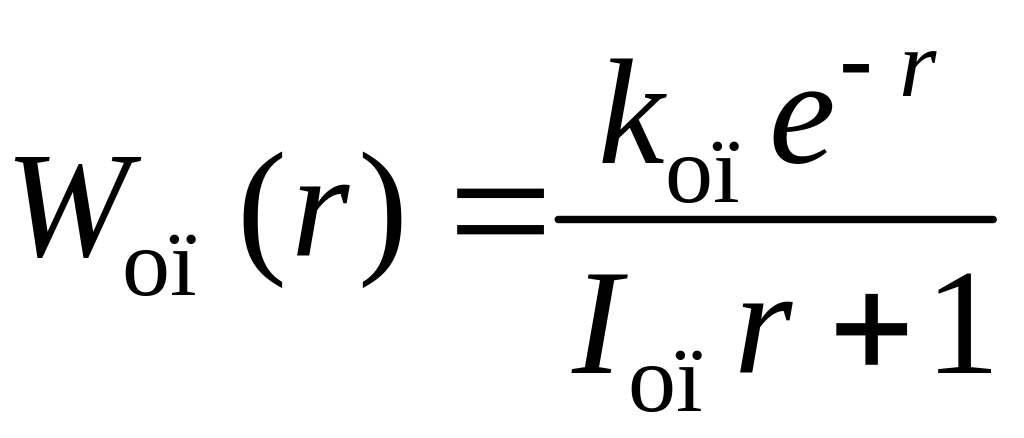(2.45)

где 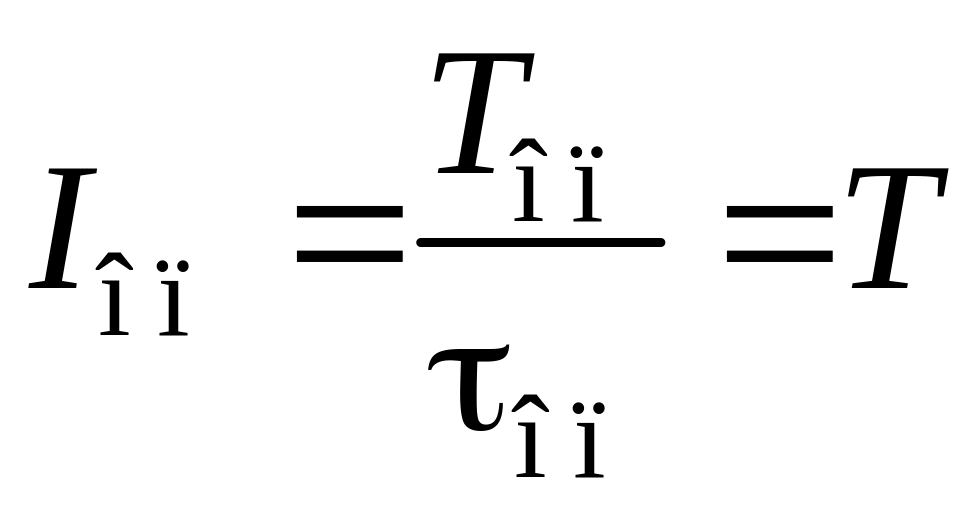– относительная постоянная времени опережающего участка; r = _опp – новый оператор Лапласа.

Для объекта с передаточной функцией (2.45) параметры оптимальной динамической настройки ПИ-регулятора можно рассчитать также по формулам Гурецкого:

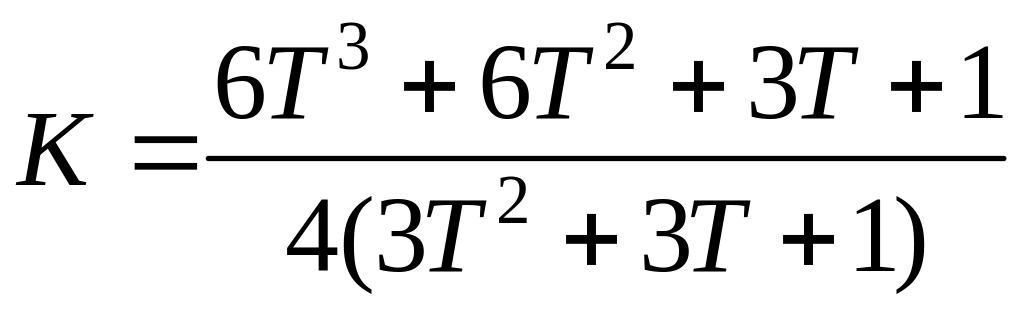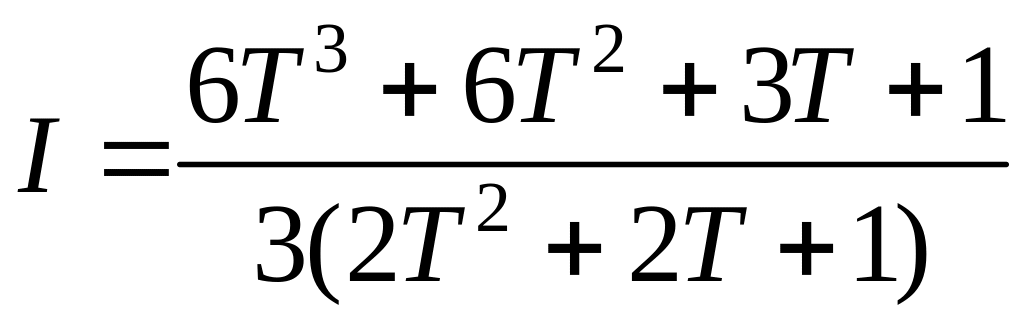; . (2.46)

Проведенные численные расчеты по формулам (2.46) и (2.44) параметров динамической настройки ПИ-регуляторов для объектов с относительной постоянной времени Т = 120 при М_у1 = 1 показали хорошую сходимость результатов. Так, например, если для объектов с относительной постоянной времени Т = 2 относительная разница в определении относительного значения коэффициента усиления регулятора k не превышает 3,9%, времени интегрирования  1,28%, то при Т = 10 эта разница уменьшается до 0,16% для k и 0,02% для Т = 1. Формулы (2.44) в относительных величинах при М_у1 = I имеют вид:

. (2.47)

При этих настройках ПИ-регулятора оптимальный переходный процесс в системе с запаздыванием при отработке скачка задания имеет величину перерегулирования, равную y_м = 4,3%, однако несколько уменьшается значение времени регулирования:

t_p1 = 3,7_оп; t_п = 6,1_оп.

Предложенный метод определения оптимальных значений параметров настройки ПИ- и ПИД-регуляторов, исходя из минимизации интеграла от суммы квадрата ошибки регулятора и квадрата производной ошибки c соответствующим весом, позволяет с минимальными затратами определить прямые оценки качества процесса регулирования.

Результаты расчета параметров оптимальной динамической настройки ПИ- и ПИД-регуляторов стабилизирующего контура для опережающего участка с передаточными функциями (2.42) и (2.46) сведены в табл. 2.3.

Так как для внешнего контура регулирования подчиненный ему внутренний контур в целом следует считать объектом регулирования, передаточная функция которого может быть представлена в виде

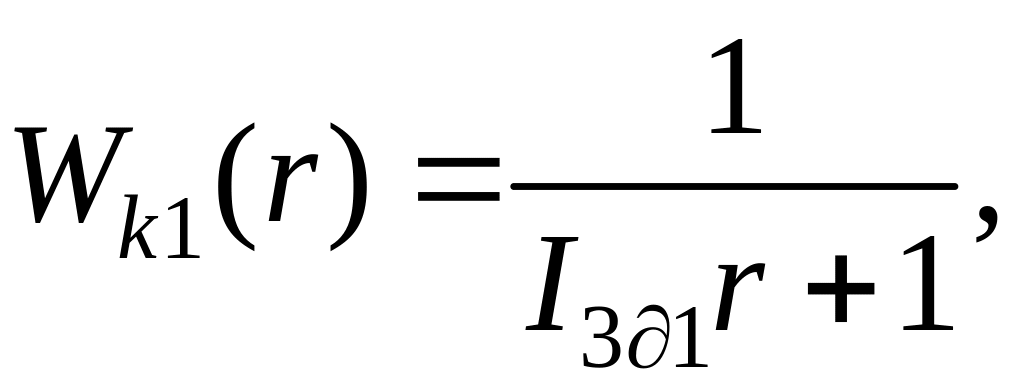(2.48)

то структурную схему, изображенную на рис. 2.2, приведем к виду, представленному на рис. 2.4.

Тогда для корректирующего регулятора передаточную функцию эквивалентного объекта можно представить в виде

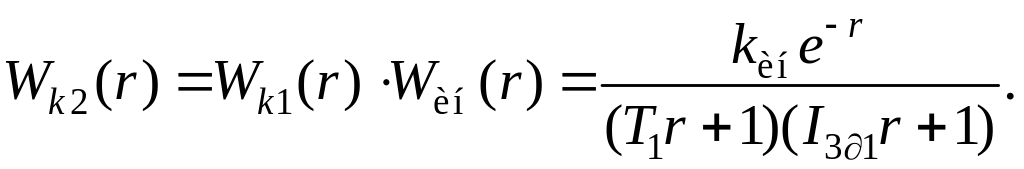(2.49)

В результате получим следующие соотношения для расчета относительных параметров динамической настройки ПИД-регулятора, оптимальных относительно эквивалентного внешнего возмущения:

_;

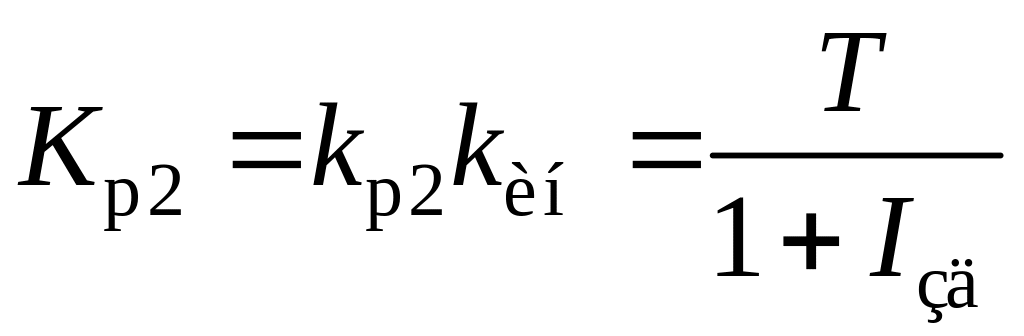_; (2.50)

где  относительное время разгона инерционного участка объекта; K_p2 – относительный коэффициент усиления корректирующего регулятора; k_p2 – абсолютное значение коэффициента усиления регулятора; I_и2 – относительная постоянная времени интегрирования Т_и2;

I_1, I_2 – соответственно относительные постоянные времени первого и второго дифференцирования.

Полученные результаты по расчету параметров динамической настройки корректирующих регуляторов также сведены в табл. 2.3.

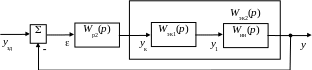
Рис. 2.4. Структурная схема САР, приведенная к одноконтурной путём

внутреннего контура (рис. 2.2) эквивалентным звеном

Рис. 2.5. Структурная схема каскадной САР как эквивалента системы регулирования

с дифференцированием промежуточного сигнала

Другой порядок расчета параметров оптимальной динамической настройки каскадной САР основан на том, что ее структурная схема (рис. 2.2) формально может быть заменена структурной схемой (рис. 2.5), эквивалентной приведенной на рис. 2.1, а схеме для САР с дифференцированием промежуточного сигнала, если обозначить:

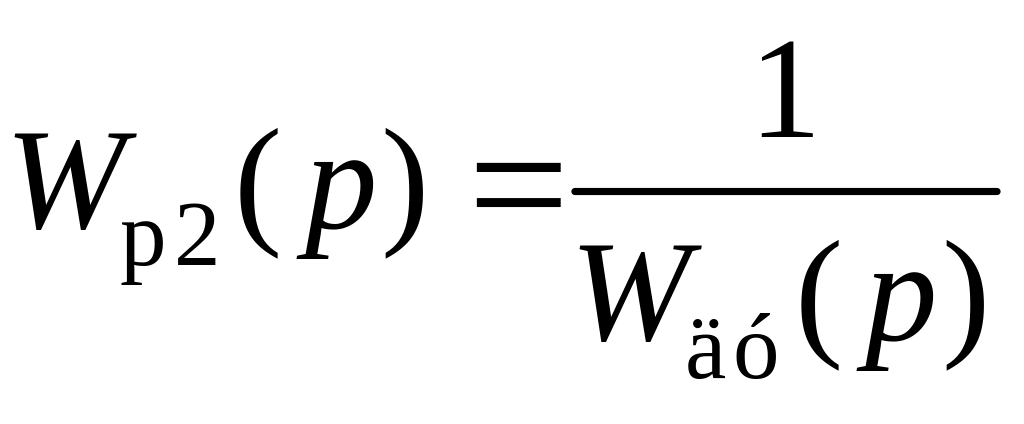; , (2.51)

где W_p1(p), W_p2(p) = W_(p)W_F(s)  передаточные функции стабилизирующего и корректирующего регуляторов (рис. 2.2);

W_p, W_ду – передаточные функции регулятора и дифференцирующего устройства (рис. 2.1, а).

Рассмотрим, при какой структуре и параметрах динамической настройки стабилизирующего и корректирующего регулятора справедливы соотношения (2.51).

Пусть передаточная функция имеет вид реального дифференциатора. Тогда передаточную функцию внутреннего контура каскадной САР представим в виде:

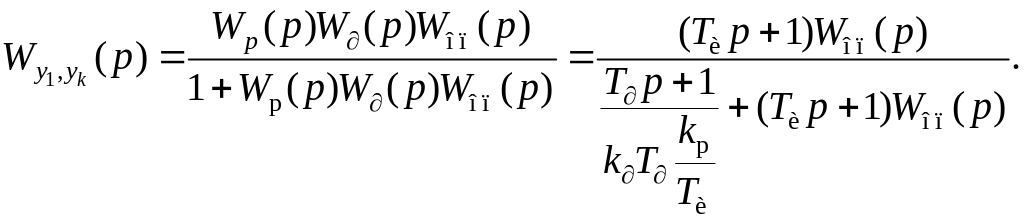(2.52)

С другой стороны, ее можно выразить через передаточную функцию стабилизирующего ПИ₁-регулятора (СР):

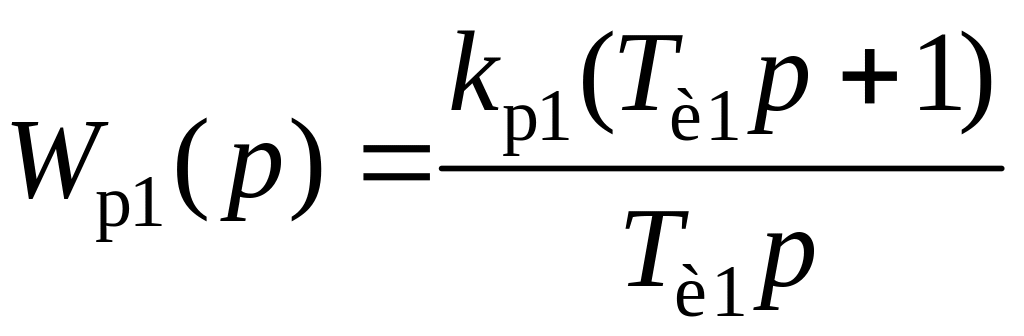(2.53)

где k_p1 – коэффициент усиления; Т_и1  постоянная времени интегрирования СР:

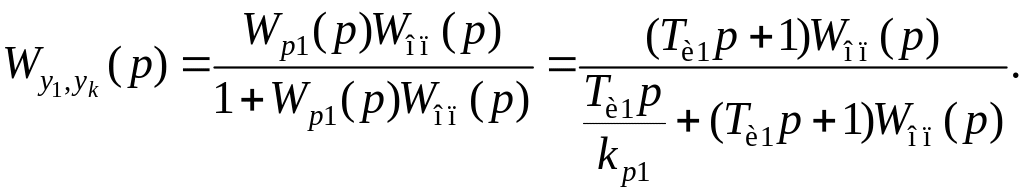(2.54)

Приравняв передаточные функции (2.52) и (2.54), находим условия приближенного выполнения (2.53) для стабилизирующего регулятора:

; (2.55)

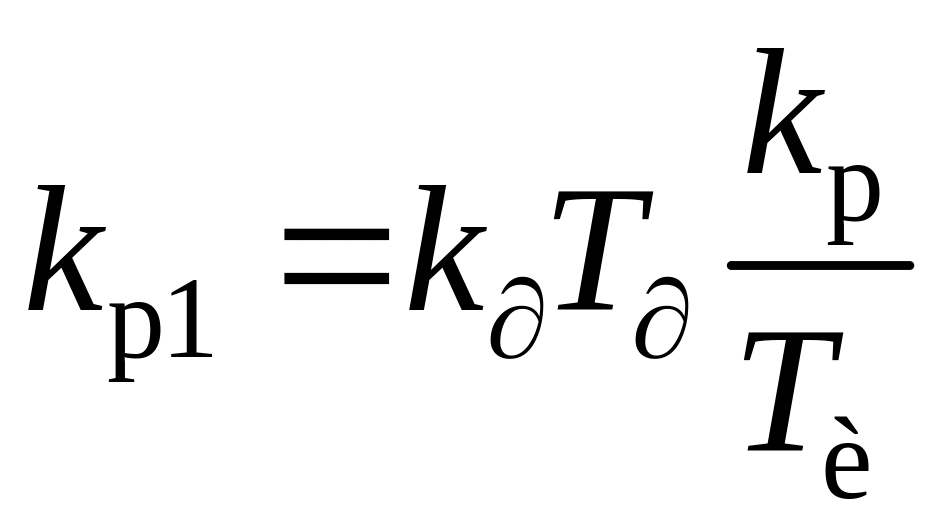, (2.56)

для корректирующего регулятора:

; (2.57)

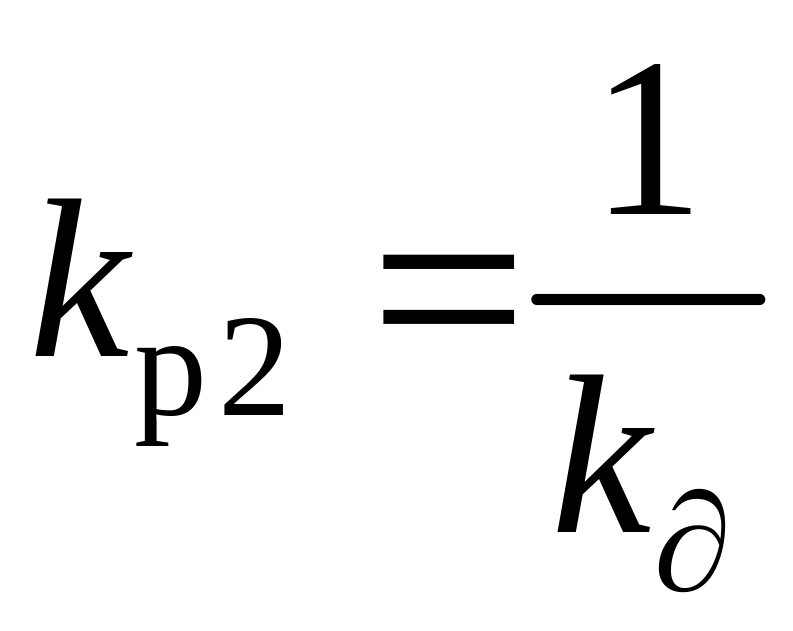. (2.58)

Вместе с тем видно, что типовая схема КСАР со стабилизирующим ПИ₁-регулятором будет эквивалентна схеме САР с дифференцированием промежуточного сигнала только при достаточно большой величине 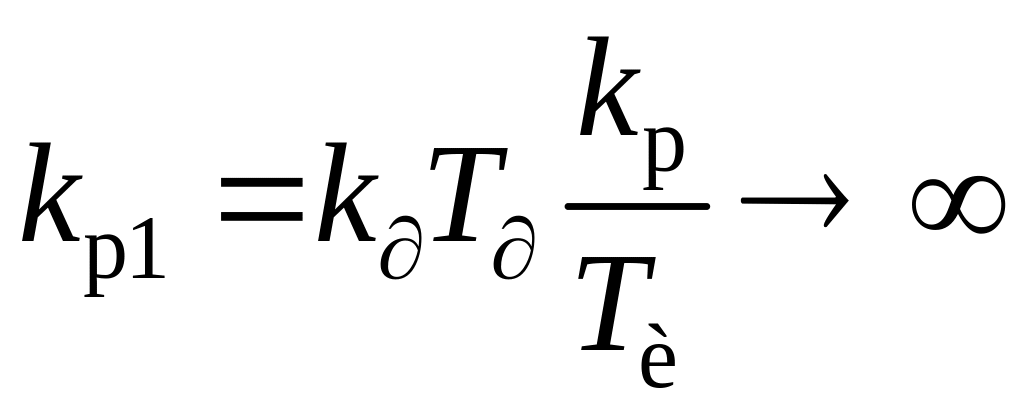. Кроме того, из соотношения (2.56) следует, что только в частном случае при условии, что Т_д = Т_и коэффициент усиления СР может быть определен по формуле

. (2.59)

В связи с этим для объектов, допускающих статическую ошибку регулирования промежуточной величины y₁(t), в качестве стабилизирующего регулятора используют П- или ПИД-регулятор, настраивая его на апериодический переходный процесс с наименьшей длительностью.

Если в КСАР имеются оба регулятора с интегральной составляющей в законе регулирования, то для того чтобы сделать стабилизирующий регулятор статическим, введем жесткую обратную связь (ЖОС) по положению регулирующего органа с передаточной функцией k_ос (рис. 2.6).

Из анализа рис. 2.6 и 2.7 следует очевидное соотношение для САР:

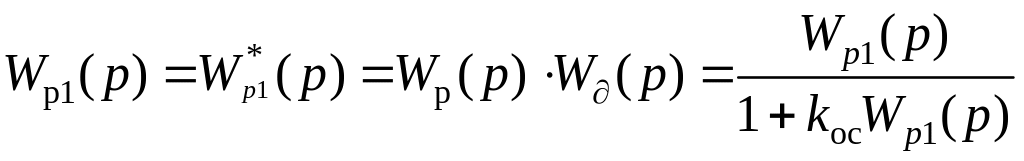
или

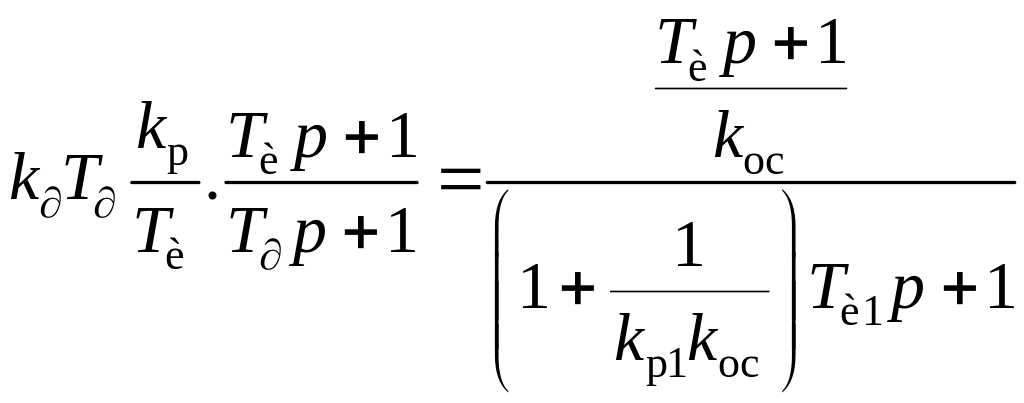_. (2.60)

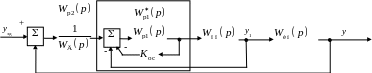
Рис. 2.6. Структурная схема каскадной САР с двумя ПИ-регуляторами

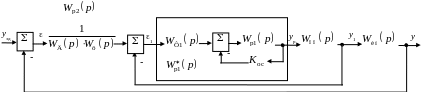
Рис. 2.7. Структурная схема каскадной САР с корректирующим ПИД-регулятором

Таблица 2.4

Оптимальные значения параметров динамической настройки КСАР как аналога САР с дифференцированием промежуточного сигнала

Структура регуляторов	Передаточные функции		Соотношения между параметрами и	Условные обозначения
		модели участков объекта
1	2	3	4	5
1.1. КР: ПИД2			; ;	; ; ; ;

Продолжение табл. 2.4

1	2	3	4	5
1.2. СР: Ф1ПИ1ЖОС			; ;	; ; ;
2.1. КР: ПИ2

Окончание табл. 2.4

1	2	3	4	5
2.2. СР: ПИ1
3.1 КР: ПИ2	;		;
3.2. СР: ПИ1 с ЖОС			; ;	;

Из уравнения (2.56) находим параметры динамической настройки внутреннего контура:

; (2.61)

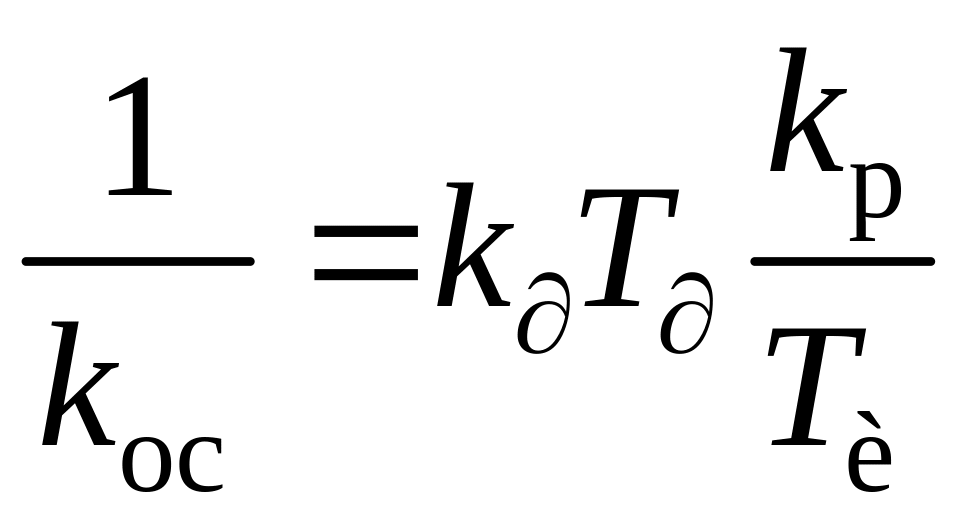; (2.62)

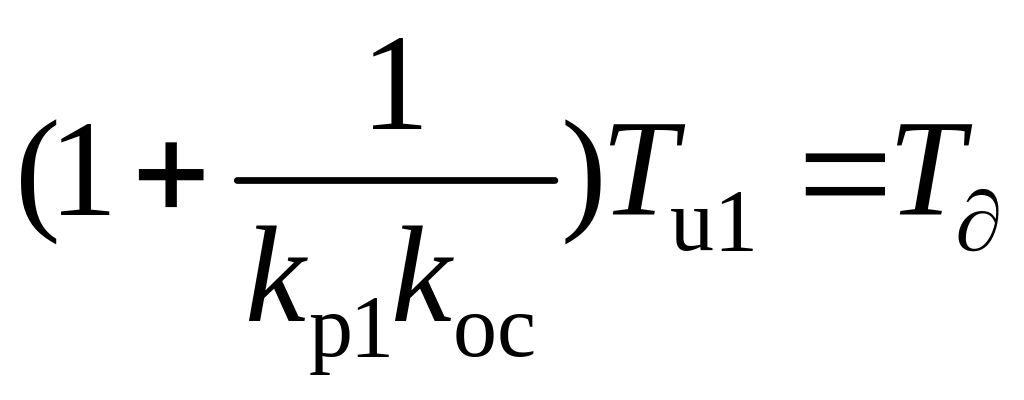. (2.63)

Если дифференцирующее устройство представлено последовательным соединением реального дифференциатора с фильтром, то условия (2.51) требуют выполнения структурной схемы КСАР в виде схемы, изображенной на рис. 2.7. В этом случае корректирующий регулятор (КР) осуществляет ПИД-алгоритм регулирования:

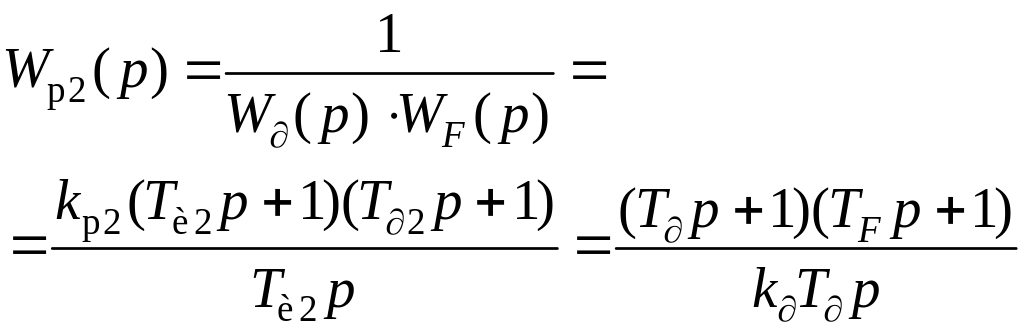(2.64)

Из уравнения (2.64) видно, что параметры настройки ПИД-регулятора КСАР определяют через параметры САР с дифференцированием промежуточного сигнала следующими соотношениями:

; Т_и2 = Т_д; Т_д2 = Т_ф, (2.65)

где k_р2 – коэффициент усиления; Т_ф – постоянная времени фильтра;

Т_и2, Т_д2 – постоянные времени интегрирования и дифференцирования.

При этом передаточная функция стабилизирующего регулятора равна:

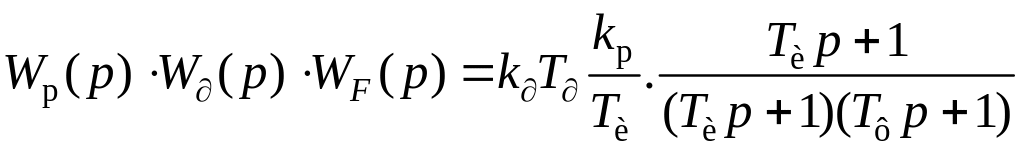. (2.66)

С другой стороны, передаточную функцию СР (2.56) можно реализовывать передаточной функцией вида

, (2.67)

где Y_p(p), E₁p – соответственно изображения у_р(t) регулирующего воздействия СР и ошибки регулирования e₁(t) стабилизирующего контура.
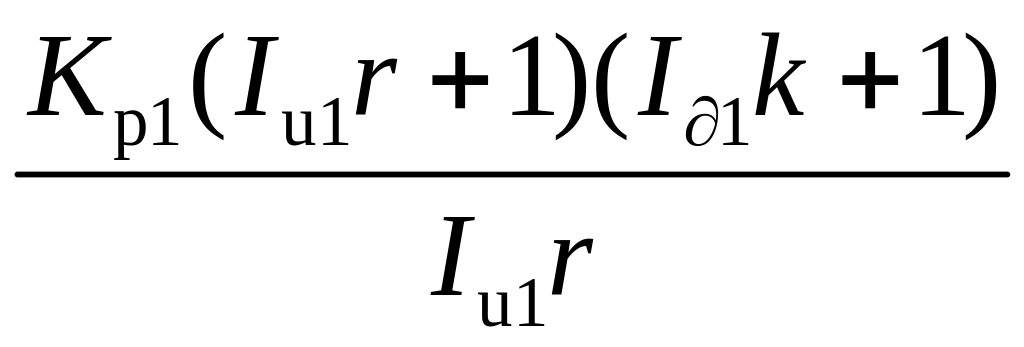
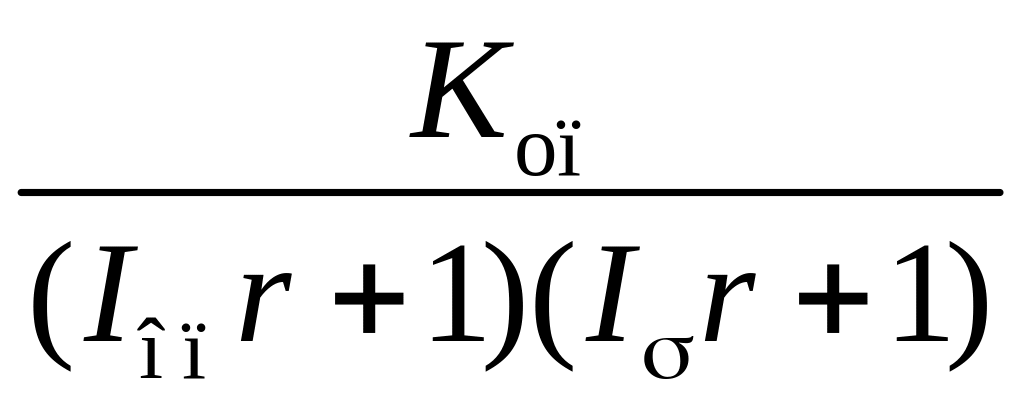
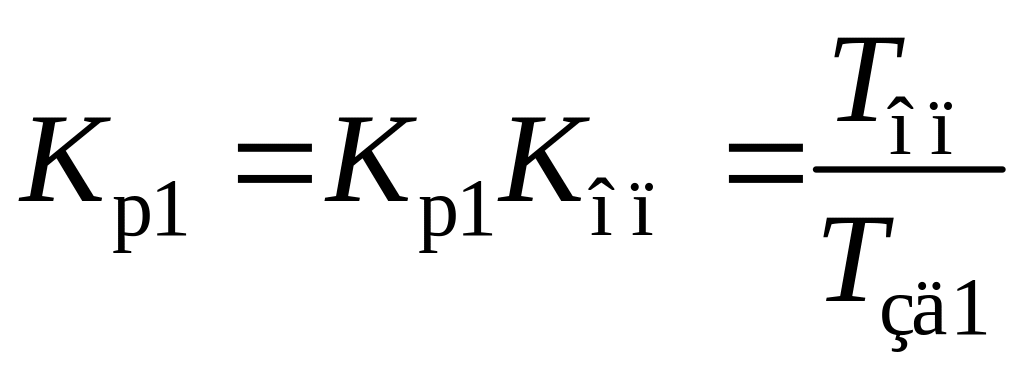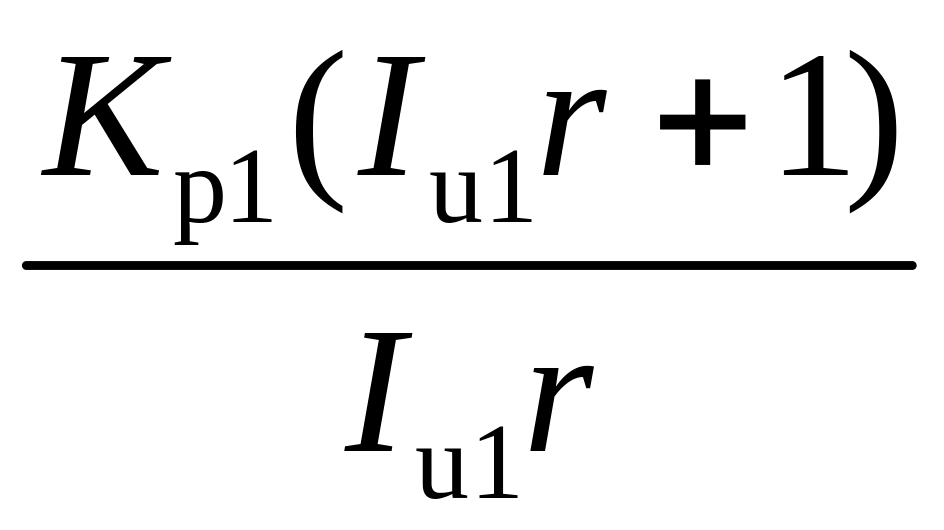
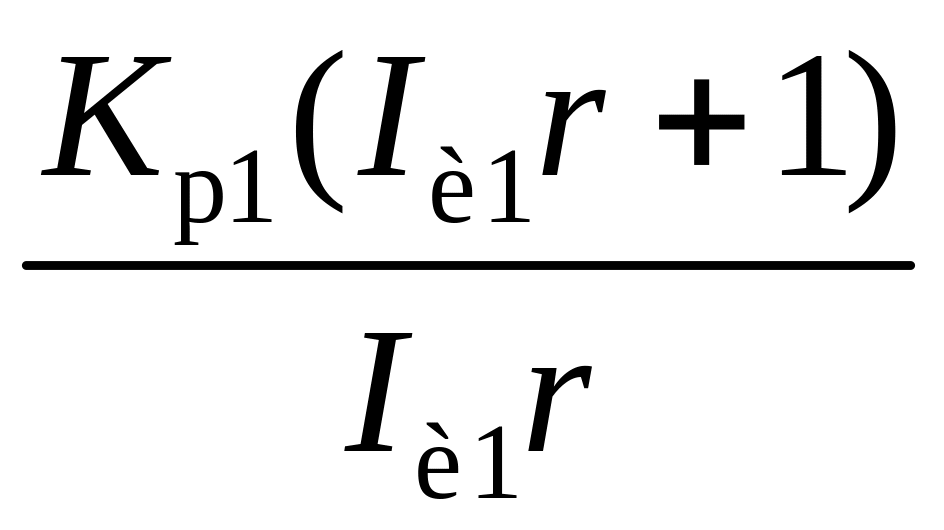
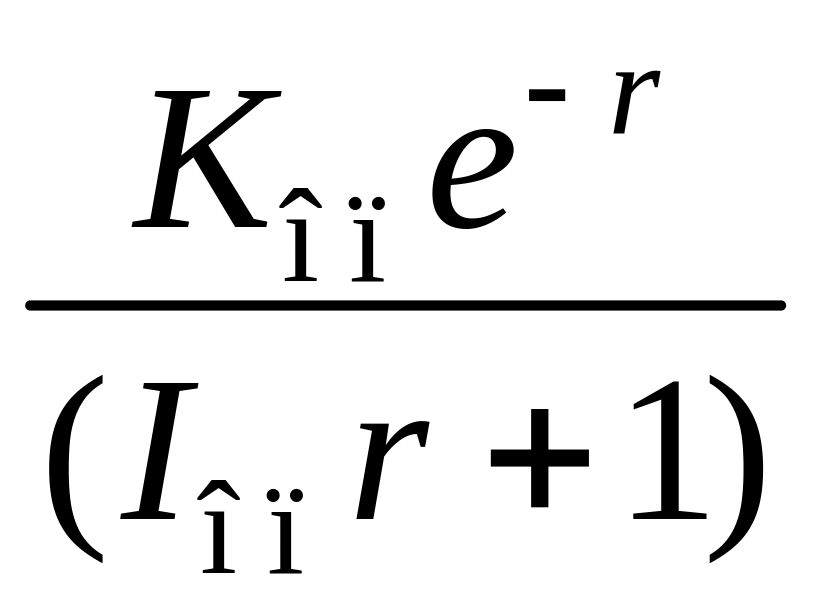
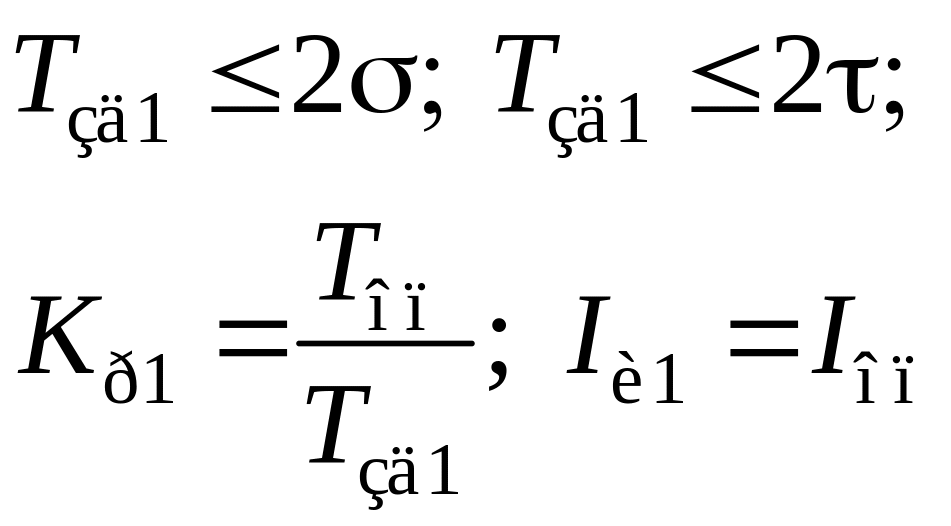
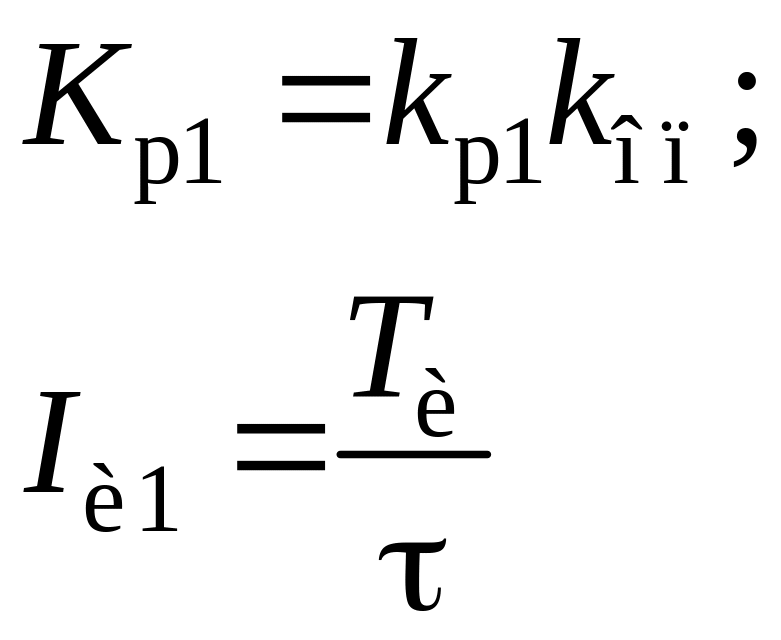
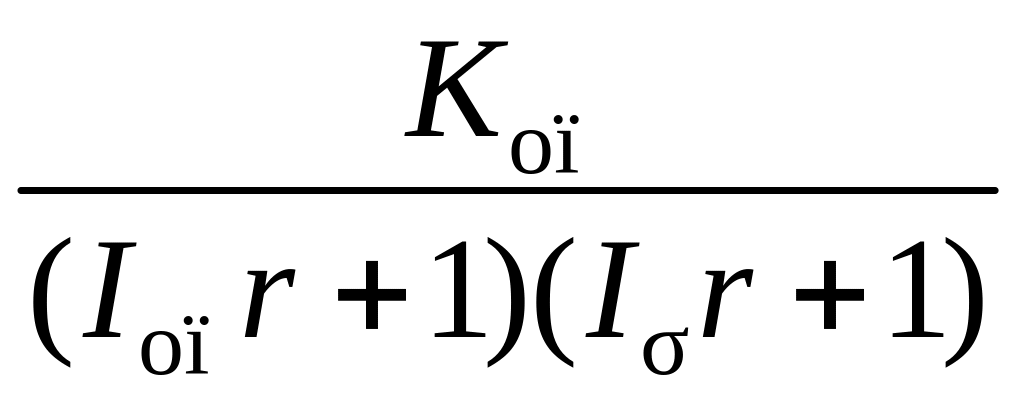
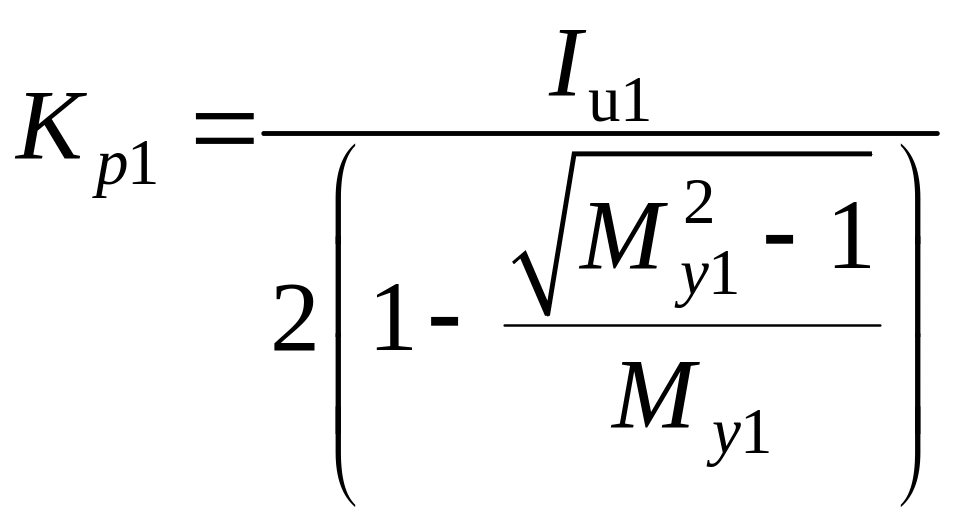
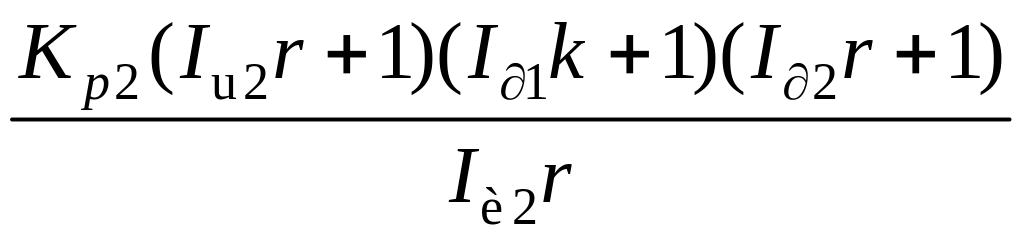
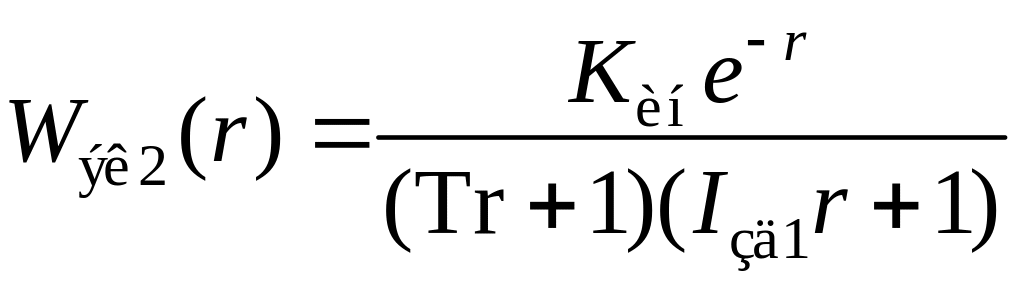
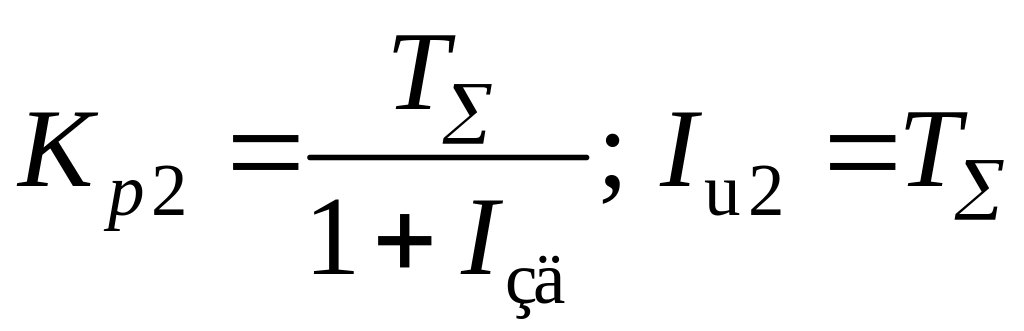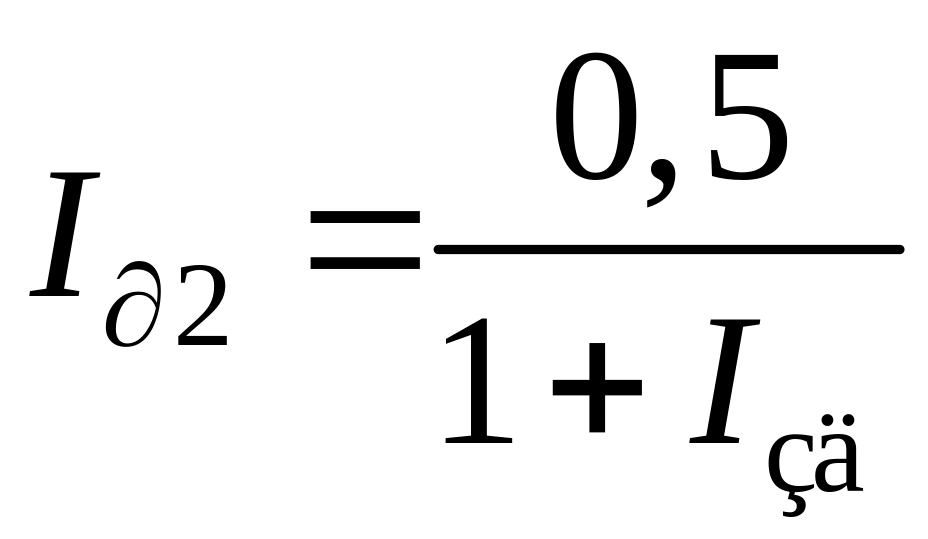
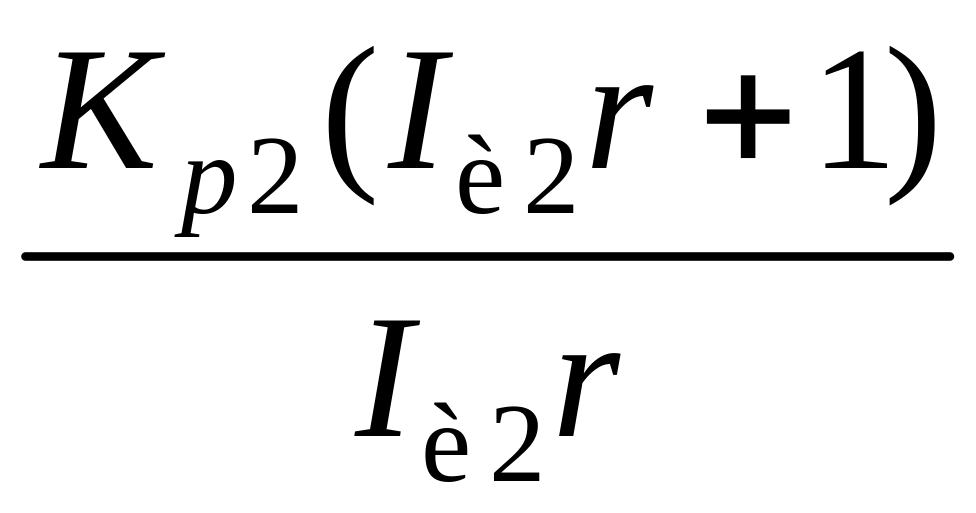
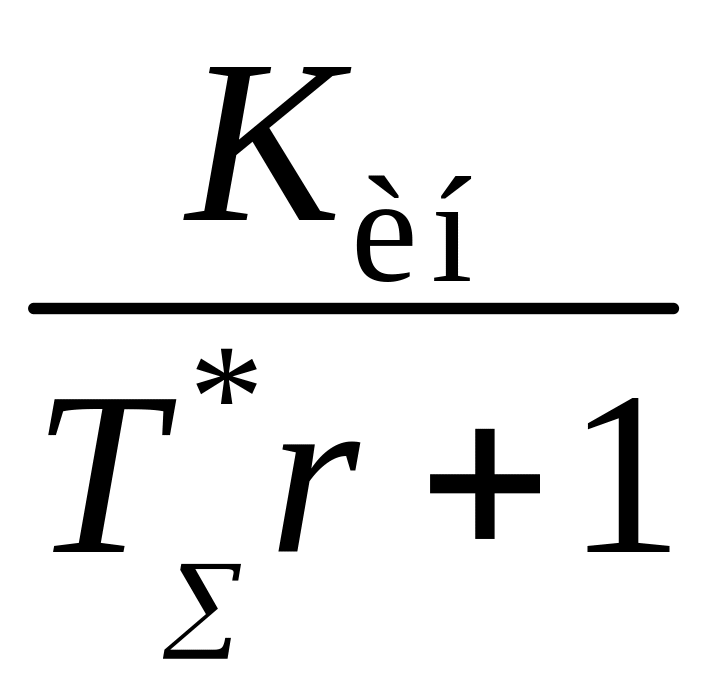
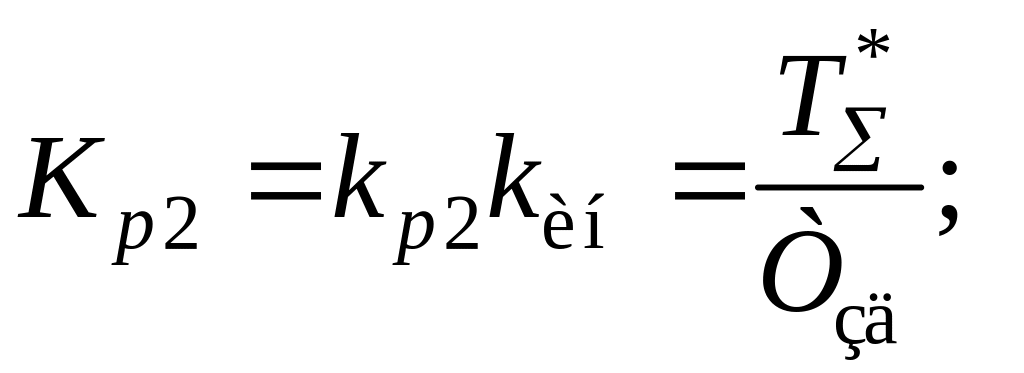
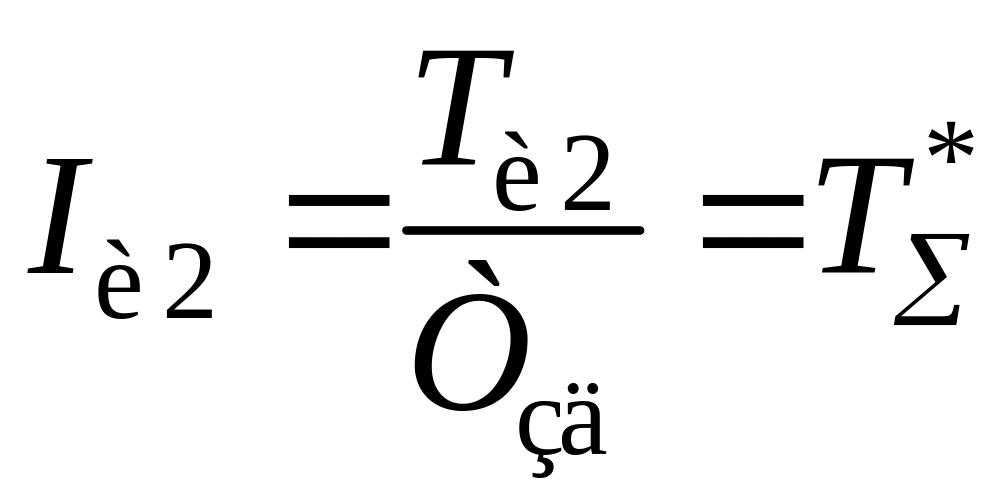
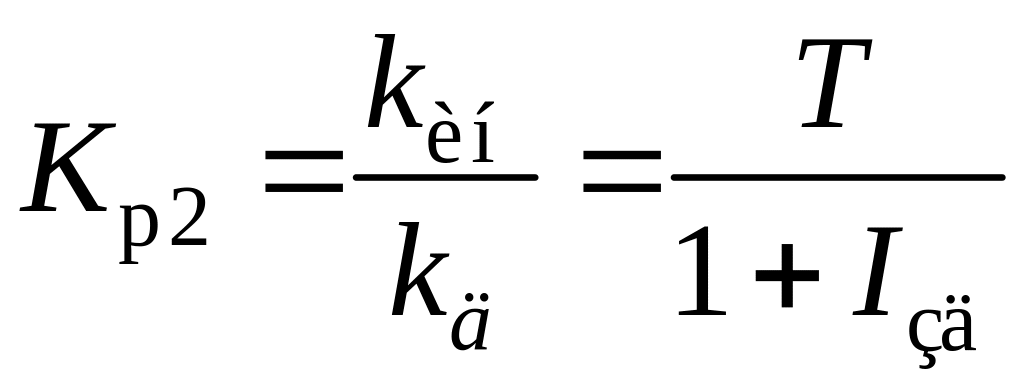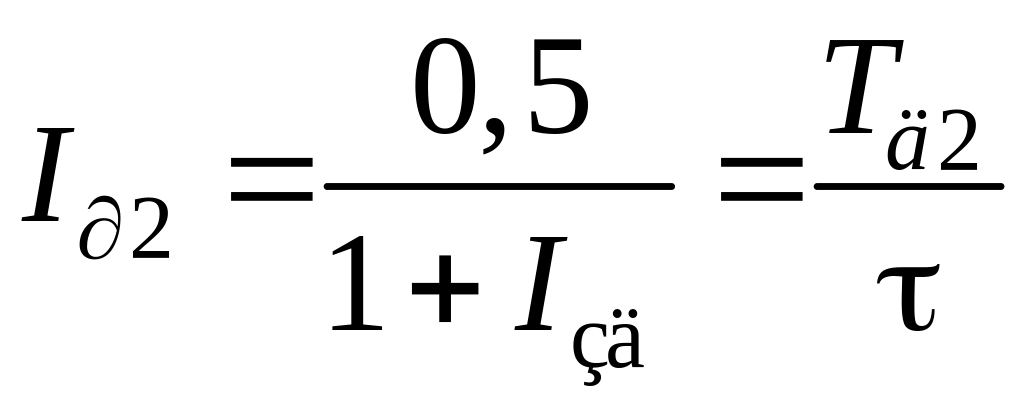
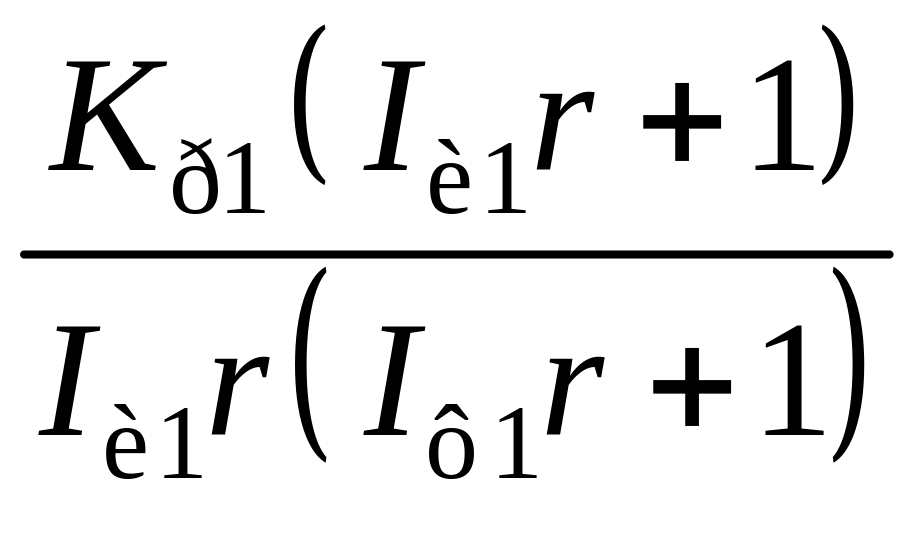
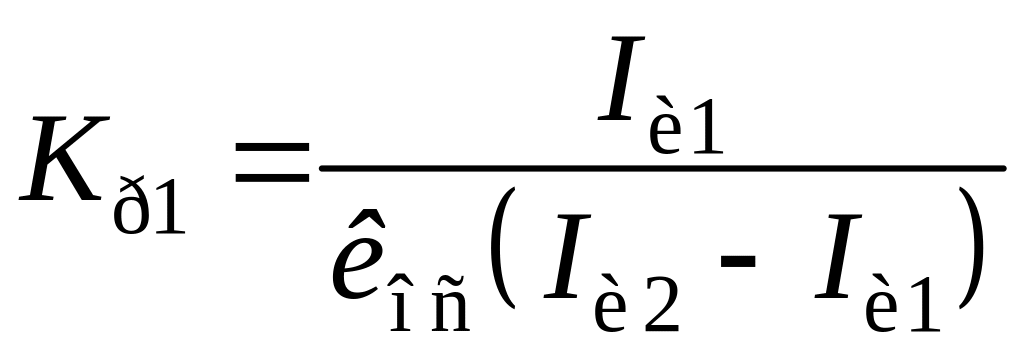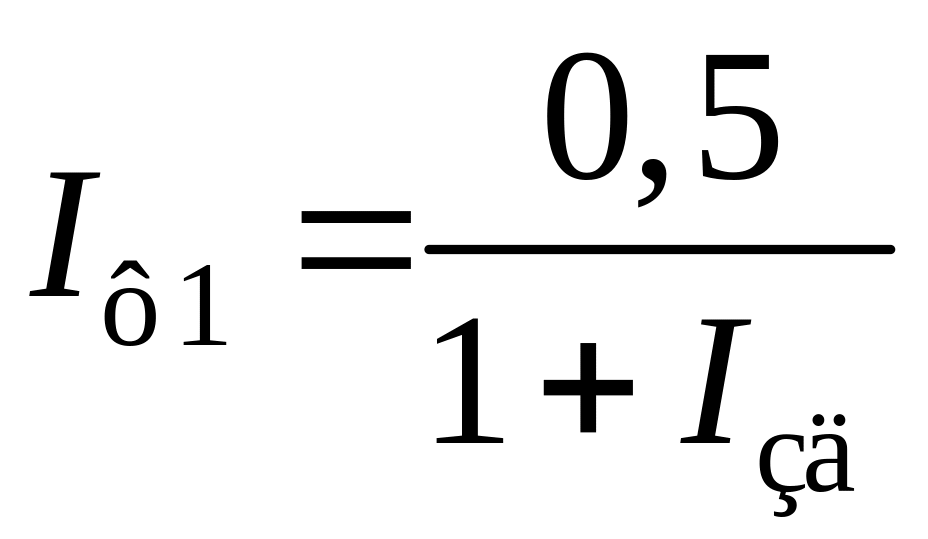
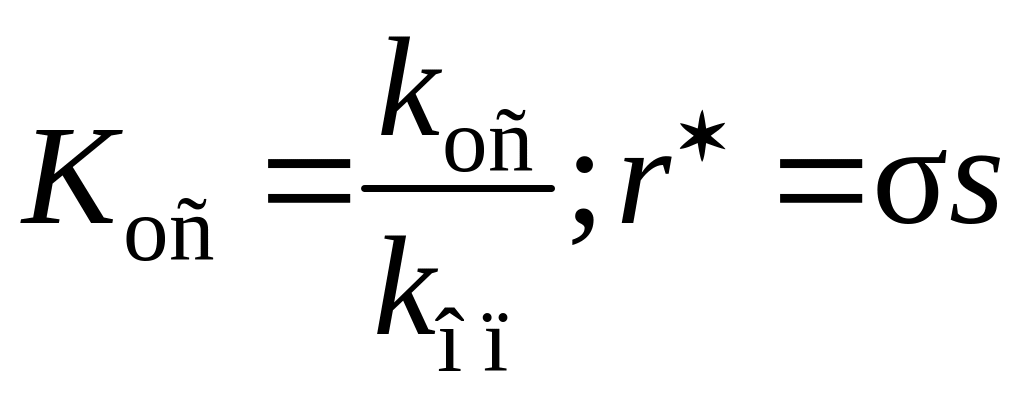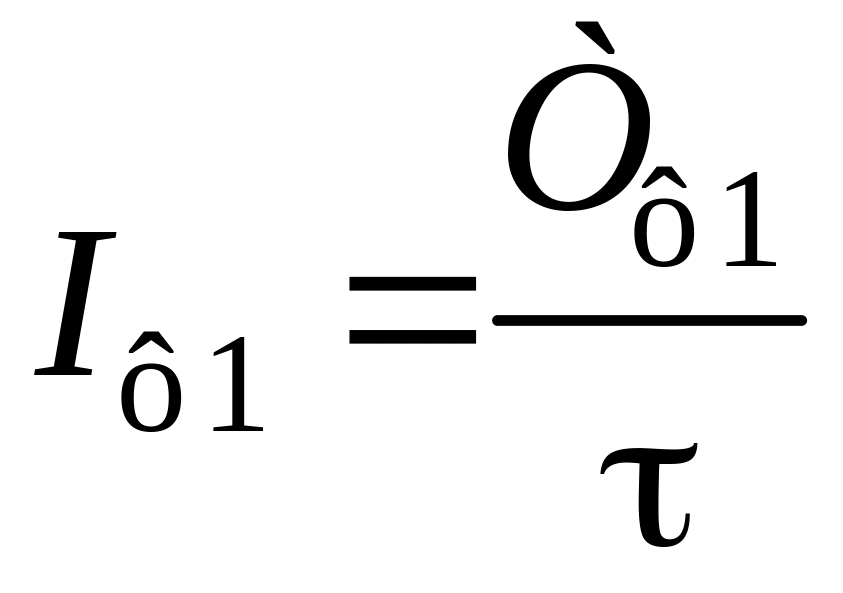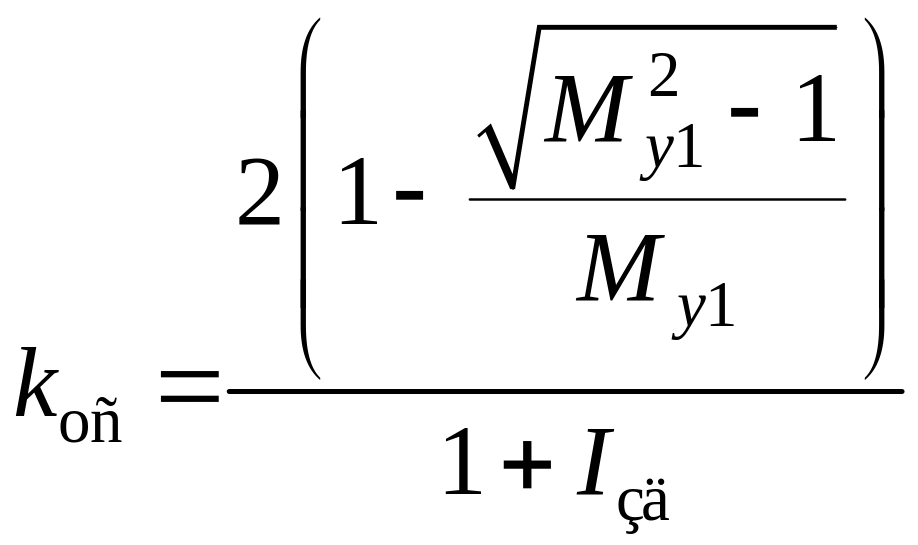
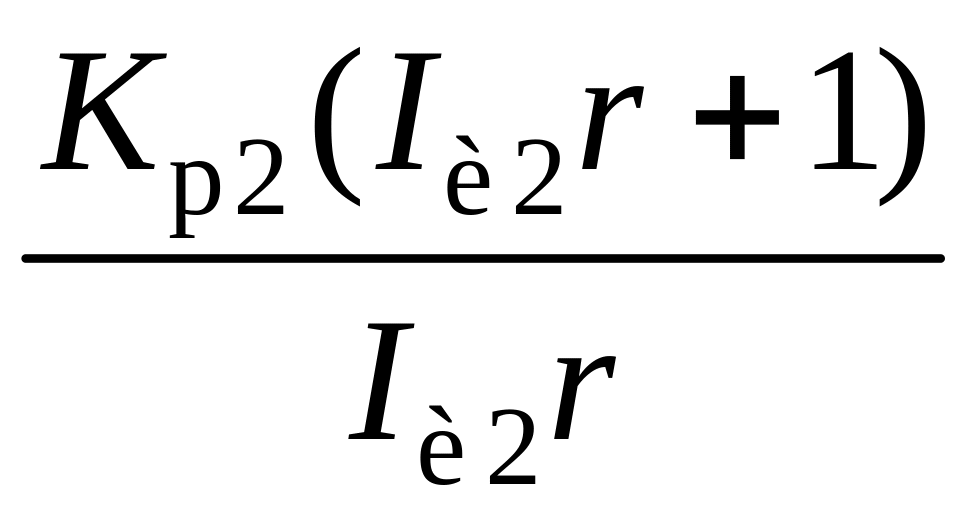
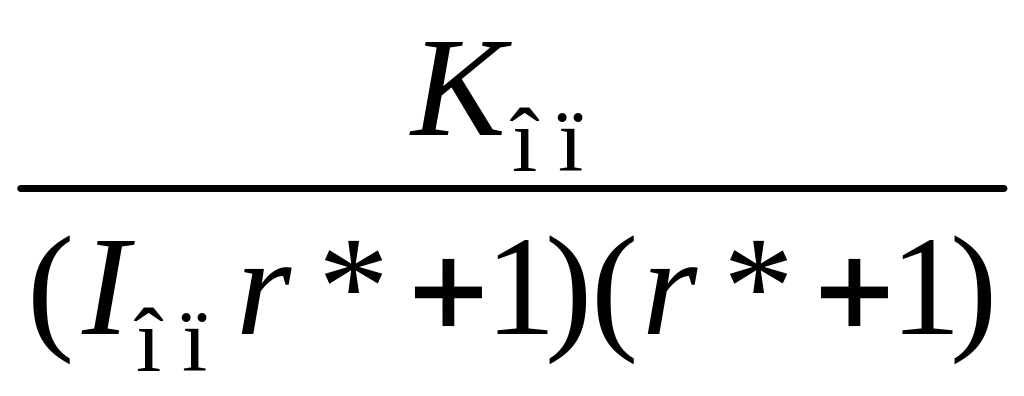
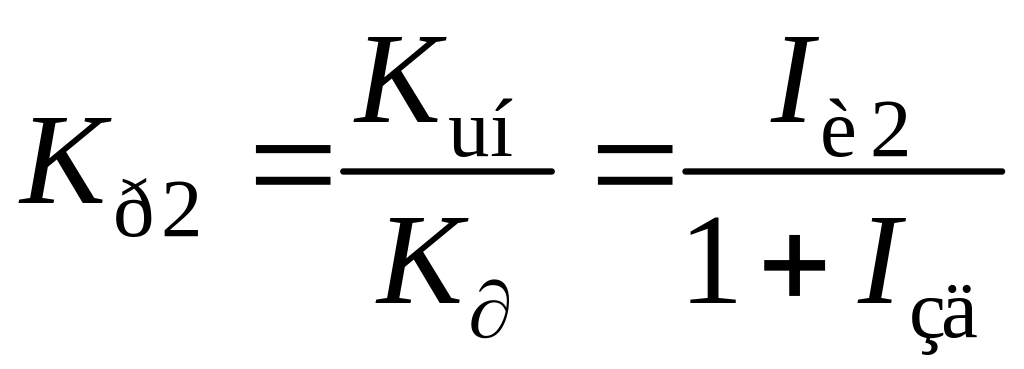
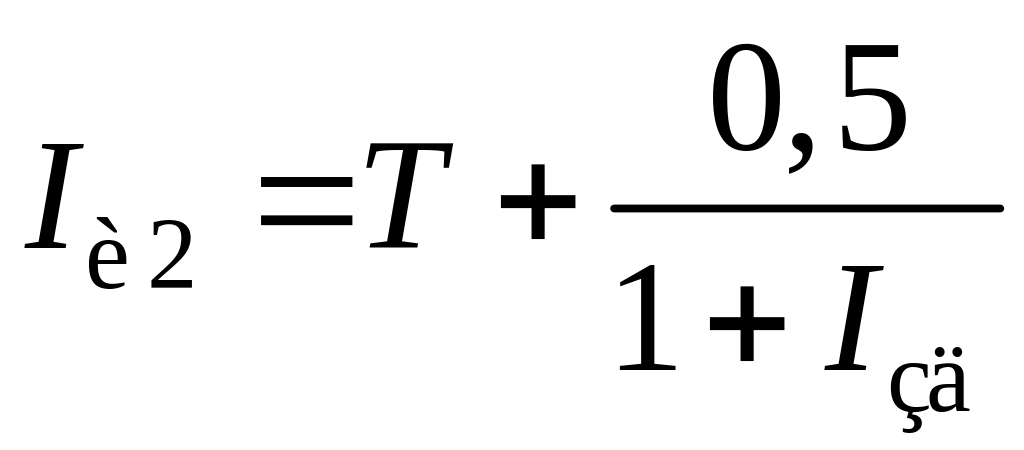
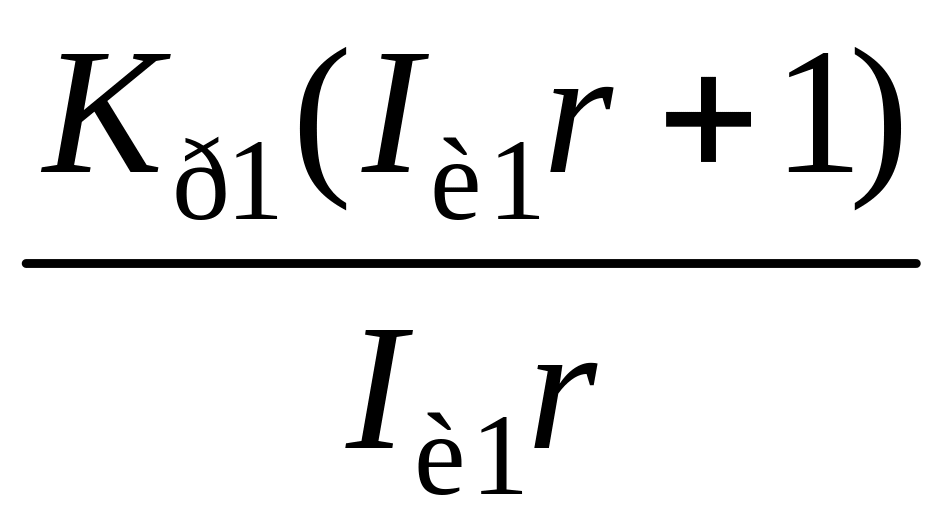
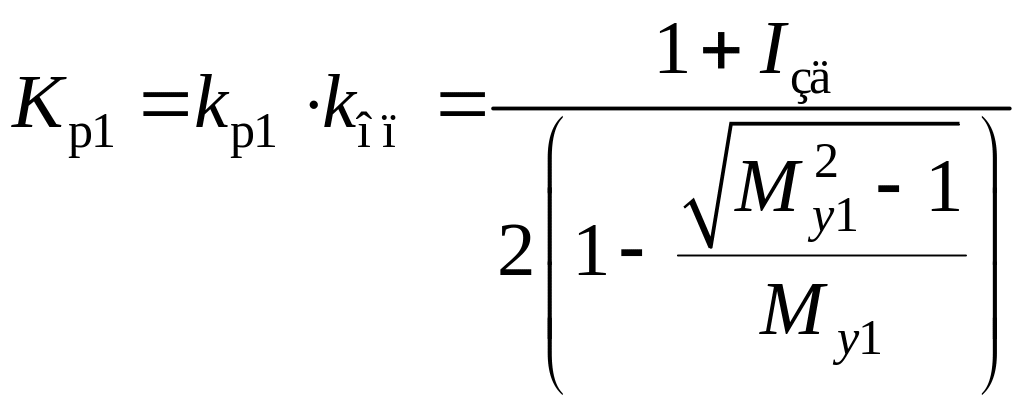
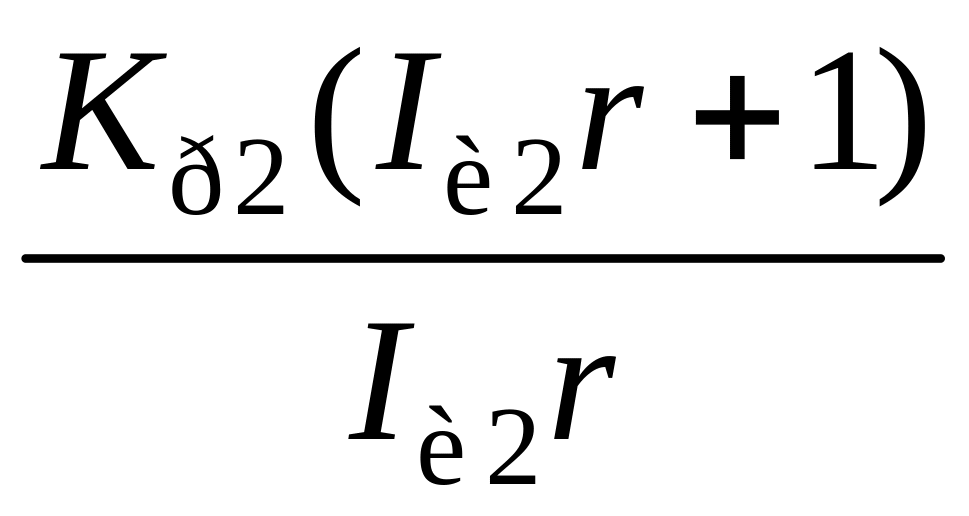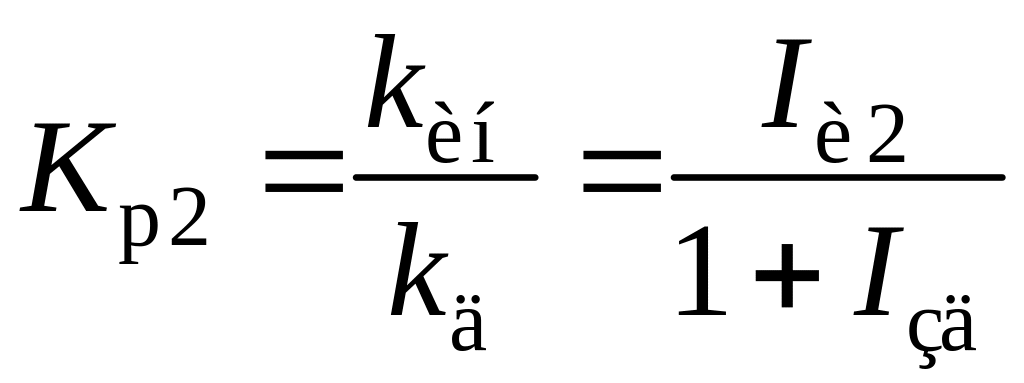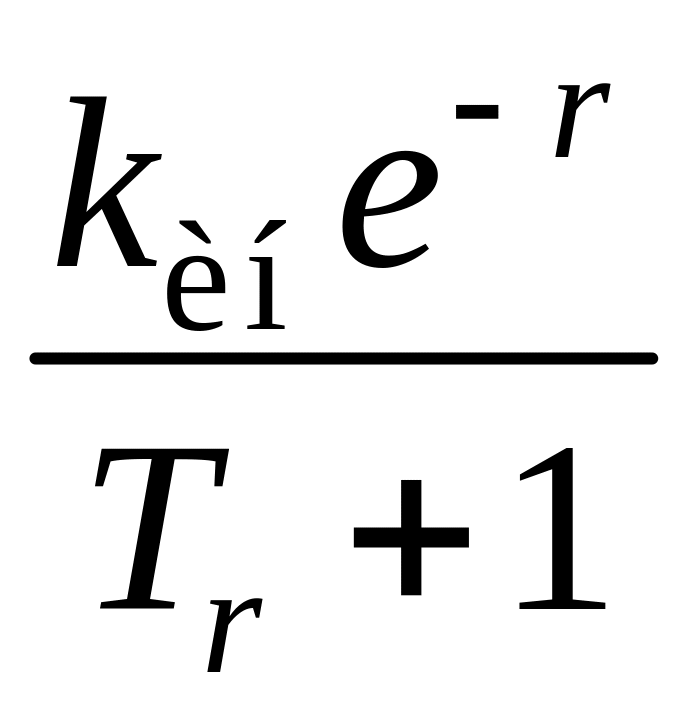
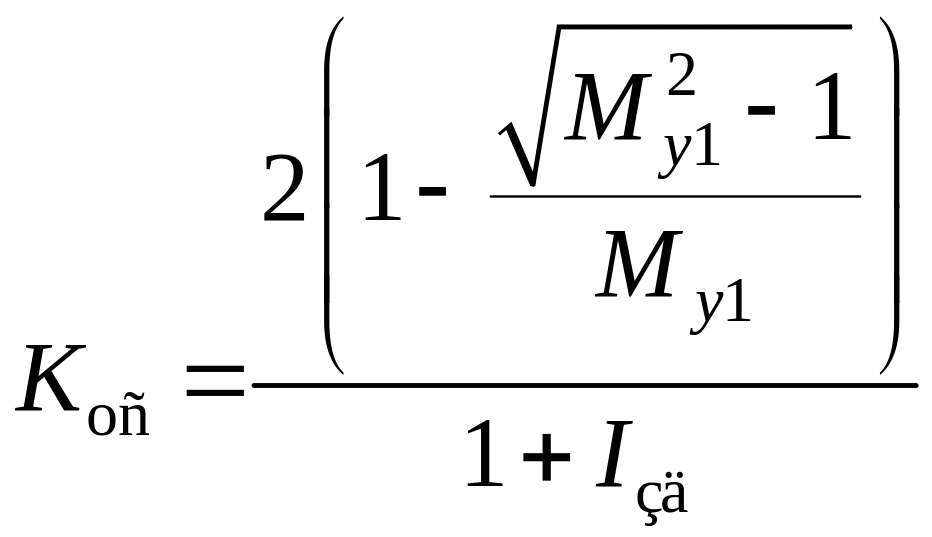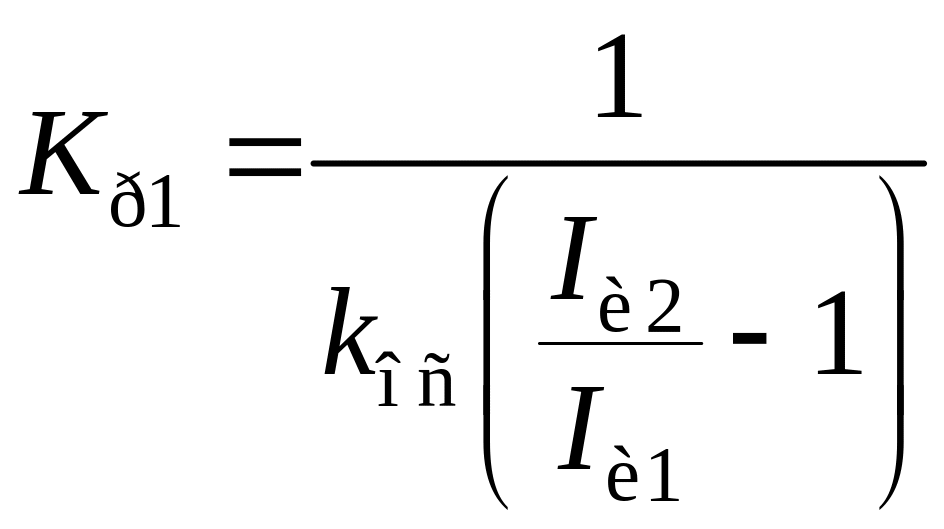
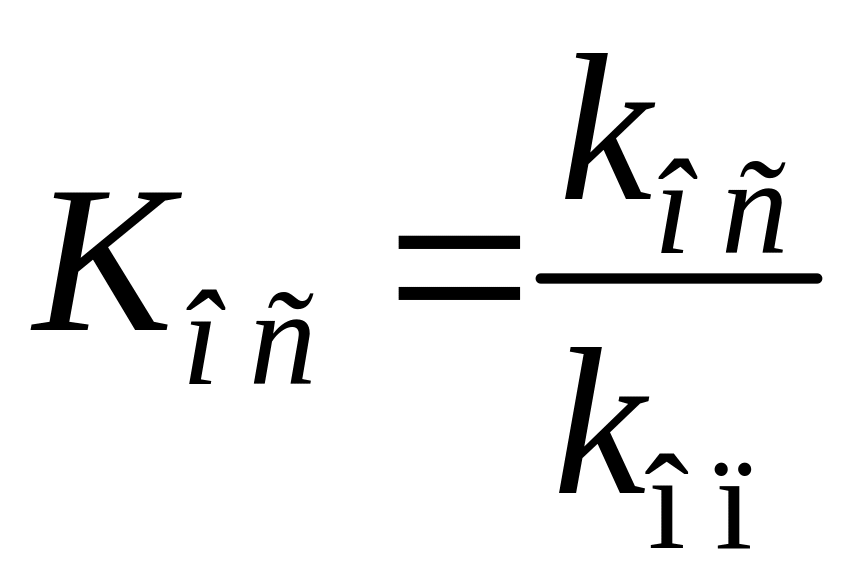