2.4. Расчет параметров регулятора на основе критерия оптимального модуля

Этот критерии предполагает, что амплитудная характеристика не имеет резонансного пика, а полоса пропускания для полезного сигнала должна быть как можно более широкой. Пусть выбранный типовой регулятор имеет один настраиваемый параметр. Установлено, что поставленным требованиям критерия удовлетворяют параметры регулятора, найденные из уравнений вида

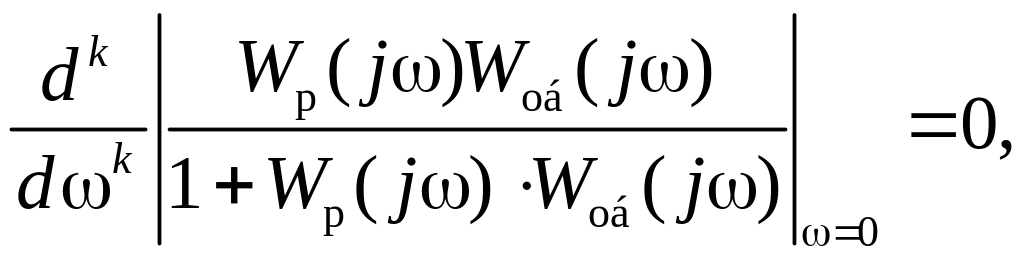. k = 1, 2,…2l. (2.20)

Этот критерий предназначен для расчета систем, которые должны как можно наиболее точно воспроизводить полезный сигнал.

Считается, что система управления, рассчитанная на основании (2.20), обеспечивает малое перерегулирование и малое время протекания переходных процессов.

k_п

2.5. Расчет параметров настройки регулятора на основании критерия максимальной степени устойчивости

Пусть объект управления описывается передаточной функцией вида

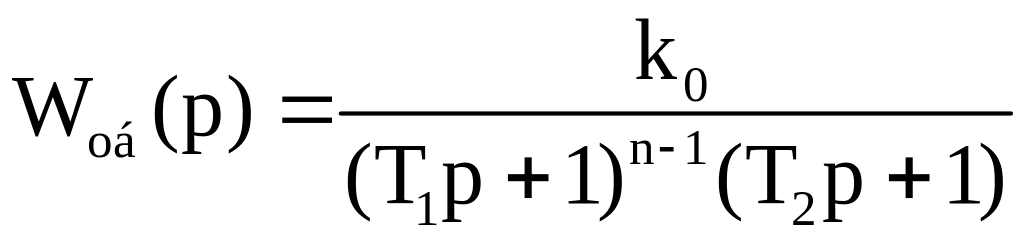, T₂ > 10T₁, T₂ / T₁ = q. (2.21)

Передаточной функцией такого вида можно аппроксимировать динамические характеристики многих промышленных процессов.

Используем наиболее полный типовой ПИД-регулятор для синтеза систем управления.

Оптимизируемыми являются параметры k_пр, k_и, k_д, при которых имеет место максимальная степень устойчивости

I =  min max Re (λ_i), (2.22)

где λ_i  корни характеристического полинома

(2.23)

который при замене λ на λ₁  I принимает вид

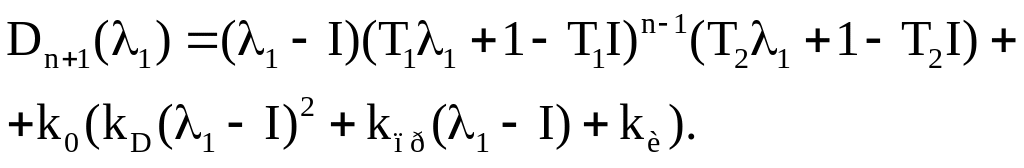(2.24)

В результате исследований Шубладзе, Черепова было установлено, что структура корней оптимального по степени устойчивости (2.22) зависит только от q и n. При этом для любого значения q существуют такие n_qi (i = 1,…,4), что при n < n_qi крайними правыми корнями (2.23) оптимального решения являются четыре кратных действительных корня, при n_q1 < n < n_q2  три кратных действительных корня и комплексно-сопряженная пара корней, при n_q2 < n < n_q3  два кратных действительных корня и комлексно-сопряженная пара корней.

Рассмотрим первый случай, когда n_q = 4, n_k = 0, n < n^*, где n* предельное значение n, для которого нарушается структура корней.

При обратной замене λ_i на λ + I можно переписать характеристический полином

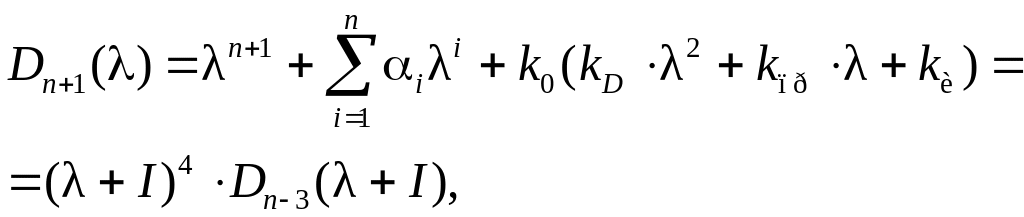(2.25)

в котором D_n3( + I) имеет корни левее прямой λ = I. Из (2.25) следует, что третья производная D_n+1() не зависит от параметров регулятора, поэтому крайний правый корень также не зависит от этих параметров. Значение этого корня и определяет степень устойчивости

maxRe λ_i = I, i =1,…, n  2, (2.26)

где λ_i  корни полинома

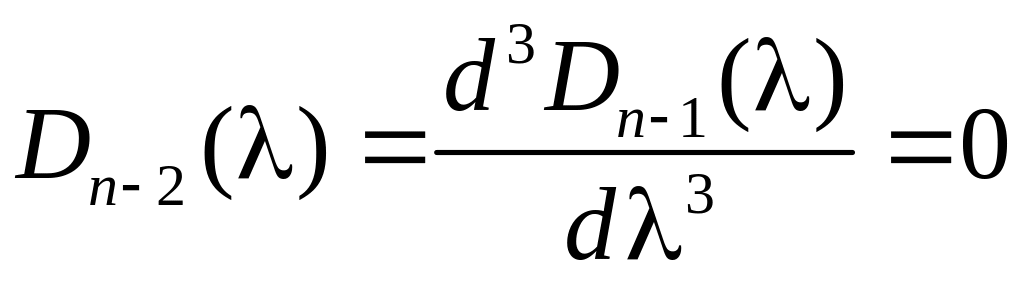. (2.27)

При известном значении I, уменьшая порядок дифференцирования, можно найти параметры настройки регулятора. Формулы для расчета I, k_пр, k_и, k_д имеют вид:

при n = 2;

, при n > 2;

;

;

; (2.28)

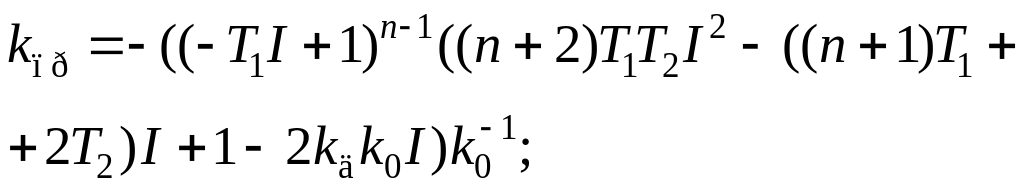
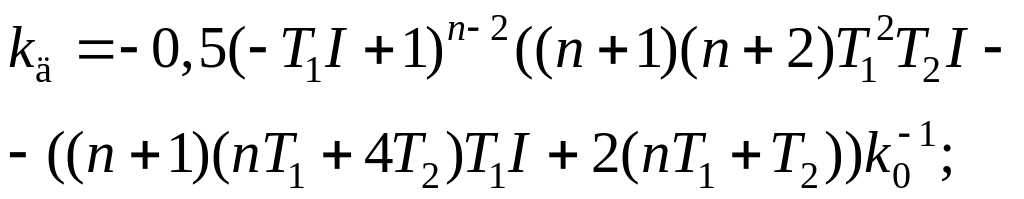
2.6. Метод синтеза пид-регулятора из условия обеспечения системой запаса по фазе и желаемого времени регулирования

Амплитудно-фазовая характеристика разомкнутой системы при частоте ω₁ проходит через точку e^{j(180 + φ}m⁾, где φ_m есть запас по фазе:

W_p(jω₁)W_oб(jω₁) = e^{j(180 + φ}m⁾. (2.29)

Если аргумент функции W_p(jω₁) обозначить через Θ, то

Θ = 180^ + φ_m  argW_об(jω₁). (2.30)

По модулю на частоте ω₁ имеем соотношение

|W_p(jω₁)| = |W_oб(jω₁)|^-1. (2.31)

С учетом выбранного закона регулирования перепишем (2.29) в виде

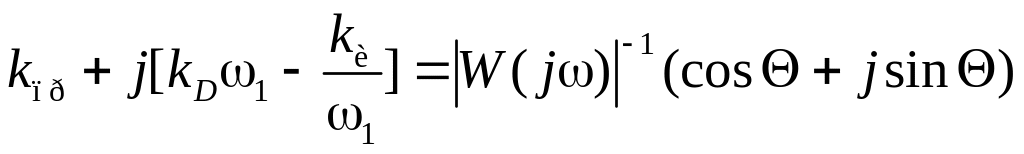. (2.32)

С учетом желаемого времени регулирования t_p можно определить приближенно (точно для систем второго порядка) частоту ω₁ на основании

ω₁ ≈ 8/(t_ptgφ_m). (2.33)

Из уравнения (2.32) составим два уравнения:

; (2.34)

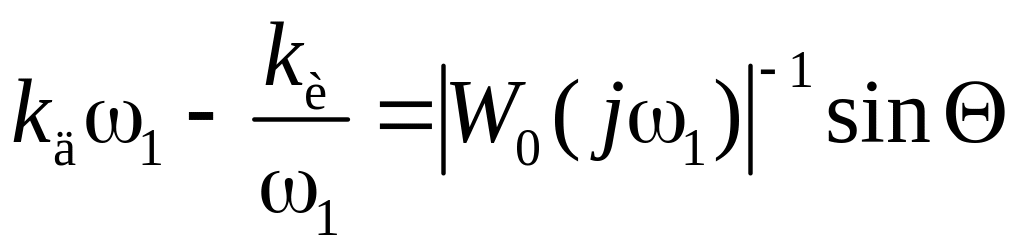. (2.35)

Для хорошо демпфированных систем запас по фазе составляет 3060^. Задаваясь значением φ_m, например φ_m = 45, находим из уравнения (2.33) ω₁ и из уравнения (2.34) коэффициент пропорциональности. На основании уравнения (2.35) находим соотношение для коэффициентов k_д, k_и. В этом случае можно задаться одним из коэффициентов, например, k_и. Если неудачно выбрать число k_и, например выбрать несколько увеличенное значение, то в систему вносится большее отставание по фазе. Это приводит к большему перерегулированию и более длительному переходному процессу. Поэтому можно снова задаться соотношением k_д k_и = (0,10,15). Если система позволяет ограничиться ПИ- или ПД-регуляторами, то тогда уравнения (2.34) и (2.35) позволяют найти однозначные значения параметров настройки регулятора.