Глава 2. Синтез линейных непрерывных систем управления

2.1. Общие положения систем управления

Иногда добиться желаемого качества системы можно путем настройки ее параметров. Однако часто этого оказывается недостаточно, и для получения желаемого результата необходимо изменить структуру системы автоматического управления. Поэтому под синтезом будем понимать способ выбора структуры системы и нахождение значений параметров настройки. Неизменяемую часть системы назовем объектом управления. А устройство, с помощью которого обеспечивается коррекция динамических характеристик системы, будем считать продуктом синтеза и называть регулятором или корректирующим элементом.

Для одноконтурной системы наиболее часто регулятор включается последовательно с объектом управления (рис. 2.1).

Рис. 2.1. Структура простейшей одноконтурной системы регулирования

Для многих одноконтурных систем можно выбрать регулятор на основе типовой структуры, отвечающий одному из следующих законов:

пропорциональный закон:

u(t) = k_пε(t); (2.1)

интегральный закон:

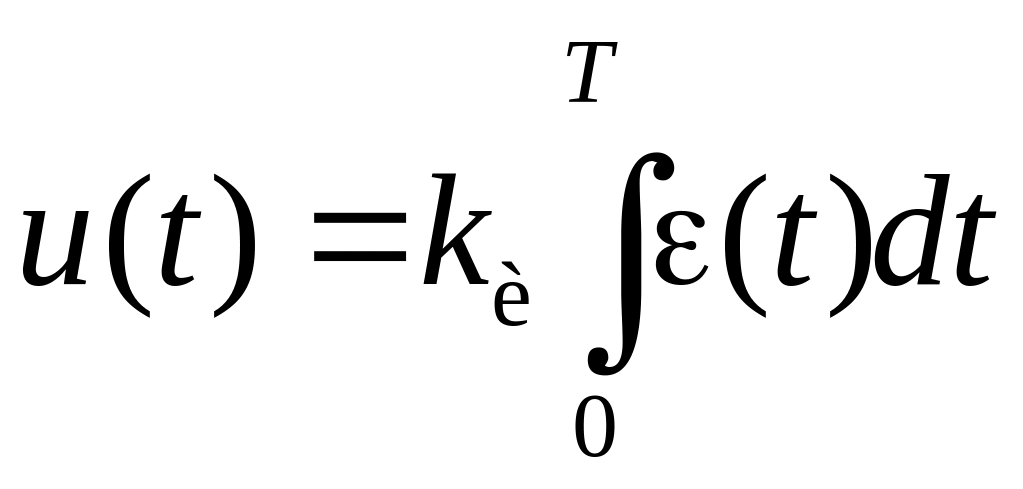; (2.2)

дифференциальный закон:

; (2.3)

пропорционально-интегральный закон:

u(t) = k_пε(t) + 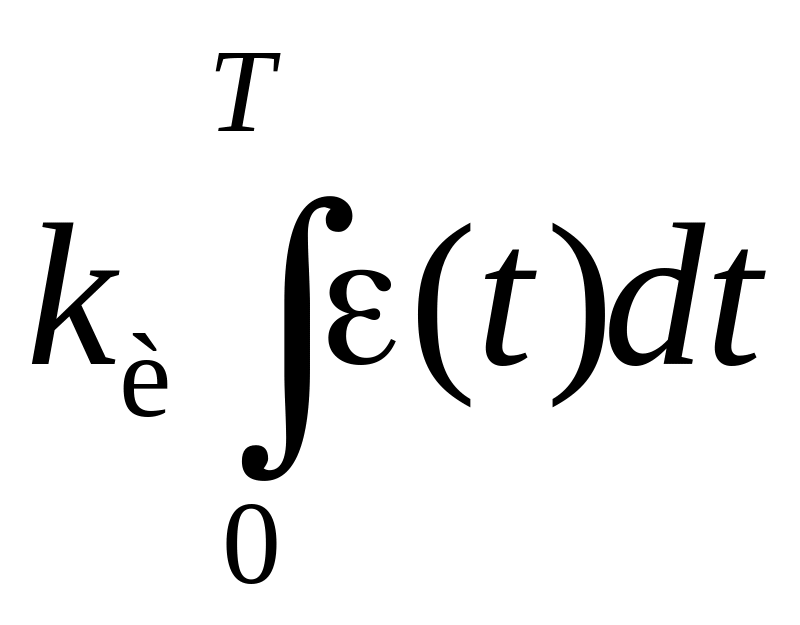; (2.4)

пропорционально-дифференциальный закон:

u(t) = k_пε(t) + ; (2.5)

пропорционально-интегрально-дифференциальный закон:

u(t) = k_пε(t) + + ; (2.6)

Пропорциональный регулятор обеспечивает высокое быстродействие, но для многих объектов сохраняется установившаяся ошибка. Интегральный регулятор позволяет исключить установившуюся ошибку, однако ухудшает устойчивость системы. Дифференциальный регулятор позволяет обеспечить ускорение динамических процессов в системе.

Система регулирования должна удовлетворять следующим основным требованиям:

а) с максимальной точностью обрабатывать задание g(t), при этом необходимо, чтобы система была хорошо управляемой, т. е. ее чувствительность (dy/dg) должна быть достаточно большой;

б) по возможности не реагировать на возмущения F(t), т. е. ошибка в системе под действием возмущения должна быть минимальной, а также необходимо, чтобы чувствительность системы (dy/dF) по данному каналу воздействия была слабой.

В зависимости от назначения системы на первый план выступает либо одно из двух вышеперечисленных требований, либо одновременно оба.

Первой проблемой, с которой сталкиваются при выборе регулятора, является выбор критерия качества.

При выборе критерия качества необходимо учитывать спектры входных сигналов. С точки зрения отработки системой, задающего воздействия, нужно иметь широкую полосу пропускания. С точки зрения подавления помех, возмущений, система должна иметь узкую полосу пропускания за пределами спектра возмущения.

2.2. Синтез одноконтурных систем автоматического управления исходя из условия обеспечения заданной степени затухания

Пусть из анализа существующей системы управления ориентировочно выбран регулятор, отвечающий одному из типовых законов.

При оценке качества систем управления на основе косвенных методов была получена зависимость степени ψ затухания от ближайшего к мнимой оси корня, связанного с параметром m:

. (2.7)

При m = 0 имеем границу области устойчивости. При расчетах промышленных систем регулирования чаще всего выбирают значение m от 0,22 (ψ = 0,75) до 0,366 (ψ = 0,9). Пусть в комплексной плоскости корней характеристического уравнения мнимая ось сдвинута до совпадения с корнем, местоположение которого характеризуется параметром m. Такому смещению мнимой оси соответствует подстановка частотной области

p = mω ± jω. (2.8)

Исходя из условия «попадания» одного из корней на мнимую ось можно в соответствии с критерием Найквиста записать

W_p(mω ± jω)∙W_oб(mω ± jω) = 1. (2.9)

Из уравнения (2.9) можно получить два уравнения:

A_pA_oб = 1; (2.10)

φ_p + φ_oб = 0, (2.11)

где A_p, A_oб  соответственно амплитудно-частотные характеристики и φ_p, φ_oб  фазочастотные характеристики регулятора и объекта.

Рассмотрим особенности расчета параметров настройки отдельных регуляторов. При условии расчета параметров настройки П-регулятора неизвестный коэффициент пропорциональности k_пр равен A_p. Нулевой сдвиг фазы пропорционального регулятора заменим на –π. Тогда уравнения (2.10), (2.11) примут вид:

k_пр∙ A_oб(mω ± jω) = 1; (2.12)

π + φ_oб(mω ± jω) = 0. (2.13)

Из уравнения (2.13) найдем частоты, а затем на основании уравнения (2.12) определим k_пр.

При расчете параметров настройки П-регулятора искомыми коэффициентами будут k_пр и коэффициент при интегральной составляющей k_и. Перепишем уравнение (2.10), (2.11) с учетом искомых коэффициентов k_пр и k_и:

A_p(m, ω, k_пр, k_и)∙A_oб(m, ω) = 1; (2.12)

φ_p(m, ω, k_пр, k_и) + φ_oб(m, ω) = 0. (2.13)

Для произвольно заданных значений ω < ω_гр можно найти множество значе­ний k_пр и k_и, которые будут обеспечивать желаемую степень затухания пере­ходного процесса. Граничную частоту ω_гр можно определить из условия:

A_oб(ω_гр) ≈ 0. (2.14)

Имея массив коэффициентов, можно ввести дополнительные критерии качества регулирования для нахождения лучшей пары k_{пр и} k_и. Ориентировочно можно выбирать значения из области параметров, k_пр , k_и стремится к максимуму.

При расчете параметров ПИД-регулятора тесно свяжем коэффициент при дифференцирующей составляющей k_Д с коэффициентом k_и:

k_и  k_D ≈ (0,1÷0,15).

Весь дальнейший расчет ПИД-регулятора аналогичен расчету для ранее рассмотренного ПИ-регулятора.

Пример расчета параметров настройки ПИ-регулятора для объекта

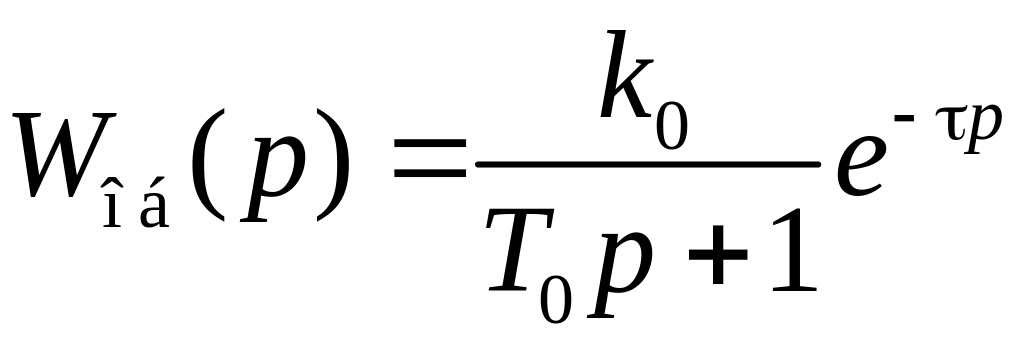. (2.15)

Расширенная амплитудно-частотная характеристика объекта имеет вид

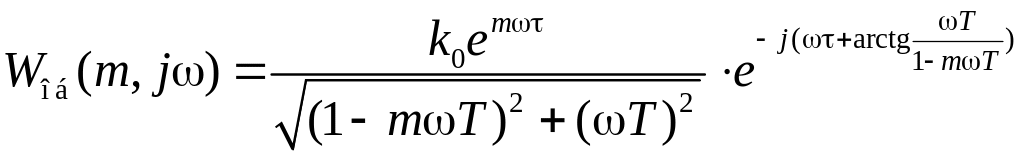. (2.16)

Для выбранной структуры ПИ-регулятора расширенная амплитудно-фазовая характеристика (АФХ)

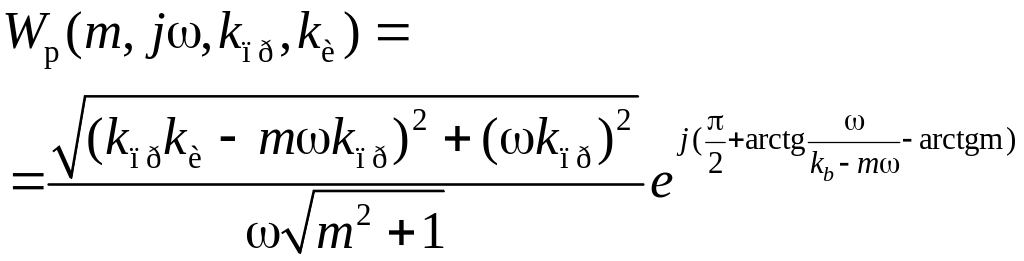(2.17)

Пусть для объекта с параметрами T₀ = 14,2, k₀ = 14,7, τ = 3,5 желаемая степень затухания ψ = 0,75. Подставляя значения расширенных АФХ объекта и регулятора в уравнения (2.12),(2.13) для частот в диапазоне 0,10,4, находим численные значения, которые сведены в табл. 2.1.

Таблица 2.1

ω	0,1	0,2	0,3	0,4
kпр kи	0,0087	0,029	0,036	0,014
kпр	0,01	0,12	0,23	0,29