38. Системы случайных величин, их закон распределения
Системой случайных величин (случайным вектором, многомерной случайной величиной) называется любая упорядоченная совокупность случайных величин Х ={X1, …, Xn}. Случайные величины{X1, …, Xn}, входящие в систему могут быть как непрерывными, так и дискретными.
Двухмерная случайная величина (Х,У) является дискретной, если множества значений ее компонент X={x1, …, xn} и Y={y1, …, ym} представляют собой счетные множества.
pij = P(X =xi , Y = yj ) ,i=1..n , j=1..m.
Матрица распределения системы двух случайных величин записывается в виде:
Сумма всех вероятностей pij, стоящих в матрице распределения вероятностей равна единице как сумма вероятностей полной группы событий:
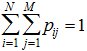
Зная
матрицу распределения системы двух
дискретных случайных величин (X,Y), можно
найти закон распределения отдельных
случайных величин, входящих в систему:
39. Свойства закона распределения двумерной дискретной с.в.
Св-ва закона распределения: pij>=0; условия нормировки: Σ pij=1; pij, pij – маржинальне вероятности; Σjpij= pi или Σipij= pj
42. Свойства коэффициента корреляции
Коэффициента корелляции называется число:
ч=ч(x,y)= К xy/Gx Gy ,kxy=Mxy-MxMy
Свойства корелляции:
y
a˃0
x
1)|ч|≤ 1
2) ч = 1 корелляция положительна и линейная, y=аx+b
меры линейности случайных величин
3) ч = -1 отрицательная корелляция (а˂0)
ч = аx-b связь линейна
y
(а˂0)
x
4) Если случайные величины x и y независимы, то коэффициент корелляции равен 0, ч=0
Вывод: Если на практике при вычислении коэффициента корелляции получается число ч≈1, то связь получается линейная, если число близко к 0, то связь будет нелинейной или отсутствует вообще.
43.Цели и задачи математической статистики. Понятие выборки и ее свойства Мат.статистика-наука, которая изучает методы сбора ,обработки различных результатов наблюдений, а так же прогнозирование и определение законов распределения. Задачи:1.Сбор и первичная обработка наблюдаемых значений;2.Оценка основных характеристик требуемых по исследованию (Например :Мх ;Дх);3.Проверка статистических гипотез. Выборочной совокупностью(выборкой)называется часть объектов отобранных случайным образом из генеральной совокупности. Выборка должна обладать свойствами репрезентативности. Генеральная совокупность-совокупность всех значений СВ(случайной величины)подвергшихся изучению.
N – число объектов ген.совокупности
n – число объектов выборки
Репрезентативность – свойство выборки воспроизводить характеристики генеральной совокупности. Одна и та же выборка может быть репрезентативной и нерепрезентативной для разных генеральных совокупностей.
Выборки бывают:Повторные?Безповторные?Простая ?Типическая?Механическая?Серийная
Пр:2;4;5;9;
44.Нахождение закона распределения дискретной случайной величины по его выборке.
Пусть наблюдается дискретная СВ на которой производят некоторый эксперимент и сделав замеры получают Х1,х2,х3…хn где n-число появлений варианта. n1+n2+n2+…+nk=n Pi*=ni/n –относительная частота появления варианта.(частости) тогда законом распределения дискретной СВ будет:
хi |
X1 |
… |
xn |
ni |
N1 |
… |
nk |
хi |
X1 |
… |
xn |
Ni/n |
N1/n |
… |
Nk/n |
45. Эмпирическая функция распределения ее свойства. Пусть наблюдается непрерывная СВ над которой производят некоторый эксперимент и сделав замеры получают (х0;х1)(х1;х2)…(хk-1 ;xk) где х0=х начальное х0=х1-h/2 h-шаг хmax-xmin размах выборки h= (xmax - xmin) /(1+log2n)= (xmax - xmin)/(1+3.22lgn)
Вариационный ряд можно представить с помощью эмперической функции распределения
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения x относительную частоту события
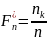
где nx – число вариант, меньших x; n – объем выборки.