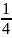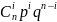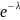12.Теорема Байеса.

Если в результате испытания событие A, вероятность которого была вычислена по формуле полной вероятности, наступило, то вероятности гипотез можно переоценить по формуле Байеса:

Р(Нi/А)= .

ВероятностиР(Hi) называют априорными, а вероятности Р(Hi/А)− апостериорными вероятностями гипотез.

Пример: Группа из 12 стрелков включает в себя трёх мастеров спорта, четырёх кандидатов в мастера и пятерых перворазрядников. Мастер спорта может попасть в мишень с вероятностью 0,9, кандидат в мастера – с вероятностью 0,85, перворазрядник – с вероятностью 0,75. Наудачу выбранный стрелок сделал выстрел, мишень была поражена (событие A). Какова вероятность того, что этот стрелок является мастером спорта?

Неизвестно, какой стрелок сделал выстрел. Имеются гипотезы: H1 – стрелял мастер спорта, H2 – стрелял кандидат в мастера, H3 – стрелял перворазрядник. По условию, P(H1)=3/12, P(H2)=4/12, P(H3)=5/12. Кроме того, даны вероятности попадания для стрелков каждой группы: P(A/H1)=0,9, P(A/H2)=0,85, P(A/H3)=0,75. Таким образом,

P(A)=P(A/H1)P(H1) + P(A/H2)P(H2) + P(A/H3)P(H3) = (0, 9⋅3+0, 85⋅4 + 0, 75⋅5)/12 ≈ 0,821.

Тогда, по формуле Р(Нi/А)= = =0,274

13.Понятие схемы Бернулли. Формула Бернулли.

Предположим, что проводятся независимые испытания и в каждом из них может наступить два исхода – успех с вероятностью р или неудача с вероятностью q (p+q=1). Такую последовательность испытаний называют схемой Бернулли.

Эксперимент с 2-мя исходами называется экспериментом типа Бернулли.

А – событие произошло Р(А)=р

– событие не произошло р( )=1-Р(А)=1-р=q

p+q=1 k={0,1,2…n}

- вероятность появления события ровно k раз при n независимых испытаниях, p - вероятность появления события при одном испытании.

Пр. Вероятность нормального приживления саженца плодового дерева p = 0,8. Найти вероятности, что:

1) из 10 саженцев приживется ровно 8;

Решение.

1. Ясно, что приживления отдельных саженцев можно считать независимыми, поэтому ситуация соответствует схеме Бернулли. Тогда по формуле Бернулли получаем

14.Наивероятнейшее число появления события А в схеме Бернулли.

Число k0, при котором вероятность появления события А в п независимых испытаниях постоянна и =р, называется наивероятнейшим числом.

np−q≤k0< np+p,

Св-ва k0:

[np+p]-[np-q]=np+p-np+q=p+q=1

[np+p], целое, то [np-q]- целое

Если [np-q] – дробное, то [np+p] тоже дробное

Пр. n=10 p=1/2 q=1/2

Найти наивероятнейшее число выпадений герба

10*1/2-1/2≤ k0≤10*1/2+1/2 4,5≤ k0≤5,5 k0=5

15.Следствие из локальной теоремы Муавра-Лапласа. Пример. Свойства функции Гаусса.

Пусть событие А может произойти в любом из n повторных независимых испытаний с постоянной вероятностью р отличной от 0 и 1. пусть событие А не редкое, а количество испытаний достаточно велико, т.е. выполняются условия Муавра-Лапласа:n≥100,npq≥20 тогда справедлива локальная формула Муавра-Лапласа.

- вероятность появления события ровно k раз при n независимых испытаниях,

p - вероятность появления события при одном испытании, q =1− p .

= - функция Гаусса

Свойства : 1)затабулирована 2)четная 3)быстро стремится к 0. при х≥4

Пример: Вероятность того, что посеянное семя взойдет равна 0,85. найти вероятность того, что ровно 213 из 250 семян взойдет.

Решение: n = 250 > 100; k = 213; p = 0,85; q = 0,15;

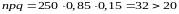
16.Теорема Пуассона. Пример.

Пусть количество испытаний n достаточно велико, а вероятность р мала, т.е. выполняются условия Пуассона:n≥100,λ≤10, тогда справедлива формула Пуассона

Если число экспериментов достаточно велико, а вероятность появления события А постоянно стремится к 0, то вероятность того, что наступит k раз:

,

Пример: Вероятность изготовления стандартной детали равна 0,995. Найти вероятность того, что среди 1000 деталей будет более 3-х браков.

Решение: n = 1000 ≥ 100 ; k > 3; p = 0,005; q = 0,995;

λ=n*p=1000*0,005=5<10

17. Интегральная теорема МУАВРА-ЛАПЛАСА. СВОЙСТВА ФУНКЦИИ Ф(Х). ПРИМЕР

Пусть событие А может произойти в любом из n повторных независимых испытаниях с постоянной вероятностью р отличной от 0 и 1. Пусть количество испытаний велико, а события не редкие, т. е. выполняются условия Муавра-Лапласа. Тогда вероятность того, что количество успехов заключено в некотором интервале определяется интегральной функцией Муавра-Лапласа.

,

Ф(х)=

Св-ва:

1. затабулирована

2. Нечетная Ф(-х)=-Ф(х)

3. при х≥5, Ф(х)≈0,5

П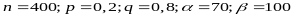 р: Вероятность того, что деталь не пройдет контроль равна 0,2. Найти вероятность того, что среди 400 деталей число не прошедших контроль заключено в пределах от 70 до 100.

Применим формулу 3 и подставим полученные данные.

18.Понятие случайной величины. Основные типы случайных величин. Пример.

Случайная величина – числовая величина, которая принимает те или иные значения, в зависимости от случая.

Случайная величина:

• Дискретная – случ. велич., которая принимает конечное или счетное число значений.

• непрерывная – случ. велич., значение которой сплошь заполняет определенный числовой промежуток.

• смешанная – случ. велич., которая не является ни дискретной, ни непрерывной.

Примеры:

бросание монеты: А – герб; В – решка;

выстрел из ружья или пистолета: А – попадание; В – промах;

19.Закон распределения дискретной с.в. Полигон.

Для того, чтобы задать дискретную случ. велич., нужно знать значения, которые принимает величина х1,х2… и вероятности с которыми эти значения принимаются: рi=Р( )

Множество пар (xi, pi) составляют закон распределения дискретной случайной величины.

	x1	x2	…	xn
pi	p1	p2	…	pn

- закон распределения

Полегоном называется ломаная линия, содиняющая точки с координатами (xi, pi).

Пр: монета брошена 2 раза. Случ. велич. определяет выпадение герба. Составить закон распределения случ. велич и построить полегон.

	0	1	2
pi

Р1=Р( =0)= = Р2=Р( =1)= = Р3=Р( =2)= =

Рконтр= + =1

Построим полигон

20.Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной с.в.

Математическим ожиданием дискретной случ. велич. называется число, которое = сумме произведений значений случайной величины на соответствующие вероятности, т.е.:

- ряд должен быть абсолютно сходящимся.

Если ряд расходится или сходится условно, то мат. ожид. не существует.

Свойства математического ожидания.

1)М(С)=С 2)М(С*X)=C*M(X) 3)M(X±Y)=M(X)±M(Y)

4)если X и Y – независимые случайные величины,то M(X*Y)=M(X)*M(Y)

Дисперсия определяет разброс значений случ. велич вокруг математического ожидания

Дисперсия – число неотрицательное.

Свойства дисперсии.

D(X)≥0

D(C)=0

D(C*X)=C²*D(X)

если X и Y – независимые случайные величины,то D(X±Y)=D(X)+D(Y)

Среднее квадратическое отклонение.

характеризует средний разброс в тех же единицах, что и сама случайная величина.Число неотрицательное

Пример № 1:

	0	1	2
	0,04	0,32	0,64

21. Начальные и центральные моменты дискретной с.в.

Начальным моментом порядка K случайной величины Х называется математическое ожидание величины ХK:

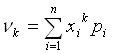
V0=1

V1=M(Х)

Центральным моментом порядка K случайной величины Х называется математическое ожидание K-Й степени отклонения:

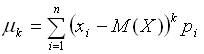
μ 0=1

μ1 = 0

μ 2= D(X)

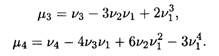
22. Бернулевская с.в., ее математическое ожидание и дисперсия.

Дискретная случайная величина – бернулиевская с параметрами (n,р), если она принимает значения от 1до n с вероятностями, кот. вычисляются по формуле Бернули p(k)=(ξ=k) = C_n ^k p^k q^n-k

	0	1	…	i	…	n-1	n
pi	qn	npqn-1	…		…	np n-1q	pn

Mξ = np

Dξ = npq

23. Пуассоновская с.в., ее математическое ожидание и дисперсия

Дискретная случайная величина - пуассоновская с параметром λ, если она принимает значения бесконечное, но счетное множество значений с вероятностями

P(k) = P (ξ=k) = λ^k/k! *e^-λ

λ=np

Mξ = λ

Dξ = λ

	0	1	2
pi

25. Закон распределения непрерывной с.в. Его свойства.

Случайная величина, возможные значения которой непрерывно заполняют некоторый промежуток, называется непрерывной случайной величиной.

Функция распределения F(x) определяет вероятность того, что случайная величина примет значение меньше, чем фиксированное x.

1. F(+∞)=1 1

F(-∞)=0 0

F(x)=[0,1]

2. F(x0)- непрерывна слева

3. F(x)- неубывающая

Если х1<x2, то F(x1) F(x2)

4) P(x1 ξ < x2) = F(x2) − F(x1) – вероятность попадания величины в заданном интервале

5) F(x) непрерывна в т.x0 или вблизи её, то P(ξ=x0)=0

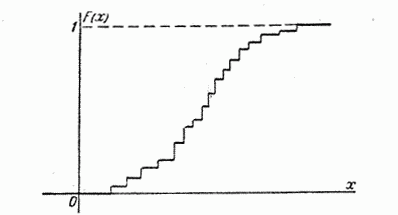
Графически функция распределения выглядит следующим образом:

Свойства:

1.P(x1

2.Функция распределения является универсальной

Пример. Случайная величина Х задана таблицей распределения:

 

Х	- 1	2	3	5
Р	0,1	0,3	0,4	0,2

 

Составить функцию распределения F(x) случайной величины Х и построить ее график.

Решение. Если х-1, то F(x)=P(X<x)=0;

если –1<x2, то F(x)=P(X<x)=P(X=-1)=0;

если 2<х3, то F(x)=P(X=-1)+P(X=2)=0,1+0,3=0,4;

если 3<x5, то F(x)=P(X=-1)+P(X=2)+P(X=3)=0,1+0,3+0,4=0,8;

если х>5, то F(x)=P(X=-1)+P(X=2)+P(X=3)+ Р(Х=5)=1

Построим график.

Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) – F(a) = 0. Поэтому для такой случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал. Вторым способом задания закона распределения непрерывной случайной величины является так называемая плотность распределения (плотность вероятности, дифферен-циальная функция). Случайная величина называется непрерывной, если она может принимать любые значения внутри определенного интервала, который иногда имеет резко выраженные границы, а иногда – нет. К непрерывным случайным величинам относятся, например, масса тела и рост взрослых людей, масса тела и объем мозга. составить таблицу, в которой были бы перечислены все ее возможные значения, или построить многоугольник распределения нельзя. Кроме того, вероятность какого-либо ее конкретного значения очень мала (близка к 0). Закон распределения вероятностей такой величины должен позволить найти вероятность попадания ее значения в любой заданный интервал (х1, х2), лежащий внутри (а,b).

26. Вероятность попадания непрерывной с.в. в заданный интервал, выраженная через функцию распределения

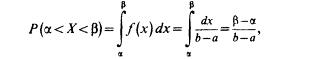- равномерная

P(α<ξ<β)=e^-αλ - e^-βλ- показательная

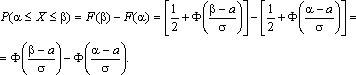- нормальная

27. Функция распределения дискретной с.в

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:

Свойства интегральной функции распределения:

1.

2.

3.

4.

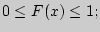
5. непрерывна слева

6. она непрерывна в точке Х0 или вблизи нее, если P (ξ=Х0)=0

7. она является универсальной

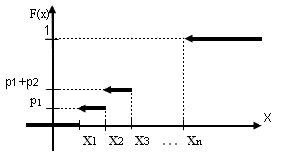
Если закон распределения дискретной случайной величины Х задан в виде таблицы:

x	x1	x2	х3	…	хn
p	р1	р2	р3	...	рn

то функция распределения F(x) определяется формулой:

0 при х≤ x_1,

р₁ при x₁< х≤ x_2,

F(x)= р₁ + р₂ при x₂< х≤ х₃

… … …

1 при х> х_n.

29. Числовые характеристики непрерывной с.в

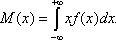
Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум(F(x) принимает макс значение). Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным.

Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Нач.момент

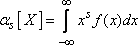
центральный момент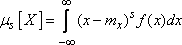

31. теоремы о математическом ожидании

Математическое ожидание постоянной величины равно самой постоянной: М(С) = С.

Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(Х).

Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий сомножителей

M(XY) = M(X)·M(Y).

Математическое ожидание суммы (разности) двух случайных величин равно сумме их математических ожиданий слагаемых. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий слагаемых.

M(X+Y) = M(X) + M(Y); M(X-Y) = M(X)-M(Y)

32. теоремы о дисперсии

Дисперсия ровна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:

D(Х)= М(Х²)-( М(Х))²

Дисперсия постоянной величины равна нулю: D (С)=0

Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)=C2 ·D(X).

Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D (X + Y) = D (X) + D (У)

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D (X — Y) = D (X) + D (У)

33. Равномерно распределенная с.в. Ее плотность и функция распределения. Вероятность попадания в заданный интервал

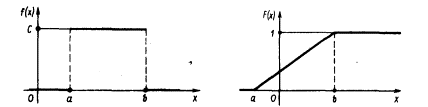
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность имеет следующий вид:

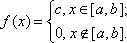
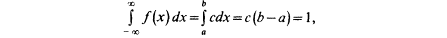откуда с=1/(b-a).

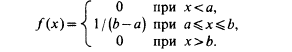
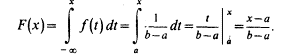
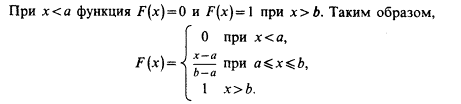
Графики функций f(x) и F(x) имеют вид:

34. Математическое ожидание и дисперсия равномерно распределенной с.в.

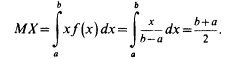
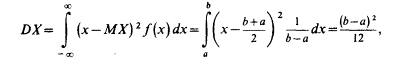
35. Показательно распределенная с.в., ее математическое ожидание и дисперсия

Непрерывная случайная величина Х, функция плотности которой задается выражением

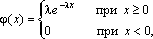
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Здесь параметр λ постоянная положительная величина.

Математическое ожидание = 1 / λ

Стандартное отклонение = 1 / λ

Дисперсия = 1 / λ2

P(α<ξ<β)=e^-αλ-e^-βλ

36. Нормально распределенная с.в., ее закон распределения, математическое ожидание и дисперсия

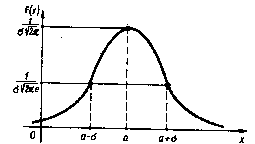
Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид

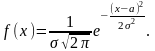
где а—некоторые постоянные, называемые параметрами нормального распределения.

Св-ва функции f(x):

1. Областью определения функции f(x) является вся числовая ось.

2°. Функция f{x) может принимать только положительные значения, т. е. f(x}>0.

3°. Предел функции f(x) при неограниченном возрастании |х| равен нулю, т. е. ось ОХ является горизонтальной асимптотой графика функции.

4°. Функция f{x) имеет в точке х = a максимум, равный

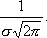
5°. График функции f(x) симметричен относительно прямой х = а.

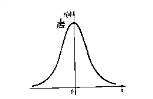
Функция плотности нормального распределения f(x) с параметрами а=0, s =1 называется плотностью стандартной нормальной случайной величины и ее график имеет вид:

37. Вероятность попадания нормальной с.в. в заданный интервал

P( =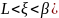

найдем вероятность того, что модуль отклонения нормального распределения величины Х от ее центра распределения а меньше 3σ. Имеем

Р(|x – a| < 3 s) =P(а–3 s< X< а+3 s)= Ф(3) – Ф(–3) = 2Ф(3) »0,9973. Значение Ф(3) получено по таблице функции Лапласа.

Принято считать событие практически достоверным, если его вероятность близка к единице, и практически невозможным, если его вероятность близка к нулю. Мы получили так называемое правило трех сигм: хотя нормальная случайная величина распределена на всей оси х, интервал ее практически возможных значений есть (a–3σ, a+3σ).