1.Понятие случайного эксперимента, множества его исходов. Примеры.

Под экспериментом понимают выполнение некоторого комплекса условий. Например, стрельба из лука, подбрасывание монеты.

Каждому эксперименту можно поставить в соответствие множество элементарных исходов.

Множество всех исходов, соответствующих эксперименту, образует пространство элементарных исходов. Его обозначают Ω. Ω= {ω1, ω2…ω } где ω−элементарные исходы

Случайным експериментом называется испытание, исход которого нельзя предугадать, или говорят экс-перимент с двумя и более исходами. (Подбрасывание игрального кубика.)

2.Понятие события. Равенство, сумма событий и ее свойства.

Событием называется подмножество пространства элементарных исходов.

Эксперимент– игра в шахматы. Событие– выигрыш, ничейный исход или проигрыш

События обозначаются большими буквами латинского или греческого алфавита А, В, С

Равенство А=В События называются равновозможными, если по условию эксперимента нет оснований считать одно более возможным, чем любое другое.

Пример В урне10 одинаковых шаров: 5 белых и5 черных. Нау-дачу извлекается шар. Здесь события«появится белый шар» и«появится черный шар» равновозможны.

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них,либо оьа вместе в результате испытания

Турист хочет и имеет возможность посетить2 города. Обозначим события: А= {турист посетил город А}, В= {турист посетил го-род В}. Событие А+В заключается в том, что турист посетил только один из городов А и В или он посетил их оба.

Свойства: 1)А+В=В+А 2)(А+В)+С=А+(В+С) 3)А+А=А 4)А+Ø=А 5)А+Ω=Ω

3.Понятие события. Произведение и разность событий, их свойства. Понятие несовместности событий и разбиения.

Событием называется подмножество пространства элементарных исходов.

Эксперимент– игра в шахматы. Событие– выигрыш, ничейный исход или проигрыш

События обозначаются большими буквами латинского или греческого алфавита А, В, С

Произведением нескольких событий называетсясобытие, состоящее в совместном наступлении всех этих событий в результате испытания.

Пусть имеются следующие события: А = {из колоды

карт вынута дама}, В ={из колоды карт вынута карта бубновой масти}. Оче-видно, AB ⋅ есть событие{вынута дама бубновой масти}

Свойства: 1)АВ=ВА 2)(АВ)С=А(ВС) 3)АА=А 4)АØ=Ø 5)АΩ=А 6)А(В+С)=АВ+АС

Разностью событий А и В называется событие, в котором в результате испытания наступает событие А, но не наступает собы-тие В.(С=А-В)

События А и В называются несовместными, если их произведение есть невозможное событие АВ=∅.

СобытияH1, H2,…Hn образуют полную группу событий (или разбиение пространства Ω), если они попарно несовместны и в сумме дают все пространство элементарных исходов, то есть

1) Hi+Hj =∅; 2) ∑Hi= Ω.

Пример1.14. Стрелок произвел выстрел по мишени. Обязательно произойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.

4.Противоположные события, их свойства.

Событие 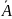=Ω−А называется противоположным событием к событию А (или дополнением)

Свойства 1. А ⋅ =∅  2. А+ =Ω.

Пример.Стрелок стреляет в мешень А={попадет в цель}, ={не попадет в цель}

5.Статистическое определение вероятности события. Ее свойства.

Пусть есть эксперимент Ω, в результате которого наступает событиеА. Под относительной частотой появления события А будем понимать p *( A)=k(A)/n, n− число повторений эксперимента, k (A) − число появления события А.

Если существует коненый предел относительной частоты появлений события А

lim p *( A)= p ( A) - статистическая вероятность.

n →∞

Пример. Вероятность выпадения герба р(Г)=1/2,решки – р(Р)=1/2

Свойства 1) p*(∅)=0 2)р*(Ω)=1 3)р*(А)=[0;1]

6.Классическое определение вероятности, ее свойства.

Вероятностью Р (А) появления события A называется отношение числа исходов,благоприятствующих наступлению этого события, к общему числу всех равновозможных исходов испытания Р (А) = ,где m− число благоприятствующих событию А исходов, а n−число всех исходов испытания.

Cвойства: 1)Р(Ø)=0 2)Р(Ω)=1 3)для любого АсΩ Р(А)є[0;1]

Пример Какова вероятность появления нечетного числа очков при одном бросании игральной кости?

Решение. Обозначим А= {выпадение нечетного числа очков}. Благоприятствующими исходами будут цифры { 1, 3, 5 } m= 3, ко всем исходам относятся цифры { 1, 2, 3, 4, 5, 6 }, n=6. Тогда искомая вероятность

P (A)= m/ n=1/3

7.Теорема сложения и следствия из нее.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: P (A+В)=Р(А)+(В)-Р(АВ)

Доказательство Р(А+В)= , = P (A+В)=Р(А)+(В)-Р(АВ),что т.д

Пример. В электрическую цепь последовательно включены две лампочки. Вероятность того, что лампочки перегорят, если напряжение в сети превысит номинальное, соответственно равны0,4 и0,7. Найти вероятность того, что при повышенном напряжении тока в цепи не будет.

Решение. Событие{тока в цепи не будет} является суммой событий A= {перегорит первая лампочка}, B= {перегорит вторая лампочка},так как события А и В совместны ,то без события АВ={перегорят две лампочки}.

Р(А+В)=0,4+0,7-0,4*0,7=0,82

Следствия: 1)Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС) 2)Если события А и В несовместны(А+В)≠Ø,то Р(А+В)=Р(А)+Р(В) 3)Р(А)=1-Р(Ā)