Подпространства

Рассмотрим линейную комбинацию векторов

= + +… (1)

Множество всех векторов вида (1) называется подпространством пространства , порожденным векторами , Среди векторов, образующих подпространство имеется (получается при ). Если система векторов линейно независимая, очевидно, что любые векторы, выделенные из этой системы также линейно независимы.

Предположим, что система векторов линейно зависима, т.е., например, есть линейная комбинация остальных

= + +…+ = , подставляем в (1) получим

= + = + =

Следовательно, каждый вектор (1) представляется в виде линейной комбинации векторов , ,… т.е. подпространство, порождаемое векторами , , , совпадает с подпространством, порождаемым векторами

, ,… . Следовательно, не изменяя подпространства, можно исключить из системы порождающих его векторов всякий вектор, являющийся линейной комбинацией. Производя последовательно такое исключение можно добиться, чтобы из заданной системы , остались только линейно-независимые, порождающие то же подпространство . Таким образом, при определении подпространства можно всегда считать, что порождающие его вектора линейно независимы. Одно и тоже подпространство может порождаться различными системами линейно независимых векторов. Однако справедлива следующая теорема:

Число линейно-независимых векторов, порождающих заданное пространство, при любом их выборе – одно и тоже.

Равномерностью подпространства называется число порождающих его линейно независимых векторов, порождающих векторов данное подпространство, называется его базисом. Данное понятие аналогичным образом можно обобщить и не пространство.

Критерий совместности систем линейных уравнений

Результаты полученные в векторной алгебре позволяют глубже исследовать системы линейных уравнений.

Рассмотрим систему

(в общем случае )

Обозначим через А матрицу из коэффициентов системы, а через - матрицу, полученную из А присоединением столбца свободных членов. Далее обозначив через столбцы матрицы системы, через - столбец свободных членов. Система (1) равносильна векторному уравнению

Введем понятие ранга матрицы. Под рангом матрицы понимается ранг системы векторов, образующих ее столбцы. Можно показать, что ранг системы векторов-столбцов всегда равен рангу систем векторов-строк. Другими словами ранг матрицы равен числу линейно-независимых столбцов (строк) через которые можно выразить остальные столбцы (строки) системы.

Ранг матрицы является одной из важнейших ее характеристик. Поэтому необходимо знать простые способы вычисления ранга. Одним из таких способов является метод Гаусса. Он основан на элементарных преобразованиях матриц. Под элементарными преобразованиями мы понимаем:

1. вычеркивание нулевой строки (столбца)

2. прибавление к одному из строк другой строки, умноженной на любое число

3. перестановка строк (столбцов)

Идея метода заключается в том, что с помощью элементарных преобразований заданная матрица приводится к виду

В котором все «диагональные» элементы отличны от 0, а элементы, расположенные ниже «диагонали» равны нулю. Справедлива следующая теорема: Ранг матрицы не меняется при элементарных преобразованиях.

Рассмотрим систему вектор строк ступенчатой матрицы

Рассмотрим вектор , являющийся линейной комбинацией векторов(*)

= + +…

Предположим, что . Первая координата есть если она равна 0, то (т.к. ), тогда вторая координата есть если и она равна 0 то ввиду и т.д. в итоге получим: только в случае это означает, что система вектор-строк ступенчатой матрицы равна rang (А)=r.

Для приведения матрицы к ступенчатому виду будем использовать ранее рассмотренное правило прямоугольников.

Пример: найти ранг матрицы

Прежде всего условимся, что если в процессе элементарных преобразований появляется нулевая строка то она сразу отбрасывается. Таким образом, в любой из оставшихся строк имеется хотя бы один не нулевой элемент который можно с помощью перестановки столбцов вывести на «диагональ».

 

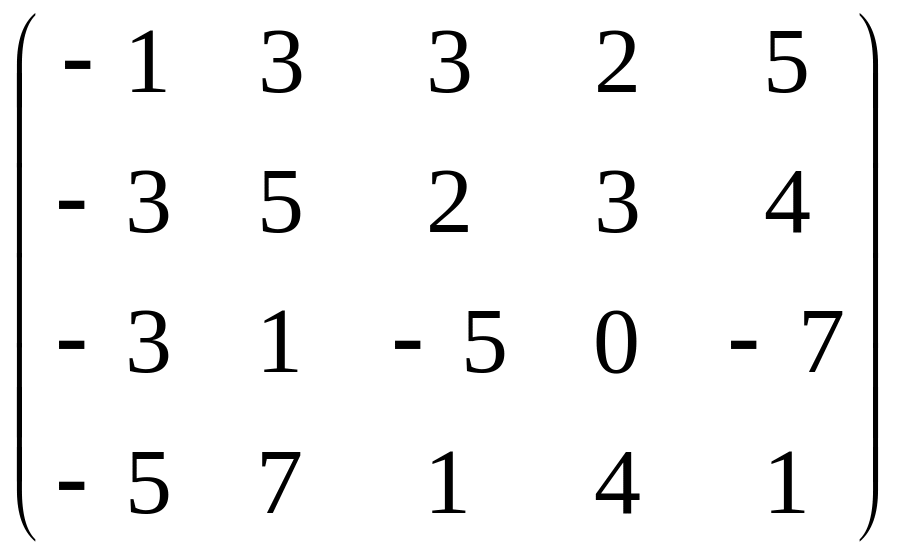
Вычеркиваем 3-ю строку. 3-й элемент в последней строке равен нулю, поэтому переставим местами 3-ю и 5-ю строку. Получим ступенчатую матрицу.

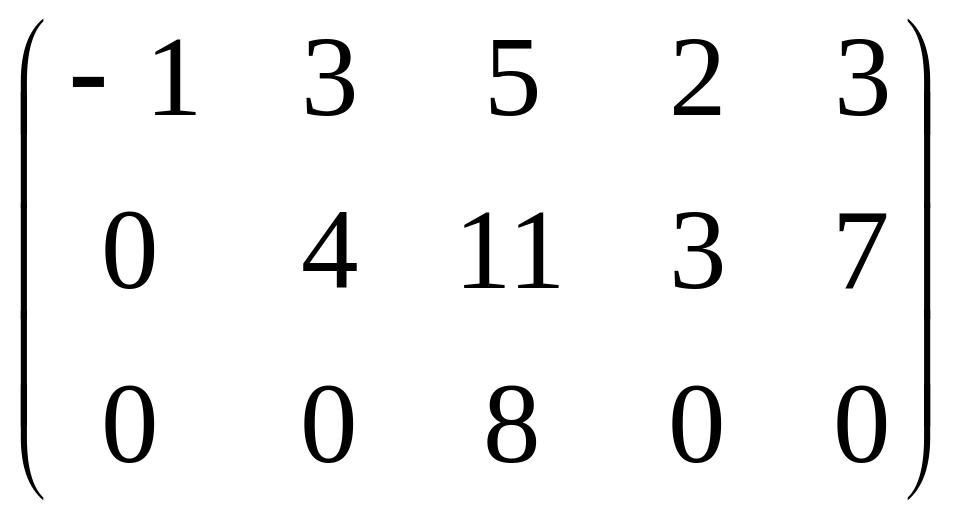
Ранг полученной матрицы равен 3 следовательно и ранг исходной матрицы равен 3.