2. Особенности моделирования экономических процессов методом непрерывных цепей маркова

Теперь, будем исходить из того, что в системе S потоки событий - простейшие, т.е. переход системы из состояния S_i^(k) в состояние S_j^(k) осуществляется с интенсивностью (см. рис. 3.)

при i  j (22)

где , 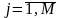- индексы обозначающие число состояний системы.

Рисунок 3. – Граф-процесса состояний системы

Обозначим S_к – интересующее нас состояние системы, в котором она находиться с вероятностью p_к(t) на любой момент времени. Вероятность нахождения системы в состоянии S_к на момент времени t+dt определим как произведение вероятности нахождения системы в любом состоянии S_i на момент времени t при i  k на условную вероятность того, что система за время dt из состояния S_i перешла в интересующее нас состояние S_к с вероятностью (см. рис. 3.3):

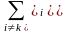(23)

где P_i(t) - вероятность нахождения системы в любом состоянии S_i;

- условная вероятность.

Или вероятность нахождения системы в состоянии S_к на момент времени t+dt определим как произведение вероятности нахождения системы на момент времени t в состоянии S_k на условную вероятность того, что система за время 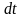, не ушла ни в какое другое состояние с вероятностью:

(24)

где P_k(t) - вероятность нахождения системы в состоянии S_к;

- условная вероятность.

Применяя правило сложения вероятностей, получим:

(25)

Раскрыв скобки, перенеся P_k(t) в левую часть, и разделив обе части уравнения на , устремив к нулю и перейдя к пределу, мы получим определение дифференциала⁴:

(26)

Решением СДУ является семейство кривых P_k(t), поэтому интегрирование этой системы уравнений даст нам искомую вероятность как функцию времени. Для нахождения определённого состава семейства кривых необходимо задаться распределением вероятностей состояний системы на заданный момент времени t_зад, чаще всего t_зад = 0. Это распределение получило название вектор - строки вероятностей начальных состояний системы, которые, как и ранее, обозначим (см. лекцию №1.2):

(27)

Структура дифференциального уравнения построена по правилу, которое можно сформулировать следующим образом: левая часть уравнения - производная по времени от интересующего нас события; правая часть - алгебраическая сумма произведений вероятностей состояний системы на соответствующие интенсивности; со знаком "+" для стрелок, входящих в данное состояние и со знаком "-" для стрелок, выходящих из данного состояния.

Это правило составления дифференциальных уравнений является общим и справедливо для любой непрерывной Марковской цепи.

Таким образом, можно сделать следующие выводы, что:

1. Математической моделью НЦМ является система дифференциальных уравнений (СДУ), т.к. состояние системы А_k взято нами произвольно.

2. Число дифференциальных уравнений равно числу неизвестных, но, чтобы эту СДУ разрешить, необходимо использовать дисциплинирующее условие:

(28)

т.е. в любой момент времени система должна быть в одном из состояний.

3. Решается СДУ методами численного интегрирования (например: методом Рунге-Кутта - при постоянном или переменном шаге интегрирования).