2. Разработка математической модели

Систему эксплуатации автомобиля в установившемся режиме представим в виде матрицы:

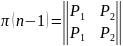(35)

Так как n   , то

(36)

Элементы результирующей матрицы представляют собой систему однородную линейных алгебраических уравнений:

1. Для автомобиля марки А:

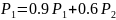(37)

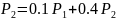
Добавим к этим уравнениям условие нормировки:

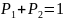
2. Для автомобиля марки В:

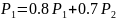(38)

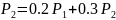
Добавим к этим уравнениям условие нормировки:

3. Расчёт показателя эффективности

Решив полученную систему однородных линейных алгебраических уравнений с использованием математического пакета MathCAD получаем следующие результаты:

1. Д 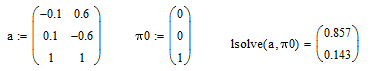ля автомобиля марки А:

2. Для автомобиля марки В:

4 . Анализ полученных результатов

Автомобиль марки А наиболее предпочтителен для приобретения в личное пользование.

Заключение

Таким образом, при разработке математической модели динамики действий целесообразно придерживаться следующей последовательности:

1. Определить:

• основной и дополнительный показатель эффективности;

• возможные состояния системы;

• шаг процесса;

1. Указать класс ДЦМ.

2. Построить граф-процесса.

3. Определить вероятности перехода для каждого шага процесса.

4. Разработать матрицы вероятностей переходов для каждого шага процесса.

5. Определить начальное состояние системы.

6. Выбрать типы формульных зависимостей расчёта ПЭ.

7. Определить формы выдачи результатов математического моделирования.

8. Произвести:

• оперативно-тактические расчёты на ПЭВМ с использованием имеемого программного обеспечения, прикладного математического пакета «MathCAD», или электронно-вычислительных таблиц «Excel» из пакета «Microsoft Office».

• анализ результатов математического моделирования и выработать предложения.

Литература

1. Основная:

1. Бабурин В.А., Полянская Т.И., Шилкина И.Д., Экономико-математические методы и модели в управлении водным транспортом: Системы массового обслуживания: Учебное пособие. СПб.: СПГУВК, 2009.

2. Вентцель Е.С., Исследование операций: Учебник. М.: Советское радио, 1972.

3. Хэмди А. Таха, Введение в исследование операций: Руководство. М.: Вильямс, 2001.

2. Дополнительная:

4. Вентцель Е.С., Теория вероятностей: Учебник. М.: Наука, 1964.

ЛЕКЦИЯ № 1.2

ТЕМА 3. МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ МЕТОДОМ НЕПРЕРЫВНЫХ ЦЕПЕЙ МАРКОВА

Основные вопросы лекции:

1. Потоки событий.

2. Особенности моделирования экономических процессов методом непрерывных цепей Маркова.

3. Математические модели систем массового обслуживания.

Введение

Актуальность темы

При количественном обосновании поиск решения поставленной задачи осуществляется с использованием математической модели исследуемого процесса Одним из основных инструментов при разработке вероятностных моделей вариантов действий являются Марковские цепи.

Подведение к основной мысли

На практике значительно чаще встречаются ситуации, когда переходы системы из состояния в состояние осуществляются в любые моменты времени, которые заранее указать невозможно. Математическая модель таких случайных процессов формируется методами теории непрерывных цепей Маркова (НЦМ), которую мы ранее разделили на два больших класса (см. лекцию 1.1.):

• система массового обслуживания (СМО);

• процессы поиска (ПП).