
- •2. Особенности содержания экономико-математической постановки задачи на моделирование действий с использованием метода дискретных цепей маркова
- •3. Методы разработки математических моделей дискретных цепей маркова
- •3.1 Математическая формулировка задачи
- •3.2 Модели дцм с конечным числом шагов
- •1. Уяснение эмпз
- •2. Разработка математической модели
- •3. Расчёт показателя эффективности
- •3.3 Модели дцм с бесконечным числом шагов
- •2. Разработка математической модели
- •3. Расчёт показателя эффективности
- •4 . Анализ полученных результатов
- •Заключение
- •Литература
- •Основная:
- •Дополнительная:
- •Введение
- •Конкретная цель
- •Основная часть
- •1. Потоки событий
- •2. Особенности моделирования экономических процессов методом непрерывных цепей маркова
- •3.1. Особенности моделирования экономических процессов с применением теории систем массового обслуживания
- •3.2. Математические модели систем массового обслуживания
- •Литература
- •Основная:
- •Дополнительная:
1. Уяснение эмпз
Цель действий: Определить марку автомобиля, являющуюся более предпочтительной для приобретения в личное пользование.
Показатель эффективности: Вероятность нахождения автомобиля в исправном состоянии.
Цель математического моделирование: Определение вероятности состояний для каждой марки автомобиля после k лет эксплуатации.
2. Разработка математической модели
Представим процесс эксплуатации автомобилей в виде системы. Состояния системы характеризоваться исправностью автомобиля в период эксплуатации. Исходя из этого система может находиться в одном из двух состояний:
- S1 – автомобиль исправен;
- S2 – автомобиль требует ремонта;
Состояние системы меняется в фиксированные моменты времени через месяц, 3 месяца и 5 месяцев. Поэтому процесс эксплуатации автомобилей может быть представлен как дискретная цепь Маркова (Марковский случайный процесс с дискретным числом состояний системы и дискретным временем переходов).
Граф-процесса данной системы можно представить в следующем виде:
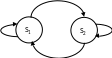
Рисунок 4. – Граф-процесса системы эксплуатация автомобиля
Тогда матрица переходов за один шаг процесса будет иметь вид:
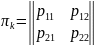 (24)
(24)
Начальное состояние системы спроса на горюче-смазочные материалы зададим вектором строкой:
 (25)
(25)
Через месяц спрос на горюче-смазочные материалы составит:
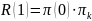 (26)
(26)
Через 3 месяца спрос на горюче-смазочные материалы составит:
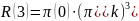 (27)
(27)
Через 5 месяца спрос на горюче-смазочные материалы составит:
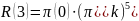 (28)
(28)
3. Расчёт показателя эффективности
Для автомобиля марки А.

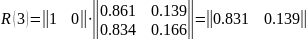

Для автомобиля марки В.
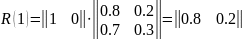
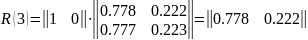

3.3 Модели дцм с бесконечным числом шагов
Режим
работы системы при достаточно большом
числе шагов k является стационарным
(установившемся). В установившемся
режиме система S случайным образом
меняет свои состояния, но вероятность
каждого из них постоянна и не зависит
от времени. До наступления стационарного
режима система находиться в переходном
режиме, длительность которого можно
определить с помощью некоторого
показателя, зависящего от разности
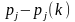 .
.
Однородная дискретная цепь Маркова называется эргодической, если она обладает следующими свойствами:
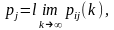 при
при
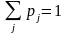 ,
где
,
где
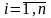 ,
,
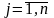
 (29)
(29)
где pij(k) – вероятность перехода из состояния Si в состояние Sj за k шагов;
рj – можно рассматривать как вероятность того, что система окажется в состоянии Sj на k шаге, если k стремиться к бесконечности, поэтому данные вероятности называются предельными (финальными) вероятностями.
Наиболее важной задачей для эргодических цепей является вычисление предельных вероятностей, если известно начальное распределение системы и матрица переходных вероятностей. Из формулы полной вероятности следует, что
 (30)
(30)
Но
для установившего режима безусловные
вероятности рj(k)
равны вероятностям состояний системы
 ,
которые при
,
которые при
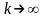 стремятся к предельным вероятностям
рj.
стремятся к предельным вероятностям
рj.
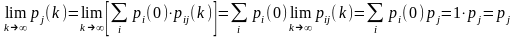 (31)
(31)
Поэтому получили однородную систему линейных алгебраических уравнений
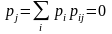 (32)
(32)
Добавив к ней условие нормировки
(33)
и решая систему (27) и (28) различными методами (например, по формулам КРАМЕРА, или ГАУСА) находят предельные вероятности.
Обозначим
вектор предельных вероятностей как
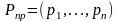 .
Тогда систему алгебраических
линейных уравнений можно записать в
матричной форме
.
Тогда систему алгебраических
линейных уравнений можно записать в
матричной форме

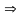
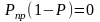 (34)
(34)
Если начальные вероятности состояний системы совпадают с предельными вероятностями, то во все моменты времени система находиться в стационарном режиме.
Если дискретная цепь Маркова содержит хоть одно поглощающее состояние, то она называется поглощающей. Основная особенность поглощающих цепей заключается в том, что вероятность перехода в любое несущественное состояние при числе шагов стремиться к нулю, а вероятность перехода в поглощающие состояния стремиться к единице. Поэтому поглощающие состояния иногда ещё называют предельными.
Пример №4.
Определить спрос в процентном отношении на горюче-смазочные материалы различных фирм производителей в установившемся режиме, считая, что частости смены горюче-смазочных материалов различных фирм производителей останутся неизменными? Исходные данные представлены в примере №4.
