2. 3.2 Модели дцм с конечным числом шагов

Вероятности переходов системы p_ij(k) после k-го шага определяются рекуррентным уравнением Колмогорова-Чепмена:

(i=1, 2,…n; k1) (9)

а вероятности состояний системы = р_i после k-го шага определяются, как для:

• однородной ДМЦ

(i=1, 2,…n; k1) (10)

• неоднородной ДЦМ

(i=1, 2,…n; k1) (11)

Соответственно для матрицы вероятностей переходов (k) за k шагов справедливо выражение:

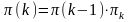(12)

Тогда матрица вероятностей переходов за k шагов определяется в результате последовательного матричного перемножения n k-ых матриц:

(13)

Матрица переходов за k шагов обладает теми же свойствами, что и матрица переходов за один шаг. Таким образом, для однородной цепи Маркова:

(14)

Произведение матриц вероятностей переходов за один шаг неоднородной цепи Маркова не удовлетворяет закону коммутативности. Для любых , где K множество матриц переходов за один шаг, справедливо условие:

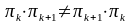(15)

Это обстоятельство позволяет использовать аппарат цепей Маркова с дискретным параметром для обоснования последовательности действий для решения поставленных задач.

Однако для того, что бы определить вероятность нахождения системы в том и ином состоянии за один или несколько шагов, необходимо знать в каком состоянии находилась система перед первым шагом, т.е. её начальное состояние.

Начальное состояние системы задаётся распределением вероятностей её состояния (i=1, 2, …, n), которое определяется на основании результатов уяснения задачи и оценки среды. Это распределение задаётся в виде вектора-строки

= (p₁⁽⁰⁾, p₂⁽⁰⁾,…, p_n⁽⁰⁾) (16)

или же матрицы переходов (0), у которой элементы одной строки являются распределением, а элементы всех других строк равны нулю.

Тогда вероятности состояний системы S за k шагов с учётом её начального состояния определяются по формуле:

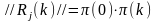(17)

Знание распределения вероятностей состояний системы за k шагов позволяет найти интересующие нас показатели эффективности I –го и II-го типов:

• Вероятность достижения цели действий за заданное число шагов k процесса определяется по формуле:

(18)

где А_r – множество целевых состояний системы, переход в которые означает достижение цели действия сил.

• Вероятность достижения цели действий на k-м шаге процесса определяется по формуле:

(19)

• Математическое ожидание достижения цели действий за заданное число k шагов процесса определяется по формуле:

(20)

где В_j(k) – получаемая выгода при переходе системы за k шагов процесса.

• Математическое ожидание числа шагов процесса, необходимых для достижения цели действия определяется по формуле:

(21)

• Математическое ожидание времени за k шагов процесса, необходимых для достижения цели действия, определяется по формуле:

(22)

где 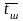– математическое ожидание промежутка времени между очередными шагами процесса;

Вычисление значений основного показателя эффективности и других параметров определяются количеством вариантов последовательности действий через варианты матричного перемножения, число которых определяется выражением:

(23)

где N_в – число вариантов последовательности действий;

n – число типов действий;

а, в, … – числа одинаковых шагов процесса для каждого типа действий.

Пример №4.

Магазин продаёт две марки автомобилей A и B. Сбор статистических данных опыта эксплуатации этих марок автомобилей позволил определить различные переходные вероятности, соответствующие состояниям «исправен» и «требует ремонта». Элементы матрицы перехода определены на годовой период эксплуатации автомобиля соответственно.

Требуется найти вероятности состояний для каждой марки автомобиля после k лет эксплуатации, если начальное состояние соответствует тому, что автомобиль исправен, а также определить марку автомобиля, являющуюся более предпочтительной для приобретения в личное пользование на основе оценки предельных вероятностей состояний автомобиля?

Таблица 1. – Исходные данные

Марка автомобиля	Матрицы вероятностей переходов состояний системы		Срок Эксплуатации, год
А	0.9	0.1	к1	1
	0.6	0.4	к2	3
В	0.8	0.2	к3	5
	0.7	0.3