ЛЕКЦИЯ № 1.1

ТЕМА 2. МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ МЕТОДОМ ДИСКРЕТНЫХ ЦЕПЕЙ МАРКОВА

Основные вопросы лекции:

1. Особенности применения методов теории цепей Маркова.

2. Особенности содержания экономическо-математической постановки задачи на моделирование действий с использованием метода дискретных цепей Маркова.

3. Методы разработки математических моделей дискретных цепей Маркова.

ВВЕДЕНИЕ

Актуальность темы

Сложность, динамичность и многообразие действий требуют от руководителей владения современными методами обоснования решений, как при создании транспорта, так и в процессе её применения. В современных условиях на помощь искусству принятия решения, основанному на логическом анализе опыта и интуиции приходит дополнительное средство в виде математических методов, разработанных в теории исследования операций. Этот метод призван находить закономерности в выбранных действиях и рассчитывать их эффективность на основе показателей эффективности, что позволяет наиболее полно использовать информацию о реальной среде для обоснования решения.

Подведение к основной мысли

При количественном обосновании поиск решения поставленной задачи осуществляется с использованием математической модели исследуемого процесса. Одним из основных инструментов при разработке вероятностных моделей вариантов действий являются Марковские цепи.

Конкретная цель

В лекции рассмотрим основы теории дискретных цепей Маркова для оценки эффективности действий по управлению водным транспортом.

ОСНОВНАЯ ЧАСТЬ

1. ОСОБЕННОСТИ МОДЕЛИРОВАНИЯ УПРАВЛЕНЧЕСКИХ ПРОЦЕССОВ МЕТОДАМИ ЦЕПЕЙ МАРКОВА

Все действия как объект математического моделирования могут быть представлены в виде системы S, которая может находиться в одном из состояний S_i (где 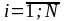). Состояния системы определяются конкретной экономической ситуацией для данных условий среды. В большинстве случаев действия объектов исследования выступают перед руководителем как случайные процессы, протекающие во времени.

Случайными процессами - называются такие процессы, которые при их повторении приводят к различным результатам, причём заранее неизвестным к каким именно [1]. Случайный процесс 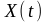можно рассматривать как числовую функцию времени, принимающую различные реализации:

• одномерный случайный процесс

(1)

• многомерный случайный процесс

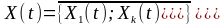(2)

где x(t) - конкретное мгновенное значение случайной величины

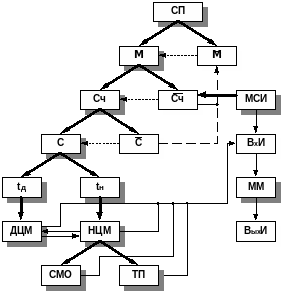
Рисунок 1. – Классификация случайных процессов

Каждый случайный процесс системы обладает той или иной возможностью появления. Тогда численная мера степени объективной возможности появления данного случайного процесса – есть вероятность события P_i(t) [4], а для системы в целом вероятность её состояния .

Для математического описания случайных процессов системы S, в ходе которых она изменяет своё состояние, необходимо включать те её элементы, которые интересуют руководителя при принятии решения. Чем больше элементов и связей между ними включено в понятие система, тем больше возможных её состояний S_i приходиться формулировать.

Если для каждого момента времени t₀ вероятность любого состояния системы S_i в будущем (при t > t₀) зависит только от ее состояния в настоящем S_i (при t= t₀) и не зависит от того, когда и каким образом система пришла в это состояние, то данные случайные процессы, протекающие в системе называются - Марковскими процессами (M). Остальные процессы считаются не Марковскими ( ).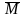

Пример №1

Грузовой район порта, обрабатывают только самоходные грузовые суда. Поступление каждого из них независимо от остальных судов. Для будущего состояния порта не имеет значение, когда обрабатывалась очередь судов на рейде. Важно то, что она есть, что все причалы заняты, что в данный момент у причалов стоят определённые суда с каким-то количеством различных видов груза.

В принципе любой Немарковский случайный процесс может быть представлен как Марковский, за счёт увеличения числа состояний системы, но для этого необходимо сформулировать новые допущения и ограничения.

Марковские случайные процессы делятся на классы, в зависимости от того, как и в какие моменты времени система S может менять своё состояние:

• процессы со счётным (Сч) и с несчётным ( ) множеством состояний системы;

• процессы стационарные (С) и нестационарные ( );

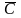• процессы с дискретным (t_д) и непрерывным (t_н) временем переходов системы из состояния в состояние.

В экономической области решения поставленной задачи всегда есть возможность от несчётного числа состояний системы перейти к счётному.

Пример №2

Перечислить скорость движения судна не как числа, а как имеющие определённый смысл – малый ход, средний ход, полный под, экономическая скорость и т.д.

У стационарных случайных процессов вероятностные характеристики не меняются с течением времени, а у нестационарных - вероятностные характеристики являются функцией времени, прошедшего с начала процесса. Математически могут быть описаны оба класса случайных процессов, но всегда можно с помощью допущений и ограничений нестационарные случайные процессы представить как стационарные.

Пример №3

Поток донесений, поступающих в органы управления порта за сутки в общем не стационарный, но рассматривая его за короткий промежуток времени, его можно представить стационарным.

Дискретные случайные процессы – это процессы, которые происходят в фиксированные моменты времени t_д. Непрерывные случайные процессы являются функцией времени при которых переход системы S из состояния в состояние осуществлении в любой, наперёд неизвестный случайный момент времени t_н.

В зависимости от характера представления действий как случайных процессов выбирают методы их математического моделирования: дискретных цепей Маркова, непрерывных цепей Маркова, статистических испытаний.

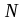Дискретной цепью Маркова − называется случайная Марковская функция со счётным множеством возможных значений случайной величины (где , - число состояний системы), характеризующаяся состояниями системы объекта исследования, изменяющимися в фиксированные моменты времени 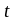с некоторой вероятностью p_i.

Непрерывной цепью Маркова − называется случайная Марковская функция со счётным множеством возможных значений случайной величины (где , - число состояний системы), характеризующаяся состояниями системы объекта исследования, изменяющимися в непрерывные моменты времени с некоторой вероятностью p_i [2, с. 194]. Непрерывная цепь Маркова применяется для описания процессов в системах массового обслуживания, а также поисковых действий.

Таким образом, продемонстрирована моделируемость любого случайного процесса действий, интересующего исследователя. Теория Марковских процессов широко используется для построения математических моделей экономических систем, состояние которых зависит от случайных факторов. На водном транспорте к таким системам, прежде всего, относятся порты и судоремонтные предприятия, обслуживающие флот.

2. Особенности содержания экономико-математической постановки задачи на моделирование действий с использованием метода дискретных цепей маркова

Напомню, что моделирование действий выполняется в четыре этапа исследования операций:

• первый этап – формулирование руководителем экономико-математической постановки задачи (ЭМПЗ) на формирование модели предстоящих действий;

• второй этап – разработка математической модели предстоящих действий;

• третий этап – программная реализация математической модели и включение ее в состав специального математического и программного обеспечения комплексов средств автоматизации управления (СМПО КСА), создаваемых на базе ЭВМ (mainframe или ПЭВМ);

• четвёртый этап – расчёт показателей эффективности предстоящих действий с использованием математического моделирования, анализ и использование его результатов. Выработка должностными лицами органа управления рекомендаций по применению ресурсов для принятия решения.

Экономико-математическая постановка задачи должна содержать информацию, позволяющую разработать модель процесса действий с составлением ее структуры и избрать метод математического моделирования. Основой для формулирования ЭМПЗ являются результаты уяснения им поставленной задачи, оценки среды и выработанная основная идея замысла действий:

• цели предстоящих действий;

• что является основным и дополнительным показателем эффективности действий;

• наиболее важные факторы среды, непосредственно влияющие на успешность выполнения поставленной задачи;

• что является системой S;

• каковы возможные состояния системы S_i как полной группы несовместных событий, где , N - число состояний системы);

• что является шагом процесса, и в какие моменты времени осуществляются эти шаги;

• какие переходы системы из состояния S_i в состояние S_j возможны за один шаг процесса, причин, способных вызвать эти переходы, возможное число шагов процесса;

• численные значения основных параметров, необходимых для вычисления вероятностей p_i,j возможных переходов системы из одних ее состояний в другие;

• в определении начальных состояний системы, как информации необходимой для вычисления вероятностей всех возможных состояний системы S при каждом шаге процесса;

• элементы замысла (решения, плана), необходимые для обоснования количественными методами;

• цель математического моделирования;

• перечень ограничений и допущений.

Цель предстоящих действий вырабатывается руководителем или лицом, принимающим решение, как конечный результат, который должен быть достигнут при реализации эффективного варианта предстоящих действий. Она является логическим следствием содержания задачи, поставленной организации¹.

Основной показатель эффективности формулируется руководителем или лицом принимающим решение как семантическое выражение функции от цели действий и возможности получения определённой выгоды или в некоторых случаях причинённого (получаемого) ущерба² и зависит от числа целевых состояний исследуемой системы S:

ОПЭ =F {цель действия, ущерб(выгода)} (3)

Выгода или ущерб определяются, как условие, качественно-количественная характеристика которых, позволяет считать цель достигнутой. Иными словами, определяется, что и в каком количестве должно быть достигнуто в результате предстоящих действий. Целевыми состояниями исследуемой системы S являются те из её состояний S_i, нахождение в которых после k шагов процесса определяют достижение цели действий.

Возможные состояния системы как полной группы несовместных событий и возможные переходы системы из состояния в состояния являются семантическим описанием динамики предстоящих действий (периодов, этапов, ситуаций, эпизодов) с учётом конкретных условий (факторов) среды и начального состояния системы. Данное семантическое описание динамики предстоящих действий должно отражать как организационные, так и пространственно-временные характеристики всех случайных процессов системы.

Цель математического моделирования вырабатывается руководителем или лицом принимающим решение, как результат определения каких элементов замысла необходимо обосновать и какие управляющие параметры, характер влияния которых на эффективность предстоящих действий, необходимо исследовать. Иными словами, указываются от каких управляющих параметров необходимо получить функциональные зависимости³ предстоящих действий.

Принятые допущения и ограничения, с одной стороны, должны в минимальной степени искажать исследуемый процесс в экономической системе, с другой стороны, они должны позволить сформировать относительно простую и наглядную математическую модель.