46 Статикалық сипаттамасы барлық қималарында бірдей болатын кездейсоқ процестерді, кездейсоқ стационарлы процесс деп аталады.

Кездейсоқ  сөзі алдын-ала процестің нақты таралуын болжау мүмкін еместігін көрсетеді. Анықтау бойынша кездейсоқ процесс X(t)-бұл кез-келген t уақыт мезетінде қабылданатын мәндер кездейсоқ шамалар болып табылатын ерекше түрдегі функция. Кездейсоқ процесстің типтік мысалы ретінде қабылдағыш кірісінде Z(Q)=S(t)+N(t) кернеуі жұмыс жасай алады. Берілген мезетте кернеуді бақылай отырып, біз келесі уақыт мезеттерінде ол қандай мәнлерге ие бола алатындығын болжай аламыз. Бұл мынамен  түсіндіріледі: таратушымен қалыптастырылатын арналық каналдың S(t) (амплитуда, жиілік, фаза) параметрлері жіберілетін хабарға a(t) байланысты кездейсоқ өзгеріп отырады.Сонымен бірге, таралу процесінде сигнал кездейсоқ сипатқа ие әртүрлі адетивті бөгеуілдердің N (t) әсеріне шалдығады.Процестің кездейсоқтылығы X(t) бақыланатын функцияның түрі бір бақылаудан басқасына кездейсоқ ауысатындығымен көрсетіледі. Бірақ, әрбір жеке тәжірибеден алынатын X(t)  функцияның шешімі кездейсоқ емес, оны кездейсоқ функцияның таралуы(реализация)деп аталады. Кездейсоқ процесс статикалық ансамбль жасайтын шексіз мұндай таралулардың жиынтығын ұсынады.

Кездейсоқ шама (х₁;х₂) аралығында қандай да бір мәнге ие болу ықтималдығы P( )= ∫ ᴡ(x) dx=1 өрнегімен анықталады.

Басқa х шамасынан асып кетпеу ықтималдығымен анықталатын кездейсоқ Х шамасының маңызды сипаттамасы ИФР  F(x) болып табылады.

ИФР келесі қасиеттерге ие:

а) F(-∞)=0;

б) F(∞)=1;

в) F(x) — шығынсыз функция, яғни х₂ > x₁ кезінде F (x₂) ≥ F (x₁);

г) P[x₁≤X≤x₂]=F(x₂)- F(x₁).

    Кездейсоқ процессті толығырақ сипаттау үшін кездейсоқ процесстің қасиетін сипаттайтын  қималарында  n - өлшемді ықтималдық тығыздығымен w(x₁, x_2,…, x_n; t₁,t_2,…, t_n)  немесе F(x₁, x_2,…, x_n; t₁,t_2,…, t_n) n - өлшемді ИФР t₁,t_2,…, t_n бойынша орналыстыру керек.

        

47Жағдайдың сандық бейнеленуін сәйкес тербелістер вектормен жасау ыңғайлы болады. сигналдар орнына оларға сәйкес векторымен алмастырамыз, ал y(t) векторының орнына

ауыстырамыз.

Байеса теоремасы сүйене отырып

Бөлімі I нөмерінен тәуелсіз болғандықтан, шешімі осылай анықталады

Мұндағы x,s,y көпөлшемді кеңістік, x(t) хабарламаға сәйкес сигнал s(t)=s[x(t),t] кіріс реализациялауына y(t)=s(t)+n(t) сәйкес болуы керек.

Дискретті хабарламалардың оптималды қабылдағышы қате шешім беруі мүмкіндігіне қарамастан өзге қабылдағыштарға қарағанда ықтималдылығы аз.Зерттеушілердің айтуынша алгоритм құрымдық реализация түріне ыңғайлы болып келуі мүмкін және оптималды қабылдағыштардың құрылымдық сұлбасын жасауға және бөгеуілтөзімділікті есептеуге қолданылады.

48 Радиотехникалық құрылғыда маңызды рөлді кездейсоқ процестердің маңызды классы спектральді тығыздығы 0-ден өзгеше болып келетін қуат жатады.Кездейсоқ таржолақты процестің функциясы.

Стационарлы кездейсоқ процесс біржақты қуат спектрі белгілі бір жиілік аралығында шоғырланады. Винера- Хинчина теоремасы бойынша

Жиілік спектр аралығын нолдік спектр аралығына ойша ығыстырсақ

Нөлге жақын аз мөлшері шығыс құрылғыларына сәйкес жойылады.

Мұндағы

функциясын баяу өзгертетін аргумент.

Кездесоқ таржолақты процесс корреляциясының функциясы қуат спектрі орталық жиілікке қатысты симметриялы болған кезде ерекше жай функция болады.

49 сұрақ: Флуктуацияланған фазамен көптеген арналарды (11.3) моделімен сипаттауға болады. Фаза жиі тез флуктуацияланбайды және оның нақты бағасын алу мүмкін болмайды. Сонымен қатар, фаза бағасы кейде күрделі құрылғылардың қолданылуын талап етеді. Сондықтан да егерде келетін сигналдың бастапқы фазасын бағалауға мүмкіндік болса, кейде мұны қабылдамайды және алгоритм қолданады, жорамалмен тұрғызылған, келетін сигналдың бастапқы фазасы белгісіз және (0,2π) интервалында кез-келген мәнді қабылдай алады. Қабылдаудың мұндай тәсілі когерентсіз деп аталады.

         Тиімді когерентсіз қабылдаудың шешімін қабылдау үшін  сигналы үшін шындыққа ұқсас логарифм қатынасынан шығамыз, ол бастапқы фаза нақты белгілі болғанда мына формуламен анықталады

.

         Сигнал үшін көрсетілуді қолдана отырып

,

мұнда   – арна таратудың белгілі коэффициенті, ал – арнадағы кездейсоқ ығысуы,   үшін (  кейін) формуланы былай жазуға болады

      (16.1)

Бұл жерде  әртүрлі  кезінде әртүрлі мән қабылдайтын кездейсоқ шама болып табылады. Шындыққа ұқсас максимум ережесі мұндай жағдайда математикалық күтімі  үлкен болатын шешімінің таңдалуына байланысты.  тапқанда екінші интеграл оң жақта (16.1) -ге тәуелді емес және арна кірісінде сигналының квадраты болып табылады, фаза бойынша -ге ығысқан, ол оның энергиясына әсер етпейді. Осылайша,  екендігін ескере отырып, белгілеулер енгізіп

; ,

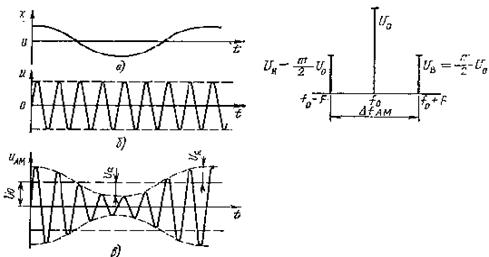
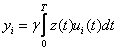                       және  ,             (16.2)

 – 0-ші ретті модификацияланған Бессел функциясы.

         Шындыққа ұқсас қатысты салыстырудың орнына, олардың логарифмдерін салыстыруға болады, ал ол сигналдың екілік жүйесі үшін тиімді когерентсіз қабылдаудың келесі ережесіне алып келеді

                                             (16.3)

бұл теңсіздікті орындау кезінде 1 қабылданады, қарама-қарсы  жағдайда – 0.

50 сұрақ: Амплитудалық модуляция амплитуда тасымалдаушысының өзгерісінің  x(t) бірінші сигналына пропорционал болады.

 гармоникалық сигналының қарапайым жағдайында амплитуда

                             .                        (7.1)

Қорытындысында АМ тербелісті аламыз.

                         .         (7.2)

 

          7.1  Сурет - x(t) және  тербелістерінің графиктері

7.1 суретте x(t) және  тербелістерінің графиктері бейнеленген. Орама АМ тербелісі (7.1) өрнекке сәйкес келеді.  Амплитудасының –ден максимальді өзгерісі орама амплитуданы  көрсетеді; (7.1) сәйкес . Орама амплитуданың тасымалдаушысы амплитудағы қатынасы, модуляция коэффициенті деп аталынады.

                   .                                       (7.3)

Қарапайым жағдайда . Процент түрінде көрсетілген модуляция коэффициенті яғни M=m*100% модуляция тереңдігі деп аталынады. Модуляция коэффициенті модульдеуші сигналдың амплитудасына пропорционал.

(7.3) пайдаланып, (7.2) өрнегін мына түрде жазады

            .                           (7.4)

АМ тербелісінің спектрін анықтау үшін (7.4) өрнектегі жақшаны ашамыз

.    (7.5)

(7.5) өрнегіне сәйкес АМ тербелісі, жақын жиіліктегі үш жоғарғы жиілікті гармоникалық тербелістердің қосындысы болып табылады (  н/е )

а) f₀ тасушы жиіліктің U₀ амплитудамен тербелісі;

б) f₀+F жоғарғы  жанама жиіліктің    амплитудамен тербелісі; 

в) f₀-F төменгі жанама жиіліктің  амплитудамен тербелісі.

АМ тербелісінің спектрі (7.5) 7.1 суретте көрсетілген.

51 сұрақ: Ақпараттың жеке саны. Хабардың дискретті көзі а символының тізбегін берді делік. Бұл хабардағы  ақпараттың жеке санына формальды анықтау берейік, келесі талаптарды ескермей:

         а) ақпарат саны  аддитивті функция болуы қажет, яғни   өзара тәуелсіз хабар жұбы үшін ол оның әрқайсысындағы ақпарат санының қосындысына тең болуы керек, яғни  ;