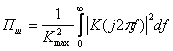2.1 Сурет - Дискретті хабарлар жүйесінің құрылымдық сұлбасы

2.2 Сурет - Дискретті хабарды сигналға түрлендіру процессі

Қазіргі дискретті хабарларды тарату жүйелерінде салыстырмалы өзіндік құрылғылардың екі топтарын  ерекшелеуге болады: кодектер; модемдер.

Кодектер дегеніміз хабарды кодқа (кодер) және кодты хабарға түрлендіретін құрылғыларды атайды. Модем дегеніміз кодты сигналға (модулятор) ал сигналды кодқа (демодулятор) түрлендіретін құрылғыны атайды.

10.Сызықты және сызықсыз арналарда сигналды түрлендіру жүйелі операторлар. Стационарлық және стационарлық емес жүйелер. Сызықты және сызықсыз жүйелер.

Статикалық сипаттамасы барлық қималарында бірдей болатын кездейсоқ процестерді, кездейсоқ стационарлы процесс деп аталады.

Жүйелердің классификациясы олардың математикалық моделінің қасиеттері негізінде жүргізіледі. Егер жүйенің шығыс реакциясы, қай уақыт мезетінде кіріс сигналдың түскеніне байланысты болмаса, стационарлы деп аталады. Егер Т стационарлы жүйенің операторы болса,

онда кез келген мәнінде. Сонымен бірге стационарлы жүйелерді уақыт бойынша тұрақты параметрлі жүйелер деп те атайды. Егер жүйенің қасиеті алғашқы уақыт есебін таңдағанға инварлантты болмаса, онда мұндай жүйені стационарлы емес деп атайды (уақыт бойынша айнымалы параметрлермен немесе параметрлі жүйені).

Жүйенің ең маңызды классификациясы мынаған негізделген: кіріске бірнеше сигналдардың қосындысын бергенде, әртүрлі жүйелер әрқилы болады. Егер опрератор жүйесі осындай болса, онда теңдік былай болады:

 мұнда, туынды сан, онда берілген жүйе сызықты деп аталады. M=∆φ_max=aX шарт суперпозициялық функционалды принципін көрсетеді. Егер бұл шарт орындалмаса, онда жүйе  сызықсыз.

11. Үзіліссіз хабардың цифрлық кодтау.

Үздіксіз хабарды цифрлық кодттау үшін алдымен хабарды дискреттеу қажет. Үздіксіз функцияның оның лездік мәндерінің санау негізіндегі ауыстыруының  амалы дискреттелу деп аталады. Яғни үздіксіз хабарды біз үздіксіз функция деп аламыз. Еркін үздіксіз функция   ның дәл елестетілуі үшін соңғы уақыт интервалы  да интервалдың барлық нүктелерінде , яғни бір бірінен шексіз аз интервада орналасқан үздіксіз есептеу көптігі арқылы лездік мәндер туралы деректерді басқару қажет.  функциясы туралы кейбір жақындатылған түсінікті оның  интервалдарында  санақ деп аталатын  мәндеріне ие дискретті импульс кезектері түріндегі бейнеленуі бойынша құруға болады.

6.1 Сурет – Үздіксіз функцияның дискреттелу жиілігі болатын периодикалық коммутацияның негізінде дискреттелуі

Дискреттелу болғаннан кейін хабарды кодтауға болады. Яғни дискертті хабарды кодты символдар (таңба) тізіміне түрлендіреміз.

12. Детерминирленген сызықты арнадағы кездейсоқ сигналды түрлендіру. Шуылдық жолақ. Кең спектрі кездейсоқ сигналдың таржолақты тізбектерден өту.

Финитнамен тұрақты детерминерленген сызықты жүйеде, яғни  уақыт бойынша    0……..  аралығымен шектелген  олардың g(t)

     .         

    дискреттеу қадамын кіріс процессінің   1/F_x   корреляция интервалына тең деп алуға болады. ∆F тар өткізу жолағы білдіреді: τ импульстік сипаттаманың     ұзақтығы ∆τ  салыстырғанда үлкен. Y(t) шығыс процессінің   кез-келген t уақыт мезетіндегі қимасы   сәйкес қосындының N қосылғышымен анықталады. Бұл қосымдылығы өзара коррелирленбеген   процессінің X(t) қималары жатады. Мұндай қосындының ықтималдығының таралуы ықтималдық теориясының орталық шектік теоремасы Гаус теоремасына (жақын болған сайын, Nкөп,    Fx/∆F анықталатын) жақын. Шектеулі жағдайда, егер спектр ені шексіз (уақыт бойыншы сәйкес келмейтін корреленбеген) арна кірісіне ақ шу әсер етсе, ал арнаның өткізу жолағы шектеулі болса, онда    және шығыс процессі   қатаң түрде гаусстық болады. Белгіленген сызықтық арнаның қасиеті сақталады және арна параметрлері өзгергенде де.

Шығыс тұрақты процесстің ФК-ы:

Y(t) .

         Көп жағдайда кең жолақты кездейсоқ сигналдардың сызықты жиілікті іріктеулі тізбектеріне әсерін қарастыру қажет. Мысалы, қысқа импульстардың хаостық тізбектілі әсерінен пайда болатын бұл жағдайда егер кіріс кездейсоқ  процесстің спектрінің тиімді ені жүйенің өткізу жолағының енінен көп болса, онда реалды кездейсоқ процессте оған эквивалентті біржақты спектр қуаты  N₀ = N_x (f₀),  болатын ақ шумен ауыстыруға болады, бұл жерде   f₀ ~  өткізу жолағы аралығындағы кейбір нүкте.

         Инженерлік есептеулерде сызықты жиілікті іріктеулі тізбекті кең жолақта кездейсоқ сигнал әсерінде болатын, шулық өткізу жолағымен     сипаттауға ыңғайлы. Ол реалды тізбектің тарату коэффициентінің модулінің максимумына тең болатын, идеалды жолақты сүзгінің  таратудың заттық коэффициенті болатын өткізу жолағы сияқты анықталанылады: