
- •Сигналдардың кездейсоқ байланыс арналарынан өтуі. Кездейсоқ сызықты арна.
- •Ақпарат, хабар, ақпарат алушы және жіберуші.
- •Бұрыштық модуляция кезіндегі спектрлік тербеліс.
- •2.1 Сурет - Дискретті хабарлар жүйесінің құрылымдық сұлбасы
- •10.Сызықты және сызықсыз арналарда сигналды түрлендіру жүйелі операторлар. Стационарлық және стационарлық емес жүйелер. Сызықты және сызықсыз жүйелер.
- •11. Үзіліссіз хабардың цифрлық кодтау.
- •6.1 Сурет – Үздіксіз функцияның дискреттелу жиілігі болатын периодикалық коммутацияның негізінде дискреттелуі
- •12. Детерминирленген сызықты арнадағы кездейсоқ сигналды түрлендіру. Шуылдық жолақ. Кең спектрі кездейсоқ сигналдың таржолақты тізбектерден өту.
- •13.Сигналдың динамикалық көрінісі.Динамикалық көрініс принципі.
- •14.Бұрыштық модуляция кезіндегі тербеліс.
- •15.Жиіліктік модуляция. Дельта функциясы.Дельта функциясы арқылы сигналдың динамикалық көрінісі.
- •8.4 Сурет
- •19. Фазалық модуляцияны детекторлау
- •20. Ам, жм және фм ның кедергі тұрақтылығы
- •21. Периодты сигналдың спектрлік диаграммасы
- •36) Экспоненциальды бейнеимпульстің спектрлік тығыздығы
- •37) Жадысы бар дискретті арналар модельдері
- •38) Импульс ұзақтығы мен спектр кеңдігінің арасындағы байланыс
- •39) Дискретті арнаның үзіліссіз модельдері
- •41) Дискретті хабарларды қабылдау ережелері мен сапа критерийлері
- •44. Уакыт бойынша сигналдарды дискреттеу. Котельников катары туриндеги жиликтик жолакты сигналдын кориниси
- •45. Келісілген фильтрмен тиімді қабылдағыш
- •45.2 Сурет
- •16.2 Сурет– Квадраттық сұлба
- •17.1 Сурет
- •17.2 Сурет - Кодтық арақашықтықтың және ға байланыстылығы
17.2 Сурет - Кодтық арақашықтықтың және ға байланыстылығы
tи дейінгі барлық қателерді жөндеу мүмкіндігі
![]() .
(17.10)
.
(17.10)
Код
t![]() рет
қателіктерді табу үшін және
рет
қателікті жөндеу үшін кодтық арақашықтық
рет
қателіктерді табу үшін және
рет
қателікті жөндеу үшін кодтық арақашықтық
![]() (17.11)
тең болу керек .
(17.11)
тең болу керек .
R
қосымша разрядтардың саны
кодтық
арақашықтықпен байланысты. Код артық
болған сайын кодтық арақашықтық
та үлкен болады
![]() код
үшін
код
үшін
![]() (17.12)
(17.12)
мұнда Хэммиг коды сызықты жүйелік кодқа қатысты
Ақпараттық разрядтардың сызықты түрлену негізінде тексеруші разряд пайда болады. Тексеруші разрядтарды табу ережесі жөндеуші кодтардың басты шешімі болып табылады. Бұл ережені кейбір сызықты R оператор түрінде анықтаймыз. Қалыптасудың принципиалды екі қалыптасу операторы бар.
![]() (17.13)
(17.13)
![]() (17.14)
(17.14)
Бірінші жағдайда жөндеу бөлігінің bi элементі R {aj} операторымен анықталады. r тексеру разряды табу үшін әр түрлі R операторын r тізбектей қолдану қажет.
Екінші жағдайда R операторы ақпараттық бөліктің барлық разрядына бірдей әсер етеді. Екіші жағдайға циклдық кодтар қатысты. Қатені Хэмминг коды бойынша жөндеу және табу анықтамаға сәйкестендіріледі. Екі қабылданған тексеру элементінің модулі бойынша қосынды жиынтық элементі “синдром” түсінігін береді. Тексеруші топтың элементін қалыптасуымен Хэмминг кодын қарастырады.
![]() табу
үшін таратушы жақта
табу
үшін таратушы жақта![]() операторы қолданылады, мұнда {aj}
берілген кодтық комбинацияның ақпраттық
элементі .
операторы қолданылады, мұнда {aj}
берілген кодтық комбинацияның ақпраттық
элементі .
Қабылданған
тексеруші элементтер![]() есептеу
бар екі модуль бойынша жазылады.
есептеу
бар екі модуль бойынша жазылады.
![]()
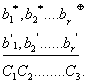 (17.15)
(17.15)
Қосу
қорытындысында кейбір кодтық комбинация
– синдром немесе қате вектор алынады.
Барлық ai дұрыс қабылданды деп
есетейік, сонда
![]() .
Егер тексеруші элементтерді қабылдау
кезінде қате жібермесе, онда
.
Егер тексеруші элементтерді қабылдау
кезінде қате жібермесе, онда
![]() Бұл
жағдайда синдромның разряды:
Бұл
жағдайда синдромның разряды:
![]() нөлдермен
көрсетіледі.
нөлдермен
көрсетіледі.
Егер бұл жерде қате кетсе, онда синдромның құрамында 1 шығады. Бұл Хэмминг коды бойынша қатені анықтау болып табылады.
Хэмминг коды d0=3 минимальді кодтық арақашықтыққа ие. Бұл дегеніміз, код қатені жөндей алады, яғни кодтық комбинациядағы позицияның нөмірін көрсетеді
{Ri} – ді ақпараттық бойынша жөндеу элементін қалыптасу операторымен анықтайық
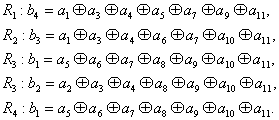 (17.16)
(17.16)
Көрсетілген қатынасты Н тексеру матрицасы түрінде көрсетейік. Ол n бағаннан және r жолдан тұрады. Ақпараттық элементтердің номері, яғни қосындыға қатысады, бірлікпен анықталады. Тексеруші элементтер Ei бірлік матрицасы түрінде көрсетіледі. (9.5) Қарастырылатын код үшін
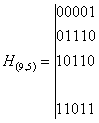
![]()
![]() ,
,
![]() (17.17)
(17.17)
(17.17)
– де пунктермен Er
бірлік
матрицасы көрсетілген. Бірінші жолдан
b1-ді
қалыптастыру үшін a5:b1=a5
элементін алу қажет. 2 жолдан
![]() .
Сәйкесінше, 3 және 4 жолдан
.
Сәйкесінше, 3 және 4 жолдан
![]() ;
;![]() .
.
