16 Вопрос Плоская волна в поглощающей среде

Ограничимся рассмотрением прямой волны (для простоты письма индекс "+" опустим). В этом случае ,

кроме того, .

Рассмотрим линейно-поляризованную волну. При этом

(2.13)

,

причём , ,

Положим , тогда ,

(2.14)

П

(2.15)

редставим в виде тогда вектор определится:

где – коэффициент затухания.

Выражения (2.14) и (2.15) показывают:

5. распространяющаяся в поглощающей среде плоская волна затухает по экспоненциальному закону;

6. векторы и взаимно перпендикулярны и лежат в плоскости, перпендикулярной направлению распространения волны;

7. волна распространяется с постоянной фазовой скоростью .

Длина волны в поглощающей среде равна:

Следовательно, ;

8. в отличие от идеальной среды колебания векторов и во времени в поглощающей среде происходят со сдвигом фаз на угол . Этот сдвиг фаз появился, вследствие того, что характеристическое сопротивление – величина комплексная.

Определим и через параметры среды и частоту:

В начале определим :

Следовательно,

Здесь

(2.16)

;

Но

В результате

(2.17)

,

где – коэффициент затухания

– фазовый коэффициент.

.

С другой стороны, . Следовательно,

(2.18)

,

Из выражений (2.14) и (2.15) следует, что составляющие поля электромагнитной волны для идеальной непоглощающей среды получаются как частный случай этих выражений при . Так при получаем , , , , .

Особенностью волны, распространяющейся в поглощающей среде, является то, что основные её параметры: фазовая скорость, коэффициент затухания, характеристическое сопротивление зависят не только от параметров среды, но и от частоты. Причём зависимость эта довольно сложная, и на практике она сказывается существенно.

Так, если сигнал не является чисто гармоническим, то он, как правило, может быть представлен в виде суммы гармонических колебаний. В результате каждая гармоника будет иметь затухание, свою фазовую скорость и т. д. и поэтому при прохождении некоторого расстояния суммарный сигнал будет искажён.

Вычислим среднюю мощность потерь (потери в единицу времени и в единице объема):

(2.19)

В ычислим среднее значение вектора Умова – Пойнтинга. Этот вектор нужно знать для вычисления мощности, переносимой волной:

(2.20)

Здесь использовано известное векторное тождество

.

Рассмотрим случай

^.

Этот случай соответствует проводникам, для которых порядка 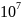См/м. В этом случае ток смещения значительно меньше тока проводимости.

При этом

^{, .}

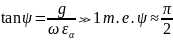Колебания вектора будут отставать от на :

;

.

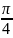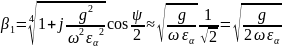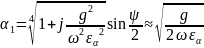Тогда

;

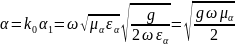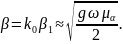
(2.22)

Величина, обратная , есть скин-слой:

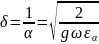
(2.23)

.

Найдём фазовую скорость волны:

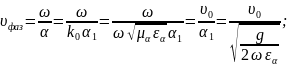
(2.24)

Или .

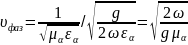Из (2.24) видим, что .

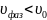Таким образом, в данном случае основные параметры распро­страняющейся волны будут функциями частоты. Фазовая скорость при этом значительно меньше скорости света в диэлектрической среде с такими же , . Следовательно, при той же частоте длина волны в такой проводящей среде будет короче, чем в диэлектрике с параметрами , , так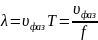 ,