Указание

Область интегрирования ограничена концентрическими сферами, поэтому удобно перейти к сферическим координатам.

Решение

Перейдем к сферическим координатам:

При этом область интегрирования определяется условиями:

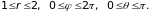
Тогда

Ответ:

III. Криволинейные интегралы

Интегралы, которые мы рассматривали до сих пор, имели своими областями либо отрезки на прямой, либо некоторые области на плоскости и в пространстве.

Теперь рассмотрим случай, когда областью интегрирования является кривая, расположенная в плоскости. Затем все рассуждения можно перенести на случай кривой в пространстве.

Рассмотрение криволинейных интегралов расширяет возможности приложений математического анализа и решения задач физики и техники (и в самой математике – в теории поля и в ТФКП).

Существует два типа криволинейных интегралов. Начнем с рассмотрения криволинейного интеграла, который строится по аналогии с обыкновенным определенным интегралом.

§1. Криволинейные интегралы I типа Определение и свойства криволинейного интеграла I типа

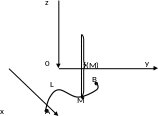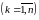Пусть функция z=f(M) определена вдоль некоторой кривой L, лежащей в плоскости XOY, то есть любой точке ML соответствует f(M). Пусть y=(x) - уравнение кривой L, где (x) - непрерывно-дифференцируемая функция. Тогда кривая L будет гладкой и спрямляемой. A, B- концы кривой L. Разобьем кривую произвольным образом на n частей точками A =M₀, M₁,…, M_n=B. На каждой частичной дуге выберем произвольно точку . Составим сумму

, (1)

где - длина дуги .

Эта сумма называется интегральной суммой для функции z=f(M), заданной на кривой L. Обозначим .

Определение. Если существует конечный предел при 0 интегральной суммы (1), не зависящий ни от способа разбиения кривой L на части, ни от выбора точек , то он называется криволинейным интегралом I типа (или криволинейным интегралом по длине дуги) от функции f(M) по кривой L и обозначается или .

Функция f(M) называется интегрируемой вдоль кривой L.

Свойства криволинейного интеграла I типа

1º. Величина криволинейного интеграла не зависит от направления интегрирования:

(это объясняется тем, что при составлении интегральной суммы (1) нумерация точек разбиения может быть произведена и в обратном порядке: от В к А, это ничего не меняет).

2º. (Аддитивность)

.

3º. (Линейность)

.

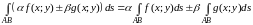2. Задача о площади цилиндрической поверхности

Как известно, определенный интеграл геометрически представляет собой площадь криволинейной трапеции, ограниченной кривой y=f(x), осью 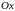и прямыми x=a, x=b. Если f(x)0, площадь надо взять со знаком «-». Аналогично можно прийти к геометрическому смыслу криволинейного интеграла I типа.

Пусть в плоскости дана спрямляемая кривая L=АВ, на которой определена функция f(M)0. Тогда точки (M; f(M)) образуют некоторую кривую, которая лежит на цилиндрической поверхности с направляющей L и образующей, параллельной .

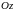Задача. Определить площадь части цилиндрической поверхности, которая ограничена сверху кривой z=f(M), снизу – кривой L, с боков – прямыми AA и BB.

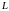Д ля решения этой задачи разобьем кривую произвольно точками A=M₀, M₁,…, M_n=B на n частей. На каждой частичной дуге выберем произвольно точку . Из каждой точки дробления проведем прямые, параллельные оси . Поверхность разобьется на n полосок 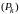. Каждую такую полоску заменим прямоугольником с основанием = и высотой . Площадь ее 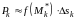. Тогда

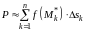. (2)

Равенство (2) тем точнее, чем мельче разбиение кривой L на части. Пусть . Тогда переходя к в (2), получим точное равенство:

.