8. Нахождение функции по её полному дифференциалу

П усть на односвязной области (D) выполнено = . Тогда на этой области дифференциальное выражение Pdx+Qdy является полным дифференциалом некоторой функции F, т.е. dF=Pdx+Qdy. Из сказанного следует, что общий вид таких функций F:

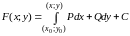. (7)

Интеграл в (7) не зависит от пути интегрирования на области (D). В качестве пути интегрирования возьмем ломаную с двумя звеньями, параллельными осям координат (ACB, ADB):

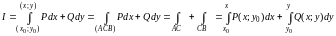.(8)

С другой стороны,

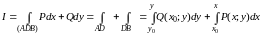. (9)

Из (8), (9), (7) получаем формулы для F:

,

.

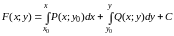Пример. Выяснить, является ли выражение полным дифференциалом некоторой функции, и, если является, найти эту функцию.

Δ P(x;y)= , Q(x;y)= ,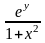

= , = = .

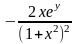Т.к. P, Q, , непрерывны на , и на = , то данное выражение является полным дифференциалом некоторой функции F(x;y) и

.

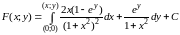(В качестве (x₀;y₀) можно брать любую точку из области непрерывности функций P, Q, , , поэтому возьмем (0;0)).

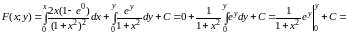
. Δ